4.2. Логическое умножение, конъюнкция, элемент «и»
В алгебре логики операция логического умножения (английское сокращенное обозначение «AND») обозначается символом умножить «·», например, А∙В=Q.
На рис.16. показана электрическая схема, иллюстрирующая работу элемента логического сложения.
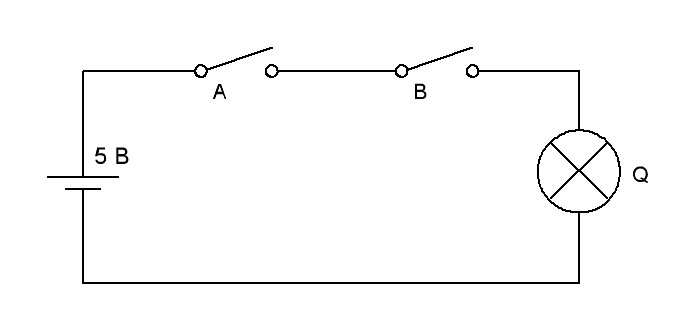
Рис.16. Электрическая схема электромеханического эквивалента логического элемента 2-И
Из схемы следует, что если хотя бы один ключ А или В или оба ключа разомкнуты, то лампочка Q не горит. И только когда оба ключа замкнуты лампочка горит. Эти рассуждения в формальном виде можно представить в виде таблицы истинности для логического элемента 2-И. Цифра «2» в обозначении указывает на то, что в операции логического умножения участвует два сомножителя (в примере А и В). Табл.4 будет иметь три столбца (А, В и Q) и количество строк (за исключением заголовка таблицы), равное 22. Рассмотренную операцию можно записать в алгебраической форме следующим образом: А∙В=Q.
Таблица 4
В |
А |
Q |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Если в схеме рис.16 добавить еще один ключ С (рис.17), то правила работы схемы не изменятся. Разница будет заключатся в том, что лампочка Q будет гореть только тогда, когда все три ключа замкнуты. Таким образом, мы получим логический элемент 3-И. Добавлять ключи можно сколь угодно много, при этом очевидно общее правило работы схемы не изменится.
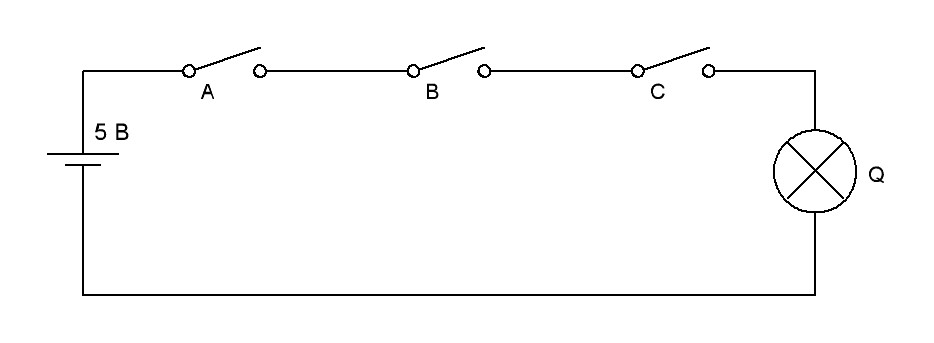
Рис.17. Электрическая схема электромеханического эквивалента логического элемента 3-И
Таблица истинности для логического элемента 3-И будет состоять из четырех столбцов и иметь 23=8 строк (табл.5).
Таблица 5
С |
В |
А |
Q |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Промышленность выпускает четыре типа элементов логического умножения: 2-И, 3-И, 4-И и 8-И. На схемах электрических принципиальных эти элементы изображают, как показано на рис.18.
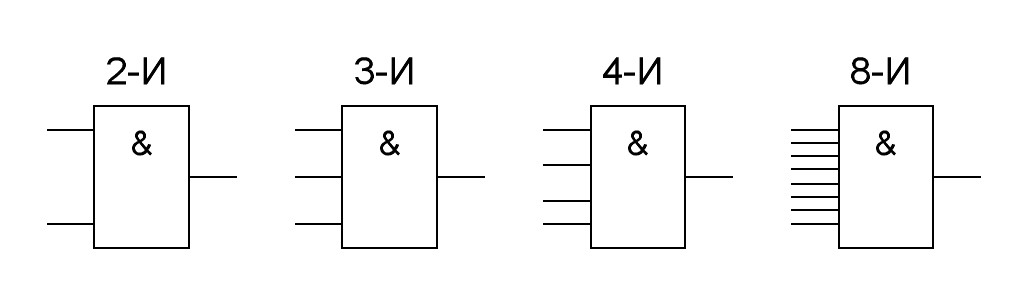
Рис.18. Условное обозначение элементов логического умножения на схемах электрических принципиальных
Построим диаграмму состояний (рис.19) для логического элемента 3-И.
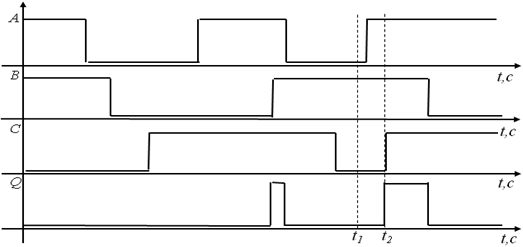
Рис.19. Диаграмма состояний для элемента 3-И
Для этого, также как и в предыдущем случае, зададимся значениями входных переменных А(t), В(t) и С(t) и в соответствии с табл.5 построим на графике значение выходной переменной Q(t). Например, в момент времени t1 A=0, B=1, C=0, в соответствии с значением третьей строки в табл.5 Q=0. Далее в момент времени t2 A=1, B=1, C=1 и в соответствии с значением восьмой строки в табл.5 Q=1.
4.3. Логический элемент «ИЛИ – исключающее»
Для обозначения этой операции в алгебре логики используют символ . Например, АВ=Q. Часто для него используют английское сокращение «XOR».
Проиллюстрировать работу этого элемента с помощью механических ключей и лампочки невозможно, поэтому здесь просто необходимо знать таблицу истинности.
В табл.6 приведена таблица истинности для логического элемента 2-ИЛИ ИСКЛЮЧАЮЩЕЕ.
Таблица 6
В |
А |
Q |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
В табл.7 приведена таблица истинности для логического элемента 3-ИЛИ ИСКЛЮЧАЮЩЕЕ.
Таблица 7
С |
В |
А |
Q |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
Продолжение табл.7
1 |
2 |
3 |
4 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Промышленность выпускает четыре типа логических элементов ИЛИ ИСКЛЮЧАЮЩЕЕ: 2-ИЛИ ИСКЛЮЧАЮЩЕЕ, 3- ИЛИ ИСКЛЮЧАЮЩЕЕ, 4-ИЛИ ИСКЛЮЧАЮЩЕЕ и 8-ИЛИ ИСКЛЮЧАЮЩЕЕ. На схемах электрических принципиальных эти элементы изображают, как показано на рис.20.
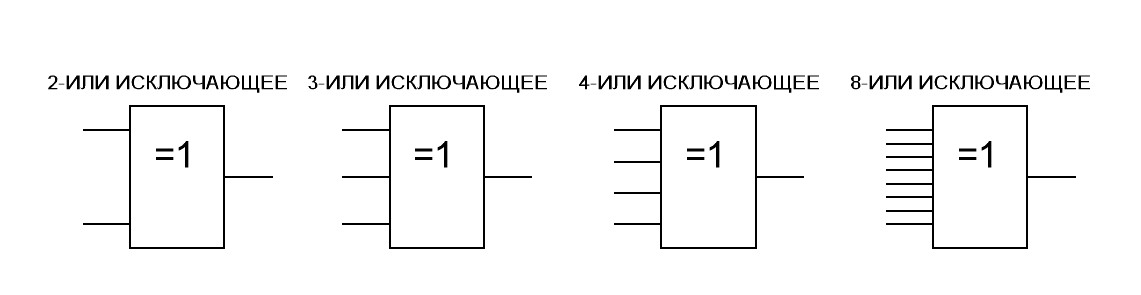
Рис.20. Условное обозначение логических элементов ИЛИ ИСКЛЮЧАЮЩЕЕ на схемах электрических принципиальных
Построим диаграмму состояний (рис.21) для логического элемента 3- ИЛИ ИСКЛЮЧАЮЩЕЕ.
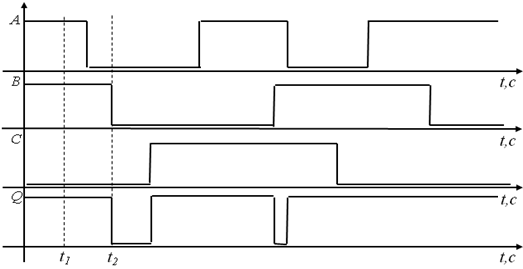
Рис.21. Диаграмма состояний для элемента 3- ИЛИ ИСКЛЮЧАЮЩЕЕ
Для этого, также как и в предыдущих случаях, зададимся значениями входных переменных А(t), В(t) и С(t) и в соответствии с табл.7 построим на графике значение выходной переменной Q(t). Например, в момент времени t1 A=1, B=1, C=0, в соответствии с значением третьей строки в табл.5 Q=1. Далее в момент времени t2 A=0, B=0, C=0 и в соответствии со значением первой строки в табл.7 Q=0.