2. Логические состояния

Под цифровой электроникой понимают такие схемы, для каждой точки которой можно определить, как правило, только два состояния. Обычно в качестве параметра выбирают напряжение, уровень которого может быть «высоким» или «низким» (рис.8). Эти два состояния могут представлять различные биты информации. Например, ключ замкнут или разомкнут, событие произошло либо нет, сигнал присутствует либо отсутствует, уровень аналогового сигнала выше или ниже заданного значения, требуется или не требуется выполнять некоторые действия и т.п. Состояние уровней («высокое» и «низкое»), некоторым заданным образом, определяют «истинное» либо «ложное» значение переменных в алгебре логики (Булева алгебра).

Введем понятие 1 и 0. Эти символы используются в алгебре логики для обозначения утверждения, «истина» и «ложь» соответственно. В электронике 1 и 0 обозначают соответственно «высокий» и «низкий» уровень напряжения. Для различных типов цифровых схем уровень 0 и 1 всегда известны, поэтому нет необходимости обозначать эти уровни абсолютными значениями напряжений.

Например в персональной ЭВМ типа IBM PC, уровень логической 1 соответствует уровню напряжения от 2,4 до 5 В («1» → 2,4 ÷ 5 В), а уровень «0» → 0 ÷ 0,4 В.

2.1. Логические соотношения

Любое обсуждение комбинационной логики будет неполным, если мы не рассмотрим основные логические соотношения. Эти отношения более подробно рассматриваются в таком специфическом разделе математики как «Дискретная математика». Большинство из этих соотношений очевидны, а два последних составляют теорему Моргана, наиболее важную для построения схем. Ниже приведены основные логические соотношения.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. 

18. .

19. .

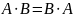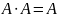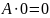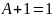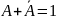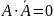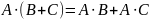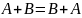3. Системы счисления

Представление данных в ЭВМ, в силу физических законов ее функционирования, не может осуществляться на основе десятичной системы счисления. Базовым элементом любой цифровой ЭВМ является так называемый ключ, поведение которого характеризуется двумя состояниями – включено (1), выключено (0), то есть состояние этого ключа, а также множества других ключей в ЭВМ может быть описано с помощью двух цифр: нуля и единицы. Эти соображения послужили причиной применения двоичной системы счисления.

Все цифры в числе определяются ее порядком. Например, десятичное число 2002,9=210³+010²+010¹+210⁰+910^-1 можно представить в виде суммы частных произведений. Первый сомножитель принимает значение цифры в десятичной системе счисления, а второй – (число десять) основание десятичной системы счисления. Показатель степени при числе 10 равен порядковому номеру позиции цифры в исходном числе.

Для произвольной системы счисления можно записать

kNⁱ+kN^i-1+…+kN¹+kN⁰+kN^-1+…+ kN^-m,

где k – принимает значение любой цифры данной системы счисления; N – основание данной системы счисления; i – номер позиции (показатель степени), которую цифра занимает в числе до запятой, а m – порядковый номер цифры в числе после запятой.

Примеры:

1. _;

2. _;

3. _.

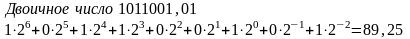С

ущественным недостатком двоичной системы счисления является то, что для представления больших чисел необходимо большое количество двоичных разрядов, а это, в свою очередь, приводит к уменьшению надежности в представлении двоичных чисел. Имеется в виду, что вероятность возникновения ошибки при написании числа с увеличением его разрядности возрастает, кроме того, двоичная система счисления не является компактной. С другой стороны, отказываться от этой системы мы не можем, поэтому в качестве обоснованного компромисса используется шестнадцатеричная система счисления. Ее достоинством является компактность в записи больших чисел и простота при переходе от шестнадцатеричной системы к двоичной и обратно. В табл. 1 в первом столбце показаны десятичные числа от 0 до 15, во втором столбце двоичные эквиваленты этих десятичных чисел, а в третьем столбце приведены цифры шестнадцатеричной системы счисления.

Таблица 1

N(10)	N(2)	N(16)
1	2	3
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9

Продолжение табл. 1

1	2	3
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

Для перехода от двоичной системы счисления к шестнадцатеричной достаточно разбить исходное двоичное число на группы по четыре цифры справа налево и затем заменить эти двоичные группы на соответствующие им цифры шестнадцатеричной системы счисления.

Например:

1. 110.0011.1100.1011.0011₍₂₎ = 63CB3₍₁₆₎;

2. 1111.0000.1010.0111₍₂₎ = F0A7₍₁₆₎;

Обратное преобразование осуществляется заменой шестнадцатеричных цифр в числе соответствующими двоичными эквивалентами из табл. 1.

Например:

2ae7b₍₁₆₎ = 0010.1010.1110.0111.1011₍₂₎.