5. Упрощение логических выражений

Рассмотрим логическое выражение . В процессе составления логической схемы, на основе анализа исходного логического выражения, выясняется, что необходимы один элемент 3-ИЛИ, три элемента 2-И и два элемента НЕ. На рис.32,а изображена схема, реализующая логику заданного выражения.

Входы		Выход
В	А	Q
0	0	0
0	1	1
1	0	1
1	1	1

б)

а)

Рис.32. Упрощение логических выражений: а – логическая схема и б – таблица истинности для логического выражения

На рис.32,б дана таблица истинности для исходного логического выражения и логической схемы. Не трудно увидеть, что приведенная таблица истинности соответствует рассмотренному ранее элементу 2-ИЛИ. Другими словами показанная на рис.32,а схема может быть заменена одним элементом 2-ИЛИ. Или иначе, заданное логическое выражение можно заменить упрощенным

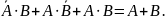
Рассмотренный пример показывает, каким образом необходимо пытаться упрощать исходное логическое выражение, чтобы получить как можно более простую, а, следовательно, более надежную и менее дорогую логическую схему. В приведенном примере видно, что таблица истинности принадлежит элементу 2-ИЛИ. Однако часто приходится использовать более общие методы упрощения логических выражений. Эти методы основаны на приложениях булевой алгебры и построении так называемых карт Карно².

5. Карты Карно

В 1953 г. Морис Карно опубликовал статью о разработанном им методе графического представления и упрощения логических выражений. Карта Карно для двух переменных А и В показана на рис.33.

а)

Таблица истинности

Входы		В ыход
В	А	Q
0	0
0	1
1	0
1	1	Карта Карно

Рис. 33. Обозначение квадратов на карте Карно

Четыре квадрата соответствуют четырем возможным комбинациям А и В в таблице истинности с двумя переменными. При таком изображении квадрат 1 на карте Карно соответствует произведению квадрат 2 – произведению и т.д.

Предположим теперь, что надо составит карту Карно для логического выражения (рис.34). Разместим логические единицы во всех квадратах, которым соответствуют произведения в исходном выражении.

A+B=Q

Рис.34. Заполнение карты Карно и упрощение логического выражения

Далее объединим соседние единицы в один контур группами по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Каждый контур представляет собой новый член упрощенного логического выражения. В карте Карно на рис.34 получилось два контура. Это означает, что новое упрощенное выражение будет состоять из двух членов, связанных функцией ИЛИ.

Рассмотрим нижний контур и заметим, что переменная А встречается в комбинации с В и . В соответствии с правилами алгебры логики В и дополняют друг друга и их можно опустить. Тогда в нижнем контуре остается один член А. Аналогично этому расположенный вертикально контур содержит А и , которые можно опустить, оставив только В. Оставшиеся в результате А и В затем объединяются функцией ИЛИ, что приводит к упрощенному логическому выражению А+В=Q.

Последовательность операций при упрощении логических выражений с помощью карт Карно:

1. Получение логического выражения в ДНФ, как правило, из таблицы истинности.

2. По полученному логическому выражению заносятся единицы в соответствующие клетки карты Карно.

3. Эти единицы в карте Карно объединяются в контуры, охватывающие 2, 4, 8 и т. д. соседних единиц.

4. Проводится упрощение путем исключения членов в контуре, дополняющих друг друга.

5. Полученные таким образом в каждом контуре выражения объединяются логической функцией «ИЛИ».

Рассмотрим карту Карно для трех переменных. Для этого зададимся исходным логическим выражением

Карта Карно для случая трех переменных показана на рис.35. В этой карте имеется восемь (2³) возможных комбинаций переменных А, В и С, которые представлены восемью квадратами на карте. В них занесены четыре единицы, отображающие каждый из четырех членов исходного выражения. Нижний контур содержит В и , поэтому их можно опустить. После этого в составе нижнего контура сохраняются лишь А и , которые в упрощенном выражении дают член . В верхний контур входят С и , поэтому они опускаются как дополняющие друг друга. В результате в этом контуре остается . Окончательно упрощенное логическое выражение имеет вид . Очевидно, что полученное упрощенное логическое выражение потребует для своей схемной реализации значительно меньшее количество логических элементов.

Рис.35. Упрощение логических выражений для трех переменных с помощью карты Карно

Таблица истинности для четырех переменных включает 16 возможных комбинаций. Поэтому карта Карно с четырьмя переменными допускает 16 возможных комбинаций A, B, C и D (рис.36).

Рассмотрим логическое выражение

Занесем в карту Карно (рис.36) шесть единиц, соответствующих значениям термов в исходном выражении.

Рис.36. Упрощение логических выражений для четырех переменных с помощью карты Карно

В полученной карте Карно группы из двух и четырех единиц объединены контурами. Нижний контур из двух единиц дает возможность опустить и . Затем в этом контуре остается член 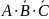. В верхнем конуре из четырех единиц попарно опускаются и , и , так что в результате этого верхний контур дает член . Окончательно полученные в каждом контуре члены объединяются функцией ИЛИ, что дает упрощенное логическое выражение .

Отметим, что для упрощения логических выражений с двумя, тремя и четырьмя переменными применяются общая процедура и одинаковые правила. Чем больше размеры объединяющих контуров, тем больше переменных можно опустить. К недостатку этого метода упрощения логических выражений можно отнести то, что построение карт Карно больших размерностей невозможно в простом виде на плоскости. Однако в настоящее время имеется много компьютерных программ, с помощью которых можно упрощать выражения с количеством переменных более четырех. Кроме того, в качестве исходного выражения не обязательно иметь его в дизъюнктивной нормальной форме.