2 Пример выполнения работы

Синтез модальных регуляторов пониженного порядка.

Дан объект управления

, где . (12)

Требования к качеству управления задаются областью S:

, (13)

где

, .

Необходимо синтезировать модальные регуляторы полного и сокращенного порядков, по возможности обеспечивающие заданные требования к качеству управления.

Решение.

1. Синтез модального регулятора полного порядка. Для расчета модального регулятора полного порядка объект управления (12) представим в операторном виде:

, (14)

где

, .

Регулятор полного порядка ищется на классе звеньев 2-го порядка:

.

Расчетный эталон во всех трех случаях будем назначать по биномиальной схеме с быстродействием ; при этом в случае полного порядка эталон принимает вид

.

Расчет матриц C, X и d осуществляется по методике, изложенной в предыдущей лабораторной работе (см. формулы (9)-(11); подставляя в них коэффициенты объекта и эталона), получаем:

, , .

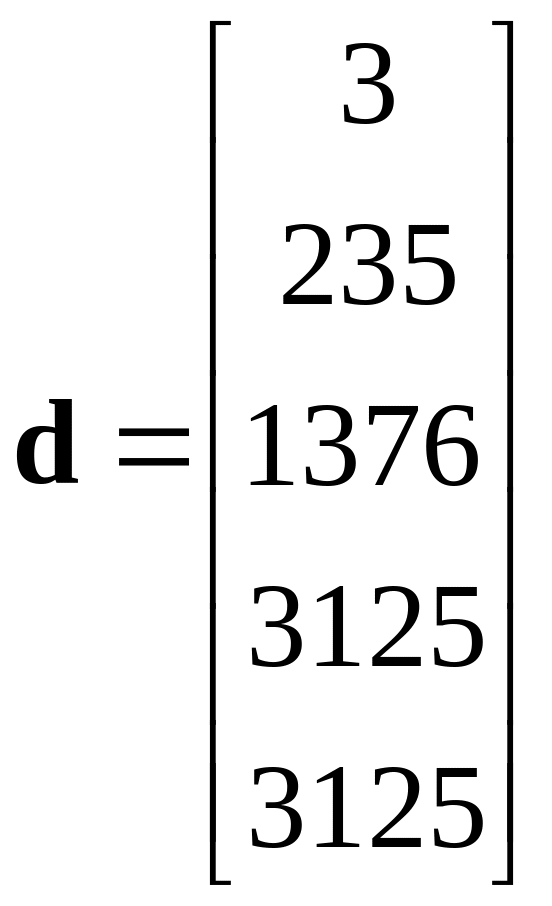Вектор коэффициентов регулятора находится из матричного уравнения

,

решая которое получаем

.

2. Синтез по «доминирующей динамике». Необходимо отметить, что множители и в операторной передаточной функции обладают следующими свойствами:

1) их корни находятся внутри заданной области S;

2) их корни расположены близко друг от друга (по отношению к другим корням в и к границе области S).

Следовательно, в первом приближении данные множители можно сократить, тем самым понизив порядок объекта с третьего до второго. В результате исходный объект управления (12) представляется в следующем виде:

где

, ,

операторы «доминирующей динамики», а

, ,

операторы «структурных возмущений». «Сокращенная» модель объекта управления имеет второй порядок, при этом модальный регулятор для данной системы ищется в виде звена первого порядка:

. (15)

Вектор коэффициентов

модального регулятора (15) находится аналогично модальному регулятору полного порядка, поэтому, опуская все расчеты, приведем только окончательный результат:

.

3. Синтез по «среднеквадратичному отклонению». Для объекта управления (12) регулятор пониженного порядка ищется в виде звена первого порядка (15). В результате расчетный эталон будет иметь четвертый порядок:

.

Матрицы C, X и b (определяемые формулами (9), (10) в предыдущей лабораторной работе, и формулой (9) в текущей) равны

, , .

Матрицу , определяющую метрику в пространстве коэффициентов характеристического полинома замкнутой системы, назначим в виде . Матрица

существует, при этом искомый вектор настроек регулятора X может быть найден из выражения (10); подставляя в (10) матрицы C, Q и b, окончательно получаем

.

Переходные процессы в замкнутых системах для всех трех случаев показаны на рис. 2 (графики 1, 2 и 3 соответственно).

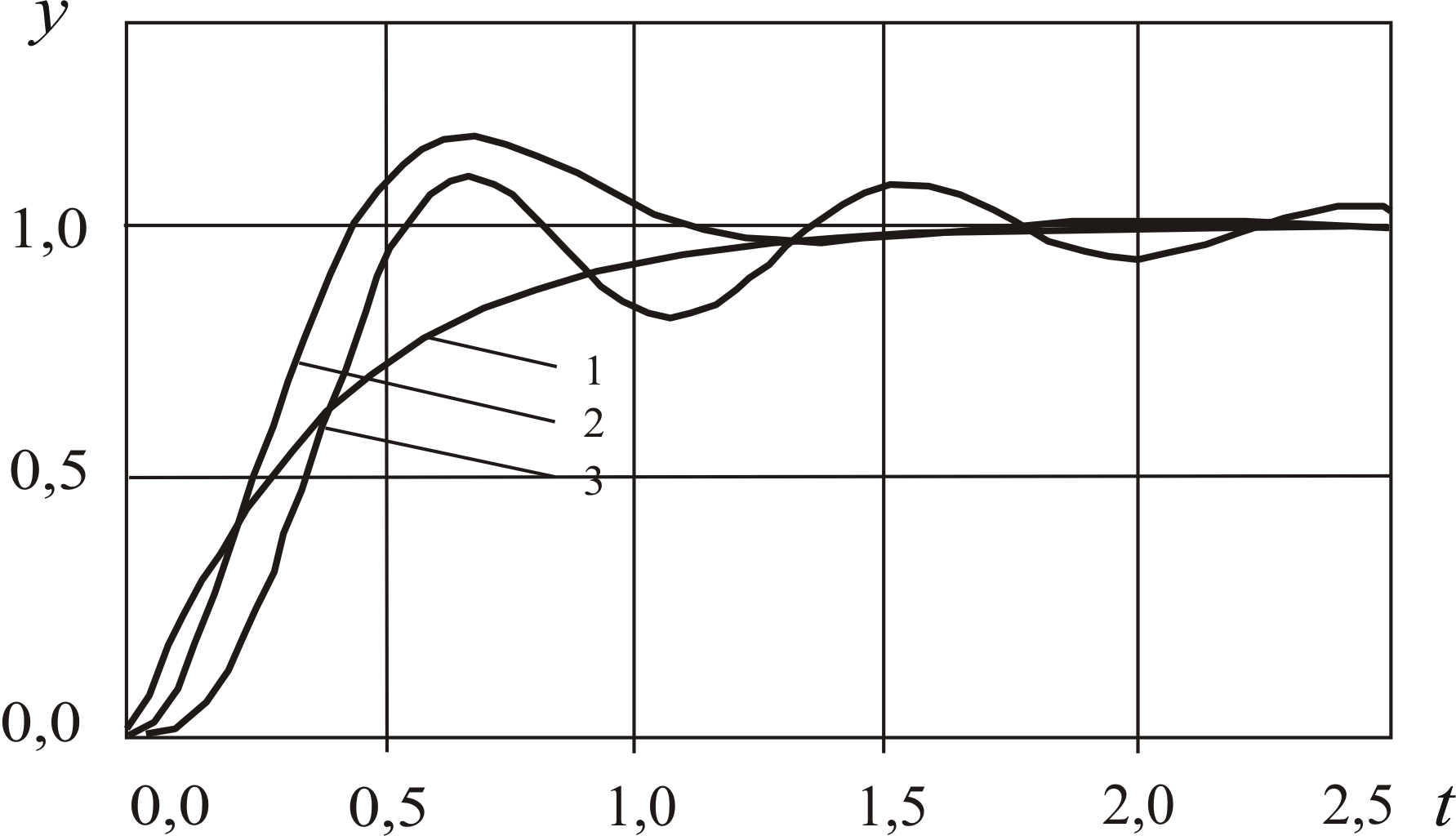
Рис. 2. Переходные процессы в замкнутой системе

Первому графику соответствует и ; второму – и ; третьему – и . Сравнивая полученные показатели качества с заданными (13):

, %,

можем сделать вывод, что переходные процессы 1 и 2 удовлетворяют требуемым показателям качества.