Министерство ПО ОБРАЗОВАНИЮ и науке РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ кибернетики, информатики и связи

Кафедра Кибернетических систем

Методические указания

к лабораторной работе №8

«Методы понижения порядка модального регулятора»

по дисциплине «Теория автоматического управления»

для студентов специальности УИТС и направления УИТСб.

Тюмень

2011

Цель работы: изучить методы понижения порядка модального регулятора; для заданной передаточной функции рассчитать модальные регуляторы пониженного порядка.

1 Необходимые теоретические сведения

1.1 Постановка задачи понижения порядка модального регулятора

В дальнейшем изложении принимаем, что цель управления задается односвязной симметричной областью S, определяющей расположение корней характеристического полинома замкнутой системы. При этом целевое условие записывается в следующем виде: ¹⁾

. (1)

Здесь за обозначено множество корней характеристического полинома замкнутой системы (за обозначена внутренняя часть области ). В классической теории автоматического управления область S чаще всего назначается в виде (см. рис. 1):

,

где - заданное быстродействие системы, а - колебательность. Связь корневых показателей качества управления и с прямыми показателями - временем переходного процесса и быстродействием – устанавливается формулами: ²⁾

, .

На методику синтеза модального регулятора, изложенную в предыдущей лабораторной работе будем ссылаться следующим образом: ³⁾

,

здесь подразумевается, что корни эталонного полинома выбираются по одной из предложенных ранее схем (либо произвольно) в пределах заданной области S. При этом порядок l регулятора может быть произвольным.

____________

¹⁾ подразумевается, что область S расположена в левой части комплексной плоскости С¹;

²⁾ приведенные выражения выведены для систем 2-го порядка; в случае систем более высокого порядка данные формулы могут давать весьма неточные оценки.

³⁾ здесь следует отметить, что в данном разделе нас будет интересовать только задача обеспечения предписанных динамических свойств замкнутой системы, при этом для сокращения объема изложения задачей обеспечения заданного коэффициента усиления мы пренебрегаем как менее содержательной (и несложной в вычислительном отношении)

Свободой в назначении корней эталона (ограниченной областью S) можно воспользоваться по-разному. В данном разделе имеющейся свободой предлагается воспользоваться для понижения порядка модального регулятора. В основу приводимых ниже методов положены следующие рассуждения.

В практических расчетах требование полного порядка зачастую излишне – будем говорить о трех ситуациях:

1) корни характеристического полинома объекта уже лежат внутри заданной области S. В этом случае регулятор, очевидно, вырождается просто в коэффициент усиления, и таким образом, задачи расчета (динамического) регулятора по существу нет;

2) следующий (крайний) случай: все корни характеристического полинома объекта лежат вне заданной области S; в этом случае следует регулировать все корни характеристического полинома объекта, что, очевидно, можно сделать только регулятором полного порядка;

3) на практике чаще встречается следующая (промежуточная) ситуация, когда часть корней характеристического полинома объекта лежит внутри области S (нередко с достаточно большими запасами по быстродействию и колебательности), а другая часть – вне её. При этом естественным представляется по возможности оставить неизменной ту часть системы, которая «удовлетворительна» и регулировать лишь «неудовлетворительную». Понятно, что чем меньше «неудовлетворительных» корней объекта, тем меньшим должен быть и порядок регулятора.

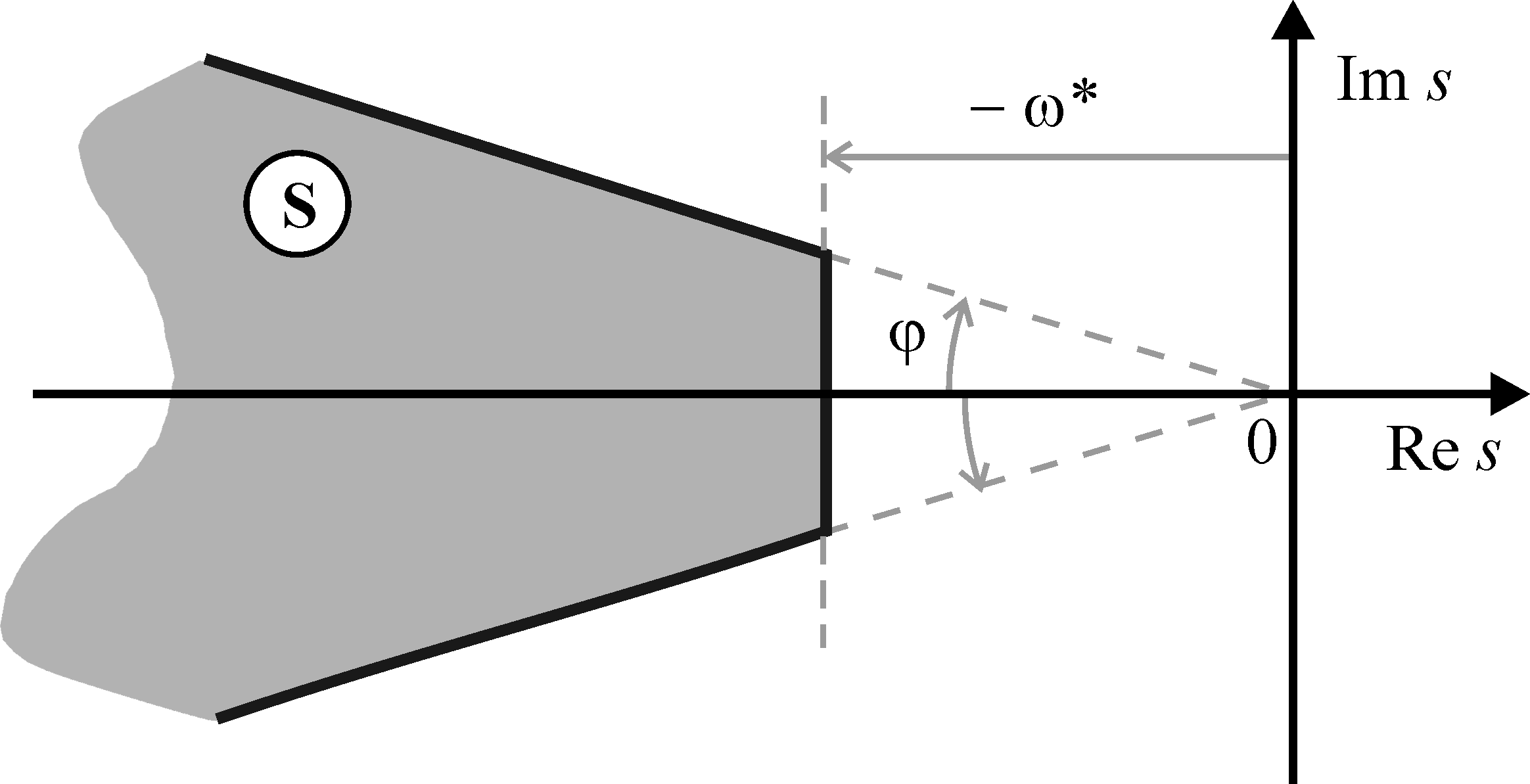
Рис. 1. Область S желаемого расположения корней характеристического полинома (здесь )

В литературе первая часть корней объекта получила название «хорошей динамики» или «структурных возмущений», а вторая – «плохой», или «доминирующей динамики». Название «структурные возмущения» подчеркивает тот факт, что соответствующая часть динамики объекта в расчетах регулятора не участвует. Приводимые ниже методы представляют собой различные схемы синтеза модального регулятора пониженного порядка, основанные на изложенных теоретических посылках.