1.4.2. Многофакторный корреляционный анализ

Методика проведения многофакторного корреляционного анализа основывается на тех же принципах, которые характерны для однофакторного корреляционного анализа. Вместе с тем необходимо тщательно отобрать для анализа наиболее важные и существенные показатели, предварительно исчислив по каждому признаку показатели вариации.

С целью установления существенности влияния факторных признаков на результативный следует исчислить и проанализировать коэффициент регрессии, парные коэффициенты корреляции и критерии их достоверности. Далее необходимо составить уравнение множественной регрессии, предварительно установив тип функции.

Уравнение множественной линейной регрессии с тремя переменными имеет следующий вид:

y = a₀ + a₁ x₁ + a₂ x₂

y = –20,8 + 1,69x₁ – 0,872

Для определения параметров уравнения может быть применена следующая система нормальных уравнений:

Для решения системы нормальных уравнений по исходным данным необходимо вычислить , , , , .

Результаты расчетов занести в таблицу 8.

Таблица 8 – Расчет показателей для определения параметров уравнения множественной регрессии

Предприятия	Заработная плата	Норма выработки	ПТ	Расчет показателей для определения параметров уравнения множественной регрессии
	y	x1	x2	yx2	x1x2
1	2	3	4	5	6	7	8

Продолжение табл. 8

1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	325 280 190 285 183 125 113 118 253 189 195 178 115 197 191 127 185 280 216 191	200 180 140 191 125 97 86 82 170 135 137 126 89 150 128 108 133 190 151 147	14 15 18 16 14 17 29 19 20 18 21 23 20 18 22 24 19 26 27 21	4550 4200 3420 4560 2562 2125 3277 2249 5060 3402 4095 4094 2300 3546 4202 3048 3515 7280 5832 4011	2800 2700 2520 3056 1750 1649 2491 1559 3400 2430 2870 2898 1780 2700 2816 2592 2527 4940 4077 3089	40000 32400 19600 36481 15625 9409 7396 6724 28900 18225 18769 15876 7921 22500 16384 11664 17689 36100 22801 21609	196 225 324 256 196 289 841 361 400 324 441 529 400 324 484 576 361 676 729 441
Итого	3936	2765	401	77321	54644	406073	8373

Решение системы нормальных уравнений:

Уравнение множественной регрессии имеет следующий вид:

– 20,8 + 1,69x₁ – 0,8x₂

Коэффициент множественной корреляции для двухфакторной линейной модели исчислить по формуле:

;

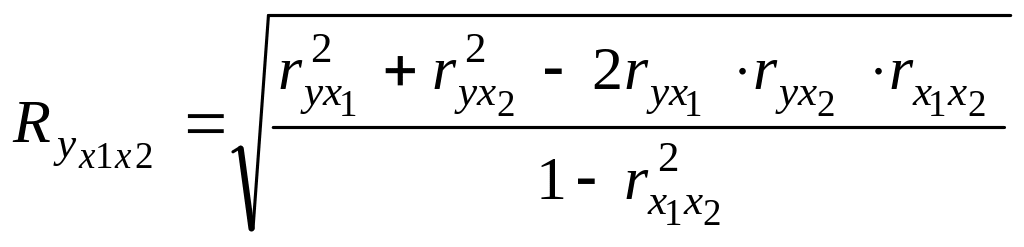r_yx1 = 0,98; r_yx2 = – 0,038; r_x1x2 = – 0,28; R_yx1x2 = 0,9037.

Статистическую оценку параметров уравнения множественной регрессии на их значимость оценить t – критерием Стьюдента:

;

,

где k – число факторов уравнения регрессии.

8,6949

– 0,3355

Достоверность коэффициента множественной корреляции определить по формуле:

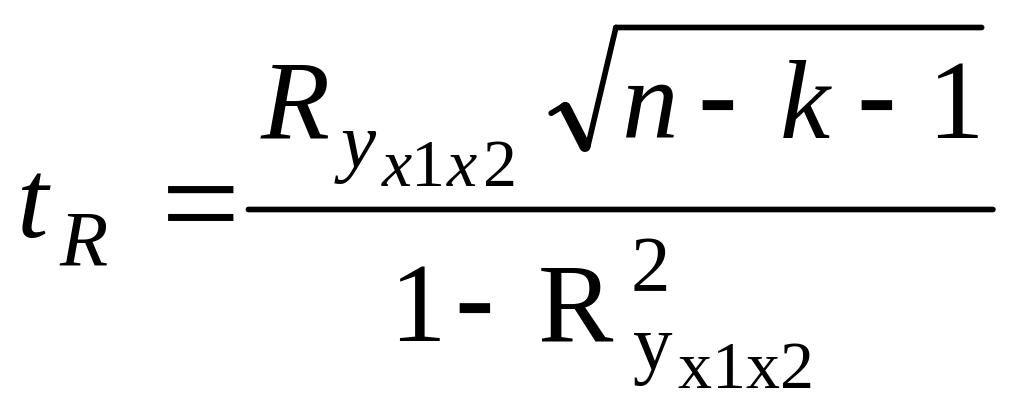
t_R = 19,722

Фактическое значение (t_факт) критерия сопоставить с табличным (t_табл) при заданном уровне вероятности и числе степеней свободы и сделать краткие выводы.

При числе степеней свободы: f = k – (p+1)

f = 20 – (3 +1) = 18

при значимости 0,18 t_табл = 2,8784