1.4. Корреляционно-регрессионный анализ (однофакторный, многофакторный)
1.4.1. Однофакторный корреляционный анализ
1. Учитывая расположение точек на поле корреляции, ориентировочно определить характер зависимости между признаками и соответствующее ей математическое уравнение, которое может быть описано одной из функций следующего вида:
– прямая линия:
,
– гипербола:
,
– парабола второго
порядка:
,
– степенная
функция:
.
и т.д.
2. Составить систему нормальных уравнений для выбранной функции.
Например, уравнению прямой линии соответствует следующая система нормальных уравнений:
Для определения параметров а и b по исходным данным необходимо вычислить
,
,
,
.
a = – 40
b = 1,74
Таблица 5 – Расчет показателей для определения параметров уравнения.
Предприятия |
x |
y |
хy |
x2 |
1 |
200 |
325 |
65000 |
40000 |
2 |
180 |
280 |
50400 |
32400 |
3 |
140 |
190 |
26600 |
19600 |
4 |
191 |
285 |
54435 |
36484 |
5 |
125 |
183 |
22875 |
15625 |
6 |
97 |
128 |
12125 |
9409 |
7 |
86 |
113 |
9718 |
7396 |
8 |
82 |
118 |
9676 |
6724 |
9 |
170 |
283 |
43010 |
28900 |
10 |
135 |
189 |
28515 |
18225 |
11 |
137 |
195 |
26715 |
18769 |
12 |
126 |
178 |
22428 |
15876 |
13 |
89 |
115 |
10235 |
7921 |
14 |
150 |
197 |
29550 |
22500 |
15 |
128 |
191 |
24448 |
16384 |
16 |
108 |
127 |
13716 |
11664 |
17 |
133 |
185 |
24605 |
17689 |
18 |
190 |
280 |
53200 |
36100 |
19 |
151 |
216 |
32616 |
22801 |
20 |
147 |
191 |
28077 |
21609 |
Итого: |
2765 |
3936 |
584944 |
406073 |
Степень тесноты связи между признаками можно определить при помощи коэффициента корреляции:
– для малых выборок по формуле:
,
где r – коэффициент корреляции;
x, y – значения изучаемых признаков;
– средние значения признаков.
– для больших
выборок по формуле:
где 
– среднее значение изучаемых признаков;
– среднее квадратическое отклонение
признаков.
Расчеты, необходимые для вычисления коэффициента корреляции, должны быть занесены в таблицу 6.
138,25
196,8
29247,2
34,5
60,2
r =0,98
Таблица 6 – Расчет показателей для исчисления коэффициента корреляции.
№ п/п предприятия |
Выполненная норма выработки, % |
Заработная плата, тыс.руб |
Xy |
Отклонения |
|||
линейные |
квадратичные |
||||||
|
x |
y |
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
200 180 140 191 125 97 86 82 170 135 137 126 89 150 128 108 133 190 151 147 |
325 280 190 285 183 125 113 118 253 189 195 178 115 197 191 127 185 280 216 191 |
65000 50400 26600 54435 22875 12125 9718 9676 43010 25515 26715 22428 10235 29550 24448 13716 24605 53200 32616 28077 |
62 42 2 53 – 13 – 41 – 52 – 56 32 – 3 – 1 – 12 – 49 2 – 10 – 30 – 5 52 13 9 |
128 83 – 7 88 – 14 – 72 – 84 – 79 56 – 8 – 2 – 19 – 82 0 – 6 – 70 – 12 83 19 –6 |
3844 1764 4 2809 169 1681 2704 3136 1024 9 1 144 2401 144 100 900 25 2704 169 91 |
16384 6889 49 7744 196 5184 7056 6241 3136 64 4 361 6724 0 36 4900 144 6889 361 36 |
Сумма |
Σx = 2765 |
Σy =3936 |
Σxy = 584944 |
–5 |
–4 |
Σ |
Σ = 72398 |
=
23813
4. Оценку достоверности коэффициента регрессии b уравнения yx = a + bx рассчитать по формуле:
,
где tфакт – фактическое значение критерия достоверности;
b – коэффициент регрессии;
Sb – средняя ошибка коэффициента регрессии.
,
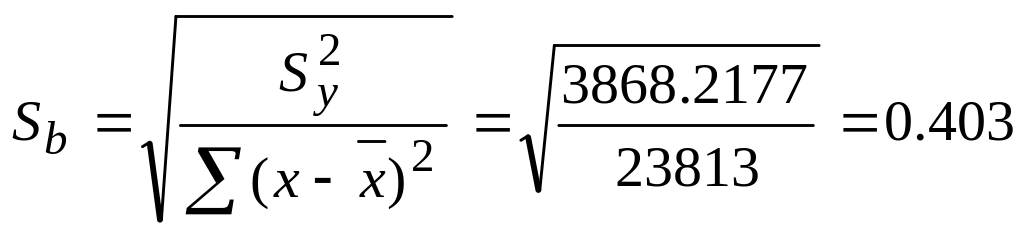где
– средний квадрат отклонений фактических
значений y от
теоретических, т.е. вычисленных по
уравнению
.
,
где n – число единиц совокупности.
Расчеты для определения Sb провести в таблице 7.
Таблица 7 – Расчет показателей для определения Sb
№ п/п |
y |
x |
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
325 280 190 285 183 125 113 118 253 189 195 178 115 197 191 127 185 280 216 191 |
200 180 140 191 125 97 86 82 170 135 137 126 89 150 128 108 133 190 151 147 |
302 267,8 199,4 286,61 173,75 125,87 107,06 100,22 250,7 190,85 194,27 175,46 112,19 216,5 178,88 144,68 187,43 284,9 218,21 211,37 |
105,6 71,4 3 90,21 – 22,65 – 70,53 – 89,34 – 96,18 54,3 – 5,55 – 2,13 – 20,94 – 84,21 20,1 – 17,52 – 51,72 – 8,97 88,5 21,81 14,97 |
11151,36 5097,96 9 8137,84 513,02 4974,5 7981,63 9250,59 2948,49 30,80 4,53 438,48 7091,32 404,01 306,95 2674,96 80,46 7832,25 475,67 224,1 |
Сумма |
Σy = 3936 |
Σx = 2765 |
Σxy = = 3928,15 |
0 |
Σ = = 69627,92 |
3868,2177
0,1624
0,403
По таблице t – Стьюдента установить значение tтабл при достоверном уровне вероятности и сравнить с tфакт:
Оценку достоверности коэффициента линейной корреляции исчислить по формуле:
,
где Sr – стандартная ошибка коэффициента линейной корреляции.
Зная стандартную ошибку Sr, определить фактический критерий достоверности (нормированное отклонение tфакт).
tфакт = 108,9
По таблице t–Стьюдента установить значение tтабл при установленном уровне вероятности и числе степеней свободы, равном n –1.