11

Лабораторная работа 13а Теплопроводность твердых тел

Цель работы: экспериментально исследовать явление теплопроводности твердых тел.

Общее уравнение переноса. При нарушениях равновесия в средах возникают потоки тепла, либо массы, либо импульса и т.п. В связи с этим, соответствующие процессы носят название явлений переноса. Явления переноса представляют собой необратимые процессы.

Введем некоторую скалярную величину , которая характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация, электрический заряд и т.д.

Известно, что градиентом какой-либо величины (скалярной) , зависящей от координат, называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания и численно равен быстроте этого возрастания.

Если в равновесном состоянии величина постоянна по объему, то при наличии градиента , имеет место движение этой величины в направлении его уменьшения.

Для удобства расчетов предположим, что в неограниченной среде перенос количества происходит в одном направлении, вдоль которого направим ось . То есть, пусть ось направлена вдоль градиента . Выделим в среде площадку , перпендикулярную к оси (рис.1).

Рис.1. К выводу общего уравнения переноса

Площадку пересекают молекулы, пришедшие со всевозможных направлений и пересекающие ее в направлении отрицательных значений оси . Число молекул в объеме равно , где – концентрация молекул вещества. Частица движется со средней скоростью и, следовательно, проходит среднюю длину свободного пробега за время . Поэтому средняя частота столкновений (среднее число столкновений за одну секунду) равна . В течение времени число молекул из данного объема в результате столкновений летят изотропно по всевозможным направлениям, в том числе и в направлении площадки , которая видна из элемента объема под углом . Число молекул, пересекших площадку и на пути от элемента объема не испытавших ни одного последующего столкновения, равно

, (1)

где – множитель, который учитывает выбывание молекул из пучка из-за столкновений с другими молекулами;

– множитель, который определяет число молекул, приходящихся на данный телесный угол;

– расстояние от объема до центра площадки .

Поток числа молекул, пересекающих поверхность в единицу времени, равен

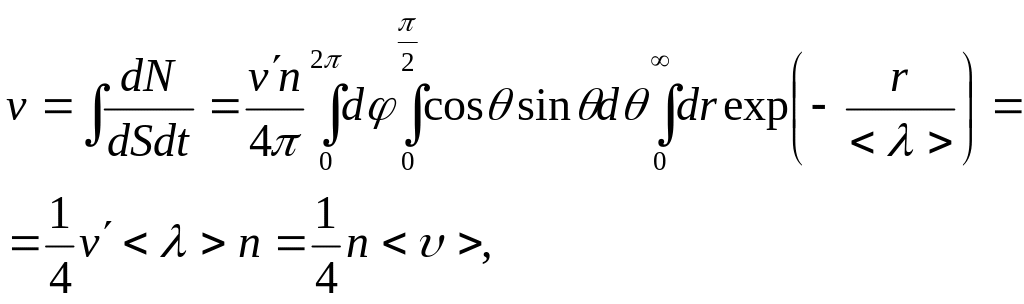(2)

где – концентрация молекул вещества,

– средняя скорость молекул вещества,

– среднее число столкновений в секунду,

– средняя длина свободного пробега.

Теперь вычислим среднее расстояние вдоль оси , которое проходят молекулы, пересекающие площадку после последнего столкновения. Из теории вероятности известно, что среднее значение непрерывно изменяющейся величины равно

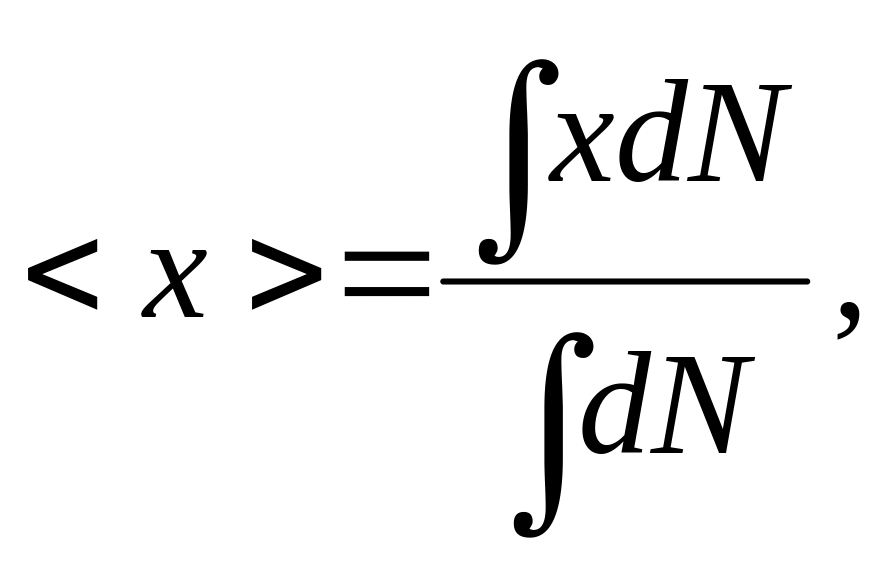(3)

где дается формулой (1). В результате интегрирования (3) выражение для среднего расстояния, пробегаемого молекулами, пересекающими площадку (рис.1) после последнего столкновения примет вид

, (4)

где – средняя длина свободного пробега молекулы.

Запишем на расстоянии от площадки с учетом того, что эта величина в большинстве случаев достаточно мала и ограничившись первым членом разложения в ряд Тейлора в точке :

. (5)

Поток числа молекул в направлении оси , согласно формуле (2) равен . Следовательно, поток сквозь площадку в направлении отрицательных значений оси равен

, (6)

а в направлении положительных значений оси дается выражением

, (7)

Следовательно, суммарный поток в положительном направлении оси в точке имеет вид

, (8)

где – концентрация молекул вещества,

– средняя скорость молекул вещества,

– средняя длина свободного пробега молекулы,

– частная производная величины по .

Уравнение (8) является основным уравнением процессов переноса количества .

Здесь использован символ частной производной, поскольку величина зависит и от времени и от координаты .

Уравнение Фурье для теплопроводности твердых тел. Коэффициент теплопроводности твердых тел. Теплопроводность – это процесс переноса теплоты из области с более высокой температурой в область, где она ниже, в результате теплового движения микрочастиц в среде. Таким образом, передача теплоты при теплопроводности приводит к выравниванию температуры среды.

Механизм переноса тепла в твердом теле отличается от данного механизма в газах и жидкостях. Он определяется характером тепловых движений в твердом теле, то есть спецификой строения твердого тела. Твердое тело представляет собой совокупность частиц, находящихся в состояниях устойчивого равновесия и совершающих колебания каждая около своего такого положения устойчивого равновесия. Эти колебания независимы друг от друга и могут передаваться (со скоростью звука) от одних частиц к другим. При этом образуется волна, которая и переносит энергию колебаний. Следовательно, теплопроводность в твердом теле осуществляется не за счет перемещения молекул или атомов, а посредством взаимодействия между частицами, в результате которого их тепловое движение приобретает коллективный характер. Квантовая теория позволяет сопоставить распространяющимся в твердом теле со скоростью звука колебаниям газ квазичастиц – фононов, представляющих собой кванты коллективных колебательных движений. Таким образом тепловое движение в твердом теле описывается с помощью модели идеального газа фононов.

Таким образом, введение фононов позволяет рассматривать твердое тело как объем, заполненный газом невзаимодействующих квазичастиц-фононов. Фононы, подобно атомам идеального газа, сталкиваясь друг с другом, движутся между стенками сосуда – поверхностями, ограничивающими твердое тело. Фононы не являются частицами: их нельзя представить в вакууме, их число может изменяться при нагревании или охлаждении твердого тела, т.е. число фононов не сохраняется. Фононы могут существовать в любом из состояний с уровнем энергии , где – частота колебаний атомов.

Рассмотрим передачу теплоты в твердом теле, которая осуществляется исключительно путем теплообмена (так как в твердом теле не может возникать конвекция, т.е. перемещение массы вещества вместе с теплом). Будем предполагать, что объем системы остается постоянным, так что никаких перемещений вещества в процессе передачи теплоты не возникает. При этом, ограничимся рассмотрением одномерной задачи, когда температура среды, помимо времени, зависит только от одной пространственной координаты.

Как было сказано ранее, фононы в твердом теле подобны атомам идеального газа, и поэтому сначала рассмотрим уравнение переноса для идеального газа (8).

В этом случае (в случае теплопроводности) есть средняя энергия теплового движения, приходящаяся на одну молекулу. Она переменна в том случае, если от точки к точке меняется температура. При этом – поток теплоты, который входил в уравнение (8) и который далее будем обозначать .

Из теоремы о равнораспределении энергии по степени свободы имеем

(9)

где – температура,

– число степеней свободы,

– постоянная Больцмана,

– число Авогадро,

– универсальная газовая постоянная,

– молярная теплоемкость газа при постоянном объеме.

Тогда подставляя это в уравнение переноса (8) получим

, (10)

где – плотность вещества,

– удельная теплоемкость газа при постоянном объеме,

– масса молекулы.

То есть уравнение Фурье для теплопроводности

, (11)

где – плотность теплового потока (то есть количество теплоты, проходящее в единицу времени через единицу площади поверхности);

– коэффициент теплопроводности;

– частная производная температуры по .

Уравнение (11) можно обобщить на трехмерный случай:

, (12)

или в векторном виде:

, (13)

где – вектор плотности теплового потока;

– коэффициент теплопроводности;

– градиент температуры.

В уравнении Фурье для теплопроводности знак “–“ выражает направление переноса тепла от области с большей температурой к области с меньшей температурой, тогда как градиент направлен в сторону возрастания этой величины.

Коэффициент пропорциональности в уравнении Фурье для теплопроводности (13) – это коэффициент теплопроводности. Он является физическим параметром, характеризующим интенсивность процесса теплопроводности в веществе, т.е. скорость переноса тепла.

В соответствии с уравнением (10), учитывая, что по аналогии с движением молекул идеального газа в твердом теле рассматривается движение фононов, получаем, что коэффициент теплопроводности твердых тел равен

, (14)

где – плотность твердого тела,

– скорость звука в твердом теле,

– средняя длина свободного пробега фононов,

– удельная теплоемкость твердого тела.

Физический смысл коэффициента теплопроводности вытекает непосредственно из закона Фурье (13): коэффициент теплопроводности численно равен плотности теплового потока при градиенте температуры, равном единице. Это означает, что в случае однородного изотропного тела коэффициент теплопроводности численно равен количеству теплоты, проходящему через единицу поверхности в единицу времени вследствие теплопроводности при перепаде температуры на единицу длины нормали, равном одному градусу.

Размерность коэффициента теплопроводности в системе СИ – ватт на метр-кельвин: .

Теплопроводность зависит от агрегатного состояния вещества, его состава, чистоты, температуры, давления и других факторов.

Что касается зависимости от агрегатного состояния, то теплопроводность твердых тел при нормальных условиях обычно в несколько тысяч раз больше теплопроводности жидкостей, и в сотни тысяч и миллионы раз больше, чем теплопроводность газов. Также следует отметить, что теплопроводность аморфных тел значительно меньше, чем теплопроводность кристаллов. Поликристаллические тела обладают промежуточной теплопроводностью между теплопроводностями монокристаллов и аморфных тел. Численное значение для стали (в зависимости от марки) при нормальных условиях лежит в интервале .

Кроме того, следует отметить, что в твердых телах тепло переносится не только тепловыми колебаниями атомов и молекул (фононами), как говорилось выше, но и свободными электронами твердого тела. Электроны активно участвуют в переносе тепла. Для описания электронной теплопроводности на основе электронной кинетической теории вводится понятие о средней длине свободного пробега электронов по аналогии с длиной свободного пробега молекул газа. В этом случае коэффициент теплопроводности твердого тела вычисляется по формуле, аналогичной (14):

, (15)

где – средняя скорость свободных электронов в твердом теле,

– средняя длина свободного пробега свободных электронов,

– плотность электронного «газа»,

– удельная теплоемкость электронного «газа»,

Таким образом, теплопроводность твердых тел в подавляющем большинстве случаев обусловлена двумя механизмами: движением электронов проводимости (электронная теплопроводность, æ_эл) и тепловыми колебаниями атомов и молекул твердого тела (фононная теплопроводность, æ_ф). Первый механизм доминирует в металлах, второй определяет теплопроводность неметаллов. В некоторых полупроводниках, полуметаллах и сильно разупорядоченных сплавах оба механизма дают сравнимые вклады в теплопроводность.

Из выше сказанного следует, что суммарная теплопроводность твердого тела определяется формулой

, (16)

где – электронная теплопроводность,

– фононная теплопроводность.

Для металлов и сплавов теплопроводность можно оценить, используя закон Видемана – Франца:

, (17)

где – число Лоренца,

– электропроводность, ,

– температура, К.

Подобное соотношение было впервые установлено учеными Видеманом и Францем и поэтому носит их имя. Важность формулы (17) в том, что она показывает связь теплопроводности с электропроводностью.

Для большинства металлов и сплавов закон Видемана – Франца справедлив при высоких и близких к абсолютному нулю температурах. Для чистых металлов в области промежуточных тимператур этот закон дает завышенные значения æ. Для сплавов он дает заниженные значения теплопроводности (до 10 раз при температурах около 20К для сильно разупорядоченных многокомпонентных сплавов).