Свойства кольца.

1) Умножение дистрибутивно относительно вычитания, т.е.

.

Доказательство.

.

2) .

Доказательство. Т.к. . Аналогично доказывается, что .

Утверждение, обратное свойству 2), неверно. А именно, существуют кольца, в которых произведение двух ненулевых элементов равно нулю, т.е но . Такие кольца называются кольцами с делителями нуля. Например, множество непрерывных функций – кольцо с делителями нуля. Действительно, если ,

Аналогично, − множество матриц размера − кольцо с делителями нуля.

3) Если − отличный от нуля элемент из , не являющийся делителем нуля, и

(закон сокращения в кольце). Аналогично,

Доказательство.

4)

Доказательство.

4°.Поле, свойства поля.

Пусть P – множество, содержащие не менее двух элементов.

Определение 10. Множество с заданными на нём алгебраическими операциями сложения + и умножения называется полем и обозначается (), если:

1) (P;+) – абелева группа.

2) (P\{0};) – абелева группа.

3) Умножение дистрибутивно относительно сложения, т.е.

Т.о., поле – это коммутативное и ассоциативное кольцо с единицей, в котором все ненулевые элементы составляют мультипликативную группу.

Примеры полей.

1. − примеры полей.

2. (,,) − поле.

Свойства поля.

1) В поле Р нет делителей нуля.

Доказательство. Пусть Умножим на : . С другой стороны,

2) Свойство сокращения на ненулевой элемент: из

3) , уравнение в поле P имеет единственное решение .

Доказательство. При доказываемое свойство – это свойство группы, при − свойство кольца.

Решение уравнения обозначается и называется частным от деления на . Т.о., в поле определено деление на ненулевой элемент.

Вывод. В произвольном поле можно проводить все операции, как в обычной арифметике: сложение, вычитание, умножение, деление на ненулевой элемент, раскрытие скобок, приведение подобных, … .

Итак, алгебраические структуры – это множества с алгебраическими операциями. Дальнейшее обобщение – алгебраические системы, являющиеся совокупностью множества, алгебраических операций и отношений. Это стык алгебры и математической логики.

5°.Подполугруппа, подгруппа.

Пусть − бинарная алгебраическая операция на .

Определение 11. Подмножество называется замкнутым относительно , если выполняется

Если подмножество множества замкнуто относительно , то на определена операция: каждой паре ставится в соответствие

Определение 12. Такая операция на называется операцией, индуцированной операцией .

Лемма 3. Пусть − полугруппа и замкнуто относительно Тогда является полугруппой относительно индуцированной операции.

Доказательство. Для доказательства леммы достаточно показать, что операция ассоциативна на множестве Это очевидно, так как все элементы являются элементами , а на введенная операция ассоциативна.■

Определение 13. Пусть − полугруппа. Подмножество , замкнутое относительно , называется подполугруппой.

Пример. − полугруппа (и даже группа), а − подполугруппа (но не группа).

Определение 14. Пусть пара () – группа. называется подгруппой, если X замкнуто относительно и X − группа относительно индуцированной операции.

Определение 15. Пусть тройка (P,+,) − кольцо (поле). Подмножество называется подкольцом (подполем), если Y замкнуто относительно и и Y является кольцом (полем).

Пример. − подполе в поле

Теорема 5. Пусть () – группа. является подгруппой в

1) X замкнуто относительно ; 2) , где − нейтральный элемент в ;

3) существует .

Доказательство. Достаточность − очевидна.

Необходимость. Пусть − подгруппа в . Тогда условие 1) выполнено по определению подгруппы.

Проверим условие 2). Так как − подгруппа, то − нейтральный элемент в . Докажем, что , т.е. совпадает с нейтральным элементом в . Действительно, умножим равенство на (симметричный элемент к в смысле , т.е. ). С одной стороны имеем: , с другой − . Отсюда следует, что .

Осталось проверить 3). Пусть . Тогда , являющийся симметричным в , т.е. . Это и означает выполнение условия 3).■

Аналогичные теоремы доказываются для подколец и подполей.

Теорема 6. Если в группе взяты две подгруппы и , то их пересечение , т.е. совокупность элементов, лежащих одновременно в обоих множествах, также будет подгруппой группы .

Доказательство. Действительно, если в пересечении содержатся элементы и , то они лежат в подгруппе , а потому в лежат и произведение , и симметричный элемент . По тем же соображениям элементы и принадлежат подгруппе , а потому они входят и в .■

Интересный пример подгруппы − циклические подгруппы. Вначале введем некоторые понятия. Если − элемент группы , то n-ой степенью элемента называется произведение n элементов, равных . Отрицательные степени элемента вводятся как произведения сомножителей, равных . Легко видеть, что . Для доказательства достаточно взять произведение сомножителей, из которых первые равны , а остальные − , и произвести все сокращения. Под нулевой степенью элемента будем понимать нейтральный элемент. В силу обобщенной ассоциативности легко показать, что имеют место равенства:

(3)

Обозначим подмножество группы , состоящее из всех степеней элемента .

Лемма 4. Множество является подгруппой группы .

Доказательство очевидно.

Определение 16. Подгруппа называется циклической подгруппой группы .

Легко видеть, что циклическая подгруппа всегда коммутативна, даже если сама группа некоммутативна. Если все степени элемента являются различными элементами, то называется элементом бесконечного порядка . Если существуют и из , такие, что , то называется элементом конечного порядка. Легко видеть, что в этом случае . Наименьшее такое, что называется порядком элемента .

Определение 17. Группа называется циклической группой, если она состоит из степеней одного из своих элементов , т.е. совпадает с одной из своих циклических подгрупп . Элемент в этом случае называется образующим элементом группы .

Примеры.

1) − циклическая группа с образующим элементом 1.

2) Группа корней n-ой степени из 1 − циклическая мультипликативная группа с образующим элементом, получаемом при .

6°.Гомоморфизм и изоморфизм групп

Определение 18. Пусть и − множества, и − бинарные операции (на и соответственно). Гомоморфизмом из в называется отображение такое, что

Пример. Отображение является гомоморфизмом из в Это следует из справедливости равенства

Замечания.

1. Аналогично определяется понятие гомоморфизма, если на множествах и определены несколько операций.

2. Так как полугруппа, группа, кольцо и т.д. множества с операциями, то ясно, что такое гомоморфизм полугрупп, групп и т.д.

Определение 19. Изоморфизм − это биективный гомоморфизм.

Определение 20. Пара изоморфна паре , если изоморфизм из в .

Обозначение. означает, что изоморфно . Иногда пишут .

Примеры.

1. Отображение является изоморфизмом из в 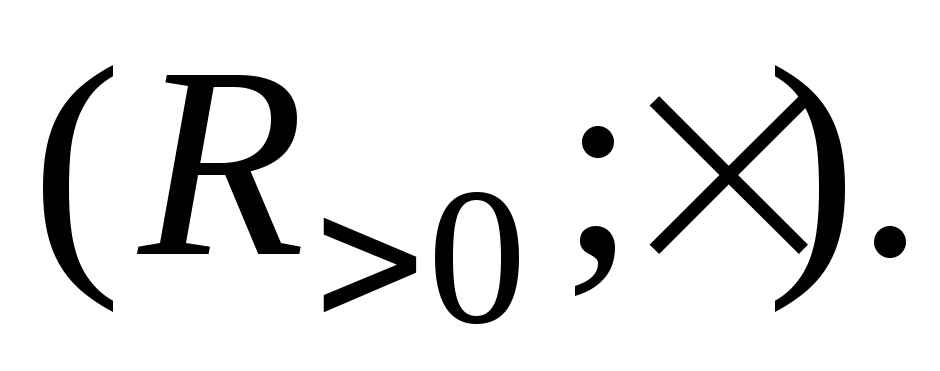Действительно, это отображение является гомоморфизмом (см. предыдущий пример) и биективным отображением (в силу свойств экспоненциальной функции).

2. В начале §1 комплексные числа определялись как пары действительных чисел. Множество пар вида отождествлялись с множеством действительных чисел . Это возможно в силу изоморфизма этих двух множеств.

3. Отображение такое, что является изоморфизмом.

4. Отображение такое, что является изоморфизмом аддитивной группы и не является гомоморфизмом мультипликативной группы. Действительно, , но .

Теорема 7. Пусть − изоморфизм. Тогда

1. если − коммутативна, то − также коммутативна;

2. аналогично для ассоциативности;

3. если − нейтральный элемент в относительно , то − нейтральный элемент в относительно ;

4. если и − взаимно обратные элементы из , то и − взаимно обратные из .

Доказательство.

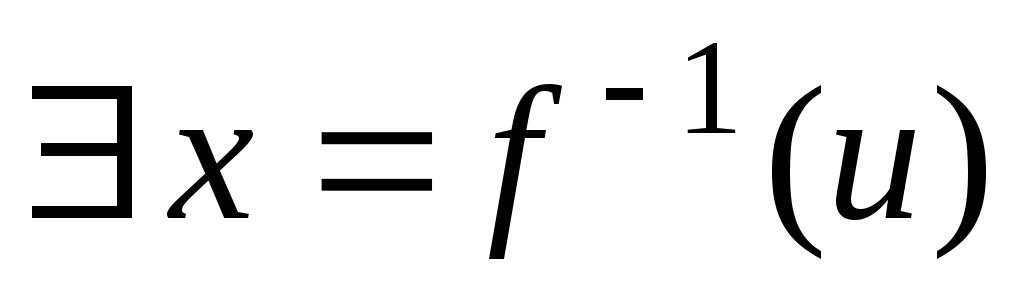1. Пусть и . Докажем, что . Так как и , то последнее равенство можно переписать в равносильном виде , откуда следует . Справедливость последнего равенства следует из коммутативности операции .

2. Доказывается аналогично 1). Пусть . Тогда : , , . Далее по аналогии.

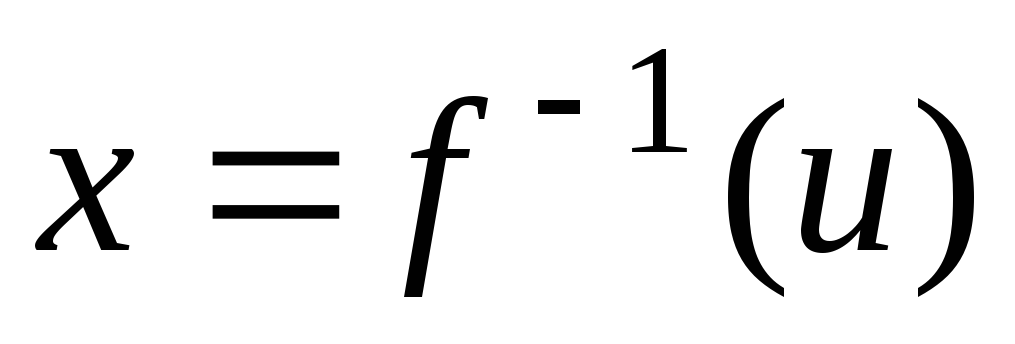3. Пусть . Докажем, что . Пусть . Тогда . Аналогично доказывается .

4. Дано: , где − нейтральный элемент в . Действуя на все элементы этого равенства функцией , получаем требуемое равенство.■

Следствие. Из доказанной теоремы следует, что если и − группа, то − также группа. Аналогично для колец и полей.

Теорема 8. Все бесконечные циклические группы изоморфны между собой. Изоморфны между собой также и все конечные циклические группы данного порядка .

Доказательство. Действительно, любая бесконечная циклическая группа с образующим элементом отображается взаимно однозначно на аддитивную группу , если каждому элементу этой группы ставится в соответствие число . Это отображение является изоморфизмом, так как согласно (3) при перемножении степеней элемента показатели складываются. Если рассматривается конечная циклическая группа порядка с образующим элементом , то, рассматривая мультипликативную группу корней ­−ой степени из единицы и обозначая , изоморфизм строится сопоставлением элементу группы числа . Изоморфность такого отображения следует из следствия к теореме из § 1.■

18