Свойства группы.

1°. В группе G нейтральный элемент и симметричный элемент.

Доказательство следует из теорем 1 и 2.

2°. Для уравнения имеют единственное решение:

, .

Доказательство. Покажем, что – решение уравнения . Имеем: , т.е. − решение.

Если z – другое решение, то после умножения слева на x – единственное решение. Аналогично для другого уравнения.

3°. Закон сокращения в группе. Если .

Доказательство следует из свойства 2°.

Важный пример (группа перестановок степени ).

Пусть ­­− произвольное множество из элементов; например,

Определение 8. Перестановкой степени называется взаимнооднозначное отображение множества в .

Множество всех перестановок степени обозначается . Каждую перестановку будем в дальнейшем обозначать строчной буквой греческого алфавита: Перестановка изображается двурядным символом:

.

Такой символ обозначает отображение

Лемма 1. Число различных перестановок степени равно

Доказательство. В качестве первого элемента можно выбрать любой из элементов, в качестве второго − любой из оставшихся элементов, и т.д. Всего различных возможностей выбора Таким образом, ■

На множестве перестановок вводится операция умножения по формуле

Например, если

то

Лемма 2. Множество образует группу, не являющуюся коммутативной.

Доказательство. Вначале проверим ассоциативность умножения. Пусть и Тогда по определению легко проверить выполнение равенства Тождественная перестановка является нейтральным элементом в рассматриваемом множестве, симметричный элемент получается перестановкой строк. Некоммутативность легко проверяется на предыдущем примере.■

Замечание. Если и − коммутативная операция, то таблица Кэли симметрична относительно диагонали.

3°.Кольцо, свойства кольца.

В алгебре изучаются множества и с несколькими, например, с двумя, алгебраическими операциями.

Определение 9. Непустое множество называется кольцом и обозначается , если выполняются условия:

1) (K;+) – абелева группа.

2) умножение ассоциативно, т.е.

3) умножение дистрибутивно относительно сложения, т.е.

, .

Кольцо называется коммутативным (понятия абелева кольца нет!!!), если умножение коммутативно. Если относительно умножения существует нейтральный элемент, то кольцо называется кольцом с единицей.

Примеры колец.

1. образуют коммутативное кольцо с единицей относительно обычных операций сложения и умножения.

2. Множество {0}, содержащее лишь одно число 0, образует кольцо, называемое нулевым кольцом.

3. Множество 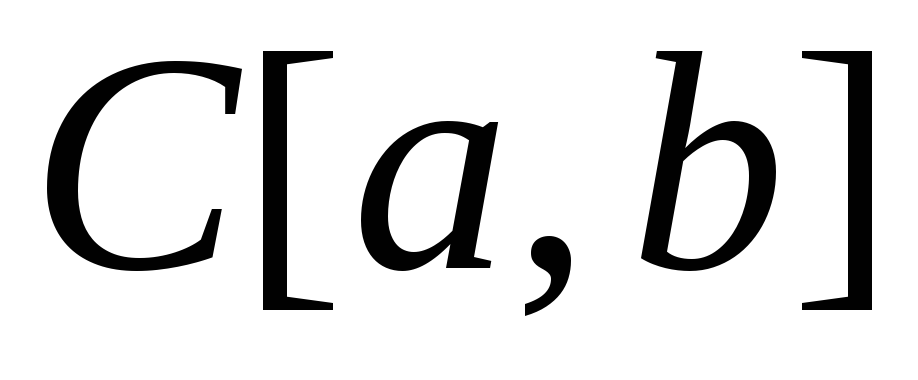непрерывных на отрезке функций с операциями + и , определенными следующим образом:

, ,

образует коммутативное кольцо с единицей.

4. Множество V₃ всех векторов пространства относительно операций сложения векторов и векторного произведения векторов, образует кольцо.

5. Рассмотрим пространство битовых строк (последовательностей длины , состоящих из нулей и единиц), относительно операций (исключающее «или») и (логическое умножение), которые задаются таблицами:

	0	1
0	0	0
1	0	1

	0	1
0	0	1
1	1	0

Например, (1010) (0110)=(1100); (1010) (0110)=(0010).

Операции и − алгебраические, нейтральный элемент – нулевая битовая строка (0…0). Для каждой битовой строки противоположным элементом является эта же битовая строка. Доказательство коммутативности, ассоциативности операций и и дистрибутивность логического умножения относительно операции сводятся к доказательству этих свойств для битовых строк длиной 1, которое проводится прямыми вычислениями. Т.о., пространство битовых строк с операциями , является кольцом, которое обозначается . Это кольцо является ассоциативным кольцом с единицей.

Так как (;+) абелева группа, то противоположный элемент . Поэтому в К можно ввести операцию вычитания: .В силу свойства группы единственное решение уравнения .