7О. Однородные системы уравнений.
Рассмотрим однородную систему уравнений:
Лемма 1. Система однородных уравнений всегда совместна.
Really
– ее решение. Это решение называется
тривиальным.
Ненулевые решения называются нетривиальными.
В соответствии с общей теорией, справедлива следующая лемма.
Лемма 2.
Однородная система с квадратной матрицей
имеет нетривиальное решение
.
Доказательство.
Пусть нетривиальное решение существует,
тогда два решения. Методом от противного.
Пусть
по формулам Крамера – решение единственное,
что противоречит условию
.
Следовательно,
существуют свободные переменные
нетривиальное решение.
Теорема 5. (о множестве решений системы однородных уравнений).
Множество
решений СОЛУ образует в пространстве
подпространство размерности
,
где
.
Доказательство. В соответствии с п.4о, решение СОЛУ можно записать в виде (см. формулу (7)):
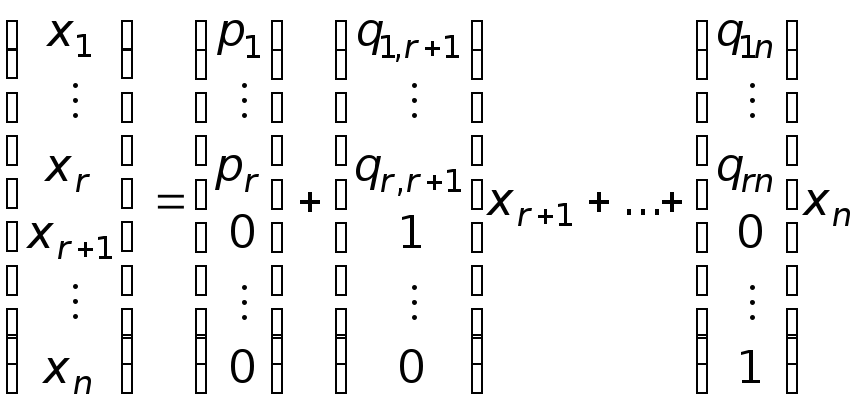
т.к.
,
т. е. в случае СОЛУ, любое решение системы
выражается в виде линейной комбинации
векторов:
,
…,
.
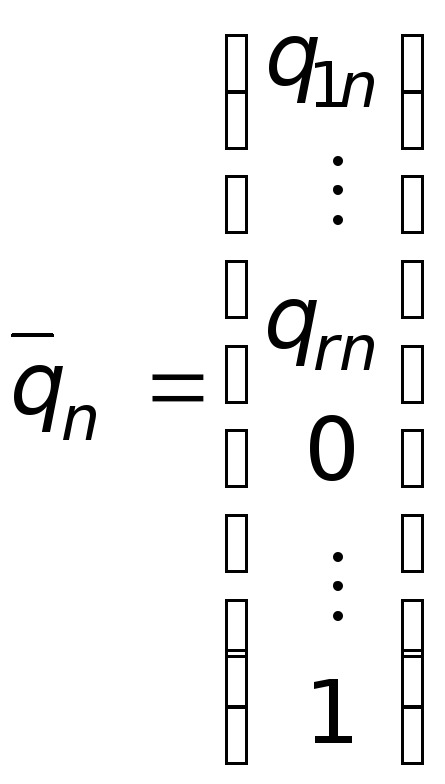Следовательно,
множество всех решений СОЛУ образует
подпространство в пространстве
.
Теперь
покажем, что вектора
– линейно независимы. Для этого составим
матрицу
из их координат:
Снизу
расположен минор порядка
,
отличный от нуля
столбцов матрицы
линейно независимы
вектора
– линейно независимы
эти вектора образуют базис подпространства
размерность подпространства равна
.
ч.т.д.
Пусть
известны какие-либо
линейно независимых решений СОЛУ:
,
…,
.
Тогда, в силу предыдущей теоремы, эти вектора образуют базис в подпространстве всех решений СОЛУ и любое решение может быть представлено в виде линейной комбинации этих векторов
,
. (11)
и обратно, любая линейная комбинация дает решение СОЛУ.
Def 9.
Всякая линейно независимая система
решений СОЛУ (1) называется фундаментальной
системой решений.
Т.о.,
для того, чтобы решить СОЛУ, надо найти
фундаментальную систему решений. Тогда
общее решение задается формулой (11), где
– произвольные элементы
.
Пример.
;
.
,
.
.
Теперь
покажем, что любое подпространство
пространства
может быть получено как решение некоторой
СОЛУ.
Теорема
6. Всякое
подпространство
размерности
в пространстве
с данным базисом является подпространством
решений некоторой системы линейных
однородных уравнений ранга
.
Доказательство.
Пусть в
задан базис
и подпространство
.
Возьмем в
базис
дополним его до базиса в
:
.
Каждый вектор
можно разложить оп этому базису
,
причем
,
т.к.
– линейная оболочка
.
Уравнения
,
…,
определяют
в базисе
.
Известно, что два базиса связаны
формулами:
,
где
– матрица перехода,
.
Тогда
– формула связи координат вектора в
различных базисах. Следовательно,
и система уравнений на
имеет вид
,
(12)
Т.к.
строки матрицы
линейно независимы
ранг системы (12) равен
.
ч.т.д.
8О. Системы линейных неоднородных уравнений
Рассмотрим систему неоднородных уравнений
(13)
Пусть
.
Пусть
– решение этой системы, т.е.
(14)
Вычитая из (13) выражение (14), получаем
.
Т.о.,
является решением соответствующего
однородного уравнения.
Пусть
– фундаментальная система решений
однородного уравнения. Тогда любое
может быть представлено в виде:
.
Тогда получаем
(15)
Если
– частное решение уравнения (13), то
формулы (15) дают общее решение. Из (15)
следует теорема.
Теорема 7. Общее решение СЛНУ (13) представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы.
Следствие 1. Разность двух произвольных решений СЛНУ является решением соответствующей СЛОУ.
Следствие 2. Сумма любого частного решения СЛНУ с любым частным решением соответствующей СЛОУ дает частное решение СЛНУ.
Замечание.
В формуле (7) вектор
– частное решение СЛНУ, а вектора
– частные решения СЛОУ.