5. Метод Гаусса решения слу.

На практике чаще всего используют метод Гаусса построения решений СЛУ. При этом при исследовании и решении СЛУ производятся элементарные преобразования строк расширенной матрицы : перестановка строк (это соответствует перестановке уравнений системы), сложение строк (это соответствует сложению уравнений системы), умножение строк на отличное от нуля число (это соответствует умножению уравнения системы на отличное от нуля число). Очевидно, что при указанных преобразованиях получается система, эквивалентная данной. Следовательно, после элементарных преобразований строк расширенной матрицы получается расширенная матрица некоторой новой системы, эквивалентной данной системе.

Замечание. Перестановка в основной матрице двух столбцов соответствует в системе перестановке неизвестных вместе со своими координатами. Умножение столбца на число и сложение столбцов приводит к изменению коэффициентов только при одном неизвестном и значит к системе, не эквивалентной рассматриваемой.

Рассмотрим матрицу . Элементарными преобразованиями строк ее можно привести к ступенчатой матрице : :

( – некоторый элемент поля ). .

Выберем в матрице ненулевой минор порядка , т.е. базисный минор. Как и в теореме 11, §11 (о ступенчатой матрице), его можно выбрать на пересечении первых строк и столбцов, с которых начинаются ненулевые элементы строк. Этот минор верхнетреугольный и равен произведению . Будем считать, что этот минор расположен в левом верхнем углу матрицы (перестановкой столбцов матрицы и перенумерацией переменных этого всегда можно добиться). Нулевые строки матрицы отбросим (этому соответствуют уравнения с любым решением).

.

Далее все элементы базисного минора выше главной диагонали можно сделать равными нулю (как в теореме 11, §11), а элементы главной диагонали – равными 1 (умножением строки на ):

Т.о., исходная система (1) приведена к эквивалентной системе

или к системе

Отсюда видно, что если , то система имеет единственное решение

, …, .

Если , то переменные – базисные, – свободные и придавая им произвольные значения , …, , получим решение:

(9)

или, по аналогии с (7)

(10)

По аналогии с п.4 можно показать, что (9), (10) дают общее решение системы (1).

Итак, метод Гаусса состоит в следующем.

1. расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду;

2. сравнивают ранги основной и расширенной матриц и делают вывод о совместности или не совместности системы;

3. в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице;

4. выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть;

5. если ,то в правой части стоят только свободные члены и получено единственное решение;

6. если , то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (9).

Пример (см. п.4).

  

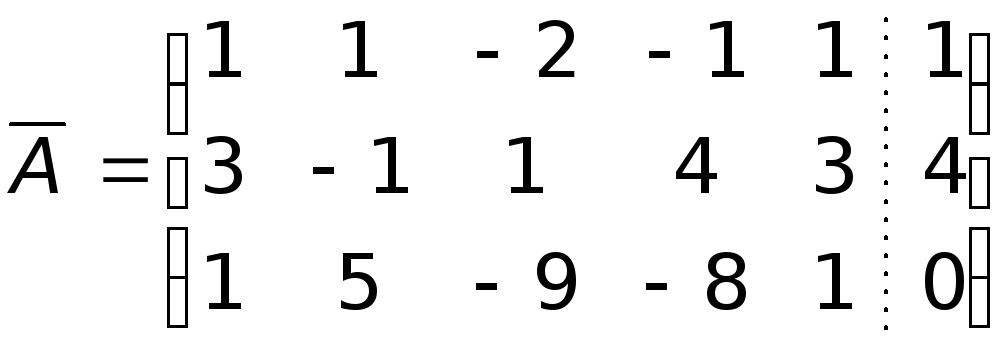
6. Нахождение обратной матрицы методом Гаусса.

Напомним, что матрица называется обратной к , если . Обратные матрицы существуют лишь для невырожденных матриц, т.е. . Было показано, что , где – присоединенная матрица, полученная из алгебраических дополнений, т. е. вычислением определителей -ого порядка. Вместе с тем, операция вычисления определителя, запрограммированная в ЭВМ, требует больших машинных ресурсов. Поэтому более предпочтительным выглядит вычисление обратной матрицы с помощью метода Гаусса.

Для этого воспользуемся определением обратной матрицы

…

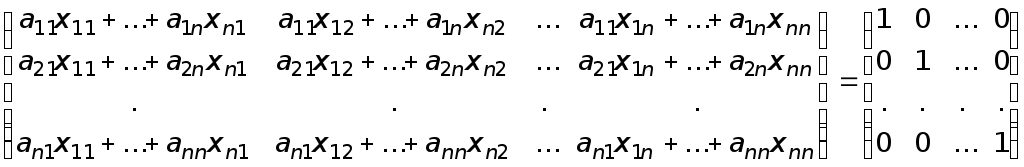
Т.о., матричное уравнение эквивалентно системе линейных уравнений, состоящей из систем, каждая из которых является системой из переменных и все они имеют одну и ту же основную матрицу систем:

; ; …;

Все эти системы объединим в одной расширенной матрице:

Приведение этой матрицы к ступенчатому виду должно обозначать приведение к ступенчатому виду всех расширенных матриц подсистем. Так как она может быть приведена к следующему виду

Решение каждой из подсистем имеет вид:

, , …,

матрица , стоящая за вертикальной чертой, является обратной матрицей .

Пример (см. пример из §8)

    