ЛЕКЦІЯ № 24(5.5)

З ДИСЦИПЛІНИ

« ПРИКЛАДНА КРИПТОЛОГІЯ»

Тема лекції

«Електронні цифрові підписи з відновленням повідомлень.

Аналіз основних властивостей»

Навчальні питання

24.1(5.5.1) Цифровий підпис Міяджі з відновленням повідомлення в групі точок еліптичної кривої (Elliptic Curve Miyaji message recovery signature (ECMR))

24.2(5.5.2) Цифровий підпис Абі-Окамото з відновленням повідомлення в групі точок еліптичної кривої (Elliptic Curve Abe-Okamoto message recovery signature (ECAO))

24.3(5.5.3). Цифровий підпис Пінтсова-Ванстона в групі точок еліптичних кривих (Elliptic Curve Pintsov-Vanstone (ECPV) message recovery sig Б

24.4.(5.5.4). Цифровий підпис KC-DSA в групі точок еліптичної кривої

24.5.(5.5.5)(Elliptic Curve KC DSA/Nurberg-Rueppel (ECKNR) message recovery signature)

Завдання до самостійної роботи

Відпрацювакти пункти 24.1 – 24.5

Джерела що рекомендуються для самостійної робот

Джерела, що рекомендуються до самостійної роботи

1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія (електронний варіант). Розд 6. Харків, ХНУРЕ, 2011 р.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. (ЛК №18). Харків, ХНУРЕ, 2011 р.

3. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

4. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.

Додаткова література

1.В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.

2. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с

3. Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с

4. Закон України « Про електронний цифровий підпис»

24.1 Цифровий підпис Міяджі з відновленням повідомлення в групі точок еліптичної кривої (Elliptic Curve Miyaji message recovery signature (ecmr))

Цифровий підпис ECMR засновано на схемі підпису, яку визначено в [46, 12, 342]. Розглянемо її детально за етапами.

Доменні параметри та параметри користувача

Ключі для ECMR формуються таким чином:

1) генерується або вибирається особистий (довгостроковий) ключ підпису об’єкта , причому – випадкове ціле число з інтервалу ;

2) обчислюється відкритий ключ перевірки цифрового підпису об’єкта (спосіб I або спосіб II).

Об’єкт також вибирає геш-функцію:

Процес обчислення (генерації) підпису

Вхідні дані для процесу генерації підпису повинні містити:

– доменні параметри ЕС;

– особистий ключ цифрового підпису ;

– дані з доданою або природною надлишковістю у вигляді .

Дані формуються з повідомлення [46, 12]. Виходом 2роцессу генерації підпису є пара , що є цифровим підписом для даних.

Цифровий підпис даних об’єкт А має виконувати в такій послідовності.

Генерація ключа сеансу й попереднього підпису

1. Обрати (генерувати) випадкове ціле з інтервалу .

2. Обчислити точку еліптичної кривої , де Р – базова точка порядку п.

Обчислення за модулем порядку п групи G:

1. Визначити передпідпис як .

2. Обчислити першу складову підпису .

3. Обчислити другу складову підпису .

4. Знищити .

Якщо або , то процес генерації підпису має бути повторено з новим випадковим значенням .

Форматування підписаного повідомлення

Пара є підписом об’єкта для даних .

Перевіряння підпису

Вхідні дані для процесу перевіряння підпису повинні містити:

– доменні параметри EK;

– відкритий ключ перевірки об’єкта ;

– одержаний підпис для , представлений двома цілими числами та ;

– не відновлюване повідомлення (за наявності).

Для перевірки підпису об’єкта для об’єкт повинен виконати такі кроки.

Перевіряння розміру підпису

Перевірити, що та , та . Якщо хоча б одна з умов не виконується, то відхилити підпис.

Відновлення попереднього підпису (у групі точок еліптичної кривої)

1. Обчислити .

2. Обчислити .

Відновлення вхідних даних або повідомлення

Обчислити .

Зіставлення підпису

Зіставлення надлишковості має здійснюватися за умови, що надлишковість обчислена і відома перевірнику. Якщо = d, то вважається, що повідомлення цілісне й справжнє, інакше робиться відхилення прийнятого повідомлення (підпису).

Таким чином, схема використовує функції маскування та гешування з однаковою довжиною та n-бітовою довжиною результату.

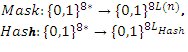
При обчисленні передпідпису П необхідно виконати такі умови:

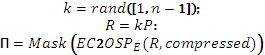
При обчисленні відновлюваного цифрового підпису дані маскуються передпідписом за допомогою складання за модулем 2, а обчислення s необхідно виконати згідно з нижче наведеним:

При перевірянні підпису необхідно виконати умови щодо представлення даних у ході обчислень:

24.2Цифровий підпис Абі-Окамото з відновленням повідомлення в групі точок еліптичної кривої (Elliptic Curve Abe-Okamoto message recovery signature (ecao))

Цифровий підпис ECAO засновано на схемі підпису, яка визначена в [46, 336, 12]. Розглянемо її детально за етапами, визначеними в [12,46].

Доменні параметри та параметри користувача

Асиметрична пара ключів для ECAO формуються таким чином.