1.1. Вычисление коэффициентов математической модели

Для составления матриц ПФЭ можно использовать следующие правила:

1) Правило двоичного счета (составляется в соответствии «0»-минус, «1»-плюс).

2) Плюс и минус изменяются в i-ом столбце с шагом 2^m-i.

Второй метод более удобен для программного составления матриц ПФЭ.

Нормированная матрица ПФЭ обладает следующими полезными свойствами:

1. Свойство ортогональности: , .

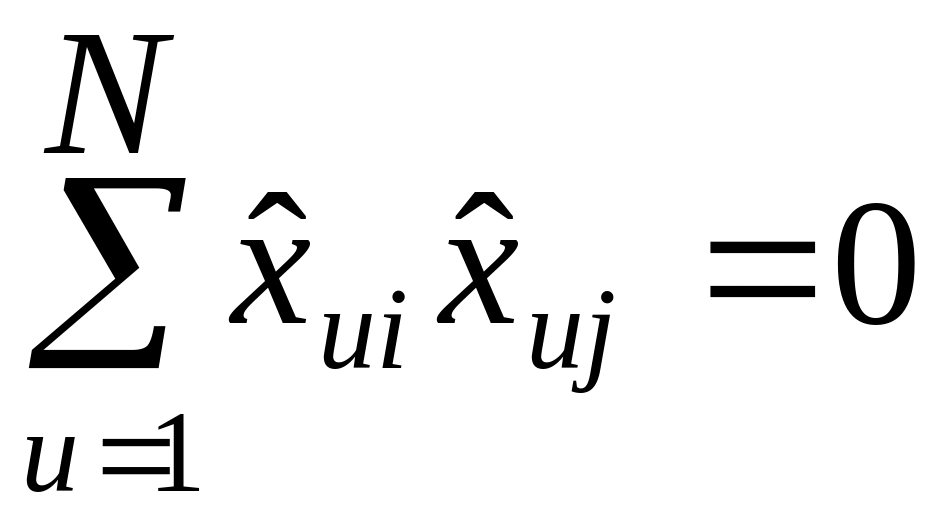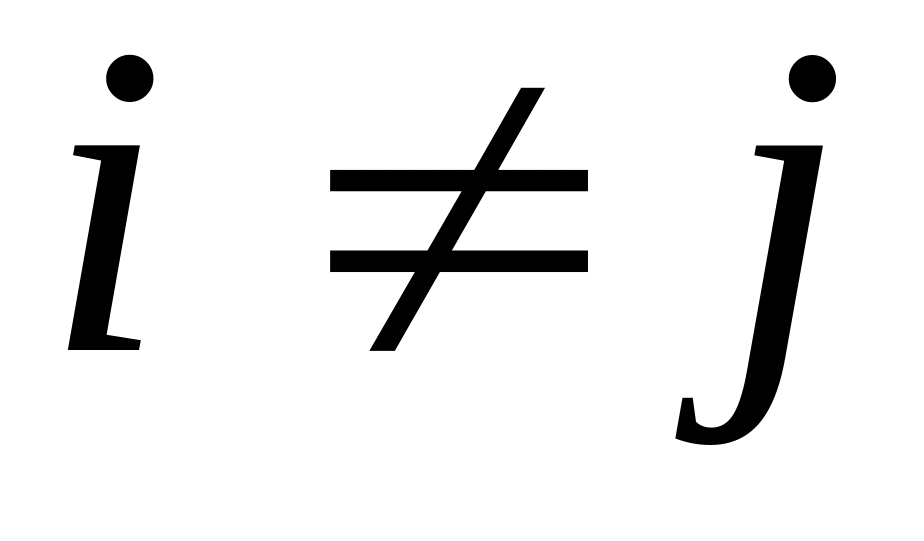Благодаря этому свойству существенно упрощаются формулы для расчета коэффициентов функции отклика с использованием метода наименьших квадратов (МНК).

2) Свойство нормировки:

3) Свойство симметрии:

Второе и третье свойства обусловлены тем, что каждая переменная устанавливается одинаковое количество раз на верхнем и нижнем уровнях, это обеспечивает одинаковую достоверность оценки их влияния на Y. По результатам ПФЭ коэффициенты функции отклика определяются по следующим формулам, вытекающим из МНК:

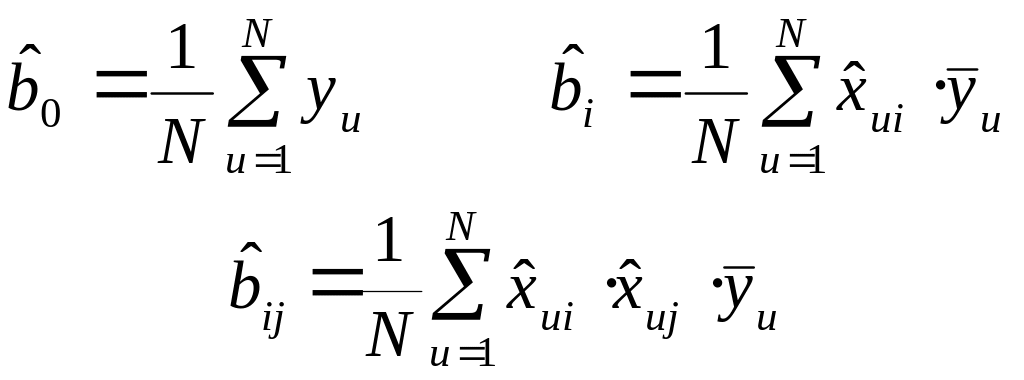(3)

Эти коэффициенты справедливы для уравнения, в котором фигурируют нормированные входные переменные. Эти нормированные значения (+1 и -1) подставляются в формулы (3). А на реальный объект в ходе эксперимента подаются соответствующие натуральные значения.

Для получения полинома с ненормированными факторами, достаточно в уравнении (1) раскрыть нормированные значения по формуле (2).

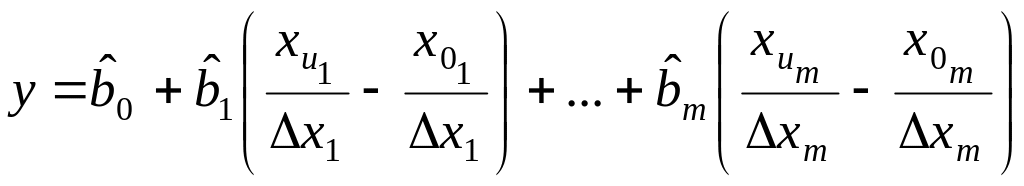(4)

.

Адекватность модели (1) и значимости его членов оценивают по критериям Фишера и Стьюдента.

1.2. Оценка значимости коэффициентов модели

Значимость i-того коэффициента оценивают по критерию Стьюдента:

, (5)

где - i-тый коэффициент в уравнении с нормированными переменными;

- дисперсия воспроизводимости, которая характеризует ошибку измерений и может быть вычислена по результатам l повторных измерений выхода y:

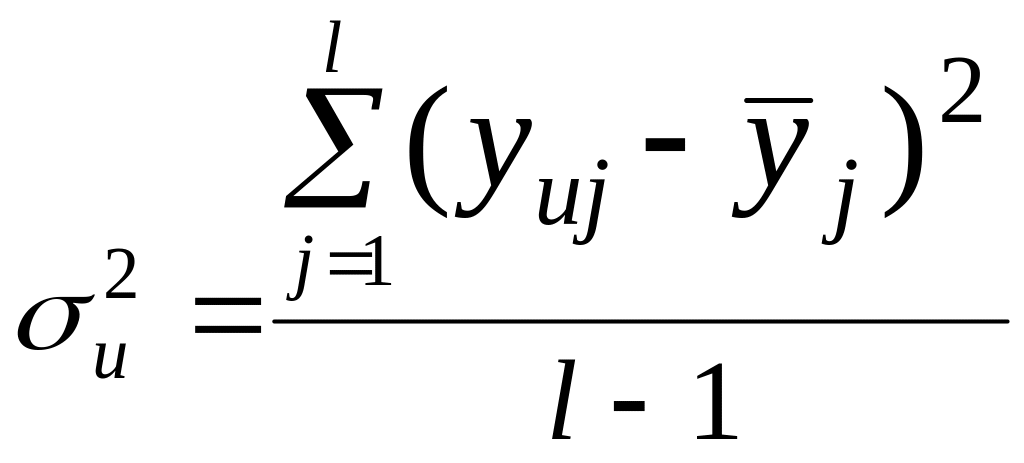, (6)

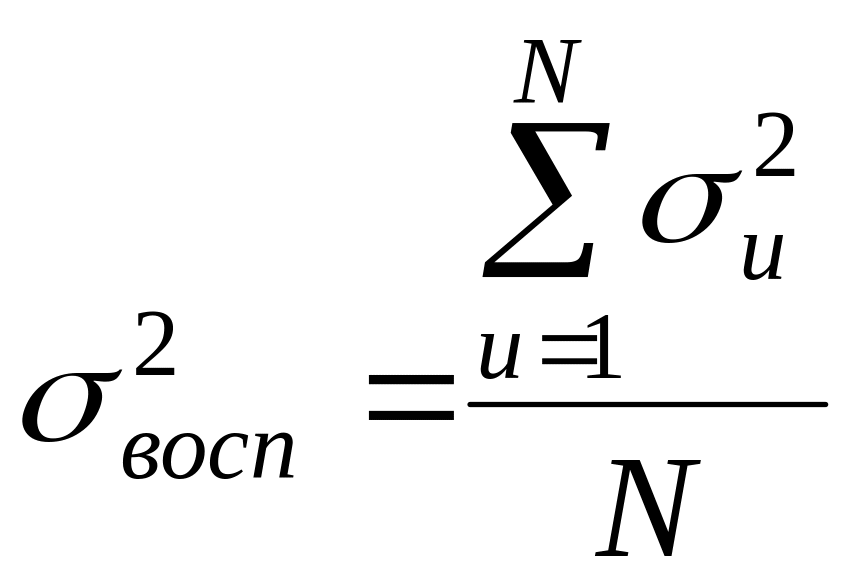, (7)

где - значение выхода, измеренное в u-том опыте и j-том повторном измерении; - среднее значение выхода по l измерений в u-том опыте.

Если , то i-тый коэффициент считается незначимым и может быть опущен.

- критическое значение коэффициента Стьюдента, которое берется из таблицы (приложение 2) в зависимости от , принятого уровня значимости  =0,95.

1.3. Оценка адекватности модели

В заключении проверяется адекватность полученного уравнения регрессии по критерию Фишера, который чаще всего определяется по формуле:

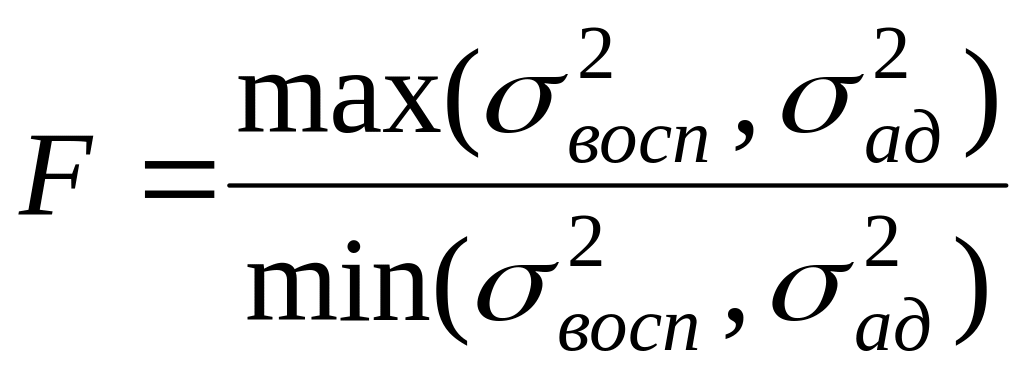(8)

если , то 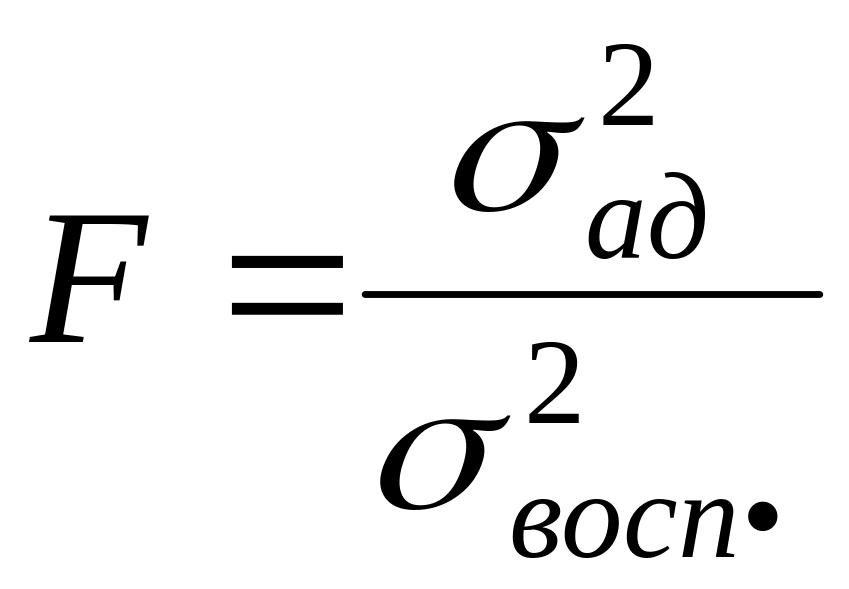, - дисперсия адекватности (остаточная дисперсия), характеризующая ошибку модели:

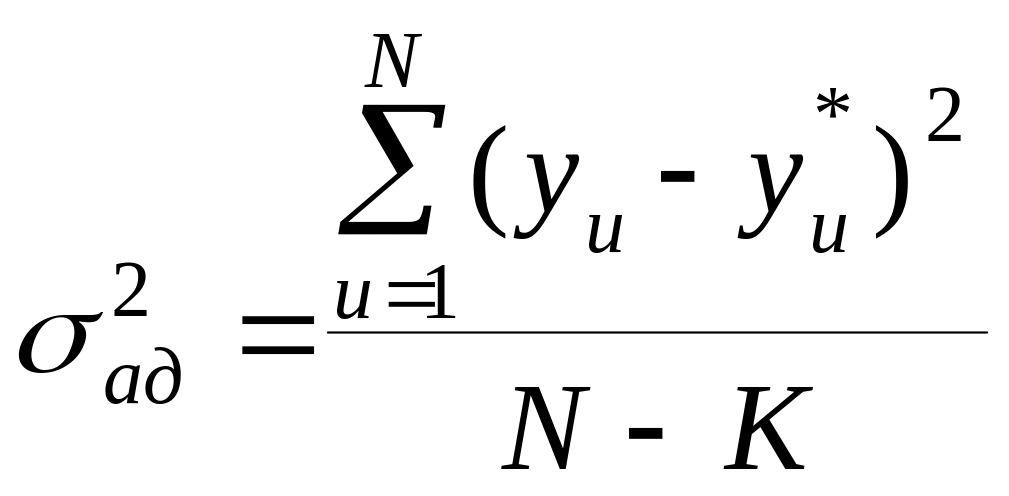, (9)

где - значение, вычисленное по модели; К - количество искомых коэффициентов регрессии, - количество степеней свободы дисперсии адекватности равное количеству дополнительных опытов, не использованных для вычисления коэффициентов регрессии, а использованное для проверки адекватности.

Если , то модель считается адекватной, где F_кр – критическое значение критерия Фишера, которое берется из таблицы (приложение 3) в зависимости от , и .