Вариант 1 Теория функций комплексного переменного
1. Решите уравнение
.
2. Вычислите комплексное число
.
3. Найдите мнимую и действительную части
функции
.
4. Проверить выполнение условий Коши-Римана и в случае их выполнения
найти производную функции
.
5. Восстановить аналитическую функцию по заданной её действительной или
мнимой части:
;
.
6. Вычислить интеграл по
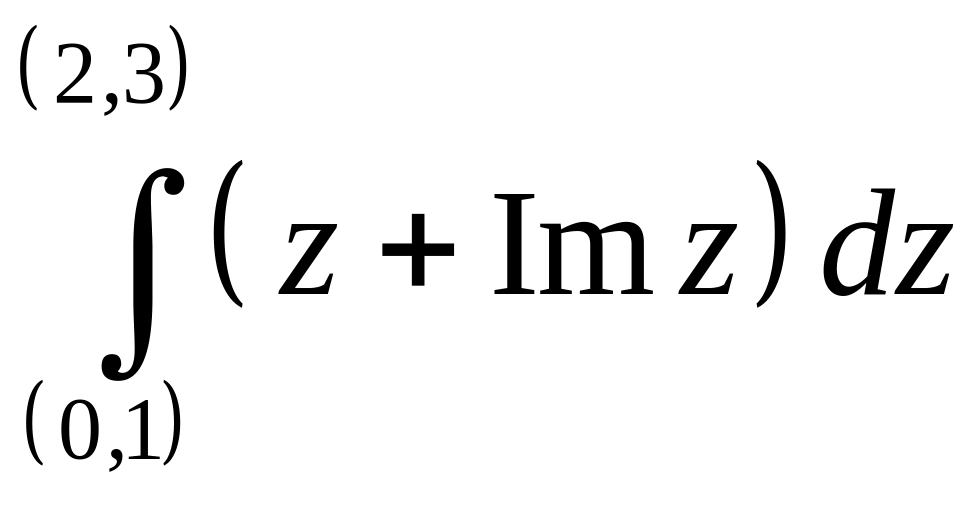, по
прямой, соединяющей точки.
7. Вычислить интеграл
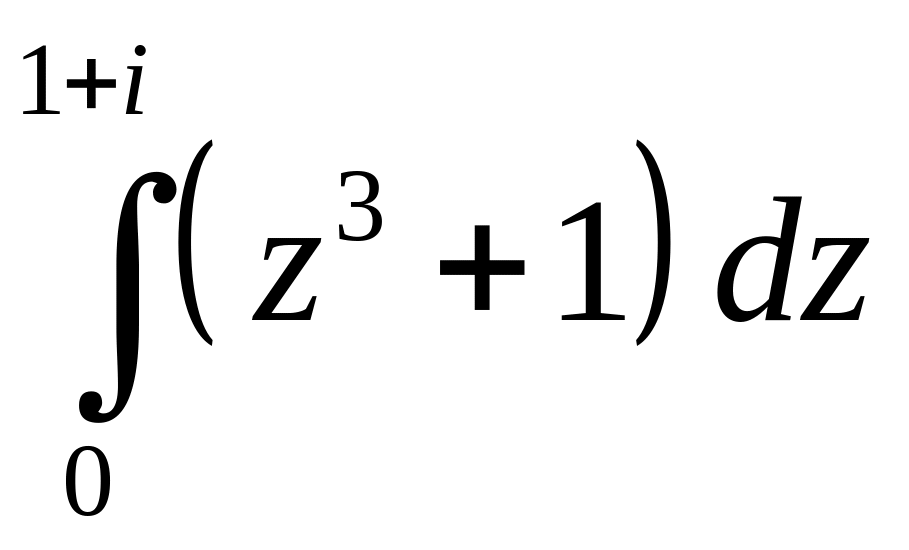по отрезку прямой.
8. Найти все особые точки заданной функции, определить их характер и найти
вычеты в них. Установить, чем является для данной функции бесконечно уда-
ленная точка, и найти вычеты в ней
.
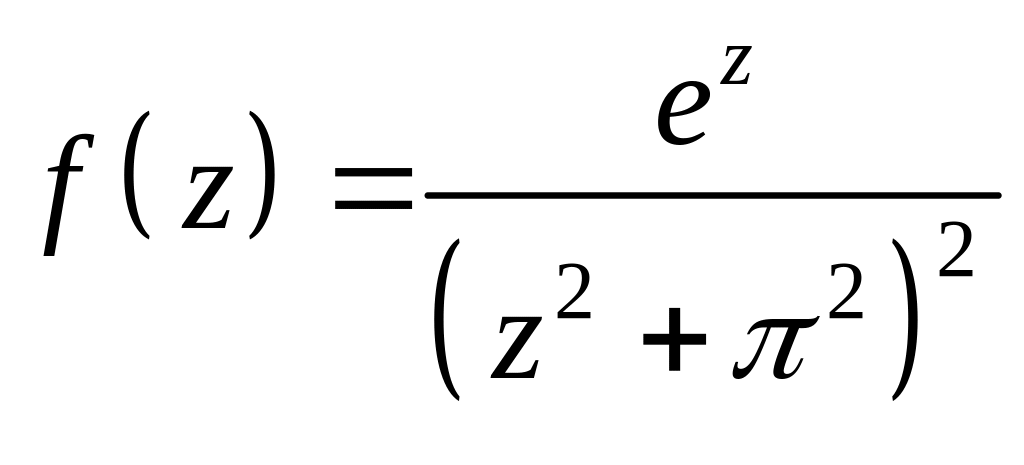9. Вычислить интеграл по замкнутому контуру, используя основную теорему
о вычетах или интегральную теорему Коши, или формулу для производных
высших порядков
,
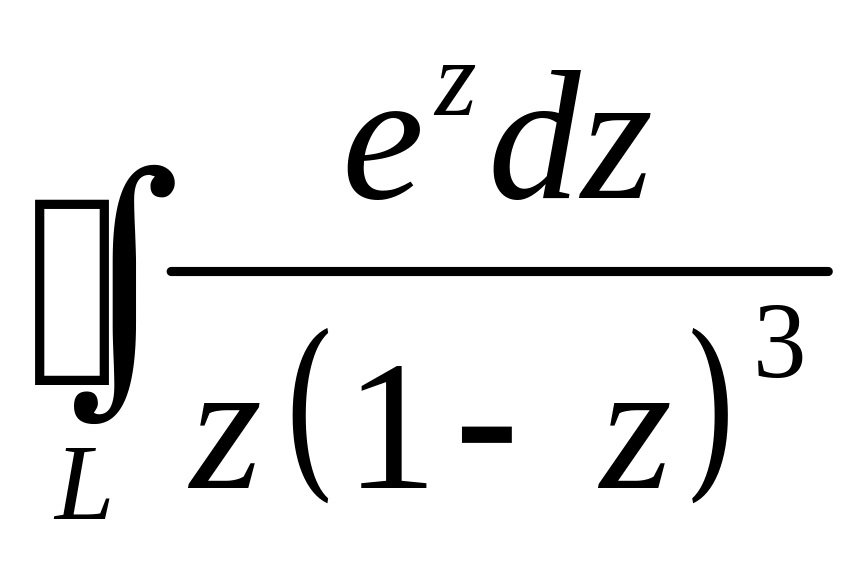где
– окружность
.
10. Вычислить интеграл от функции
действительного переменного
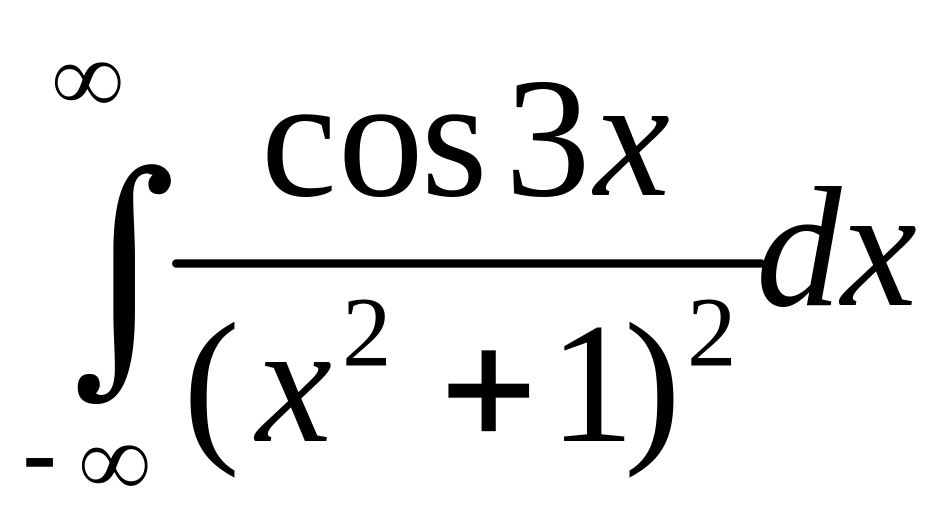
11. Разложить функцию
в ряд Лорана в области
.
12. Найдите образ линии
при отображении
,
где
;
:
.
13. Найти изображение:
14. Решить дифференциальные уравнения операторным методом:
а)
,
при
,
.
б)
,
при
,
.
Вариант 2 Теория функций комплексного переменного
1. Решите уравнение
.
2. Извлечь корень соответствующей степени
из данного числа:
.
3. Найдите мнимую и действительную части
функции
.
4. Проверить выполнение условий Коши-Римана и в случае их выполнения
найти производную функции
.
5. Восстановить аналитическую функцию по заданной её действительной или
мнимой части:
;
.
6. Вычислить интеграл по заданному пути
интегрирования
,
где
отрезок действительной оси от точки
до точки
.
7. Вычислить интеграл от аналитической
функции
.
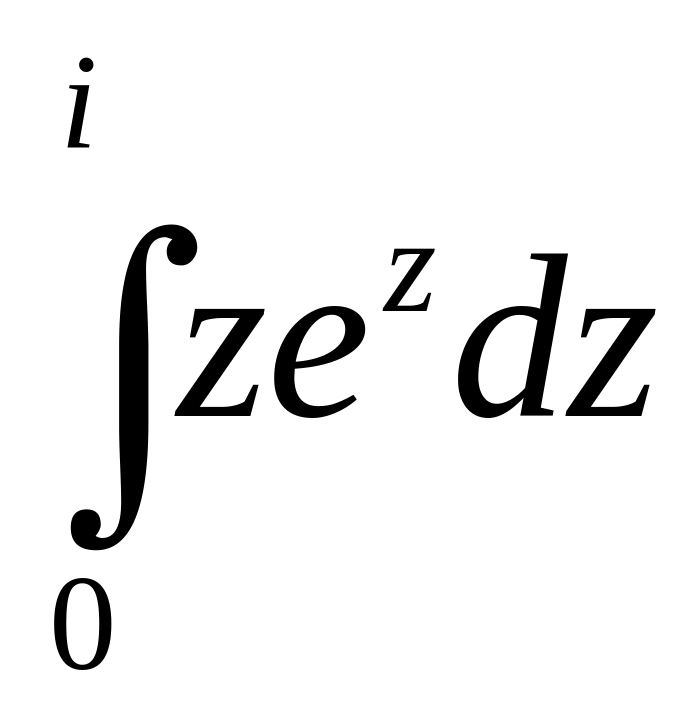8. Найти все особые точки заданной функции, определить их характер и найти
вычеты в них. Установить, чем является для данной функции бесконечно уда-
ленная точка, и найти вычеты в ней
.
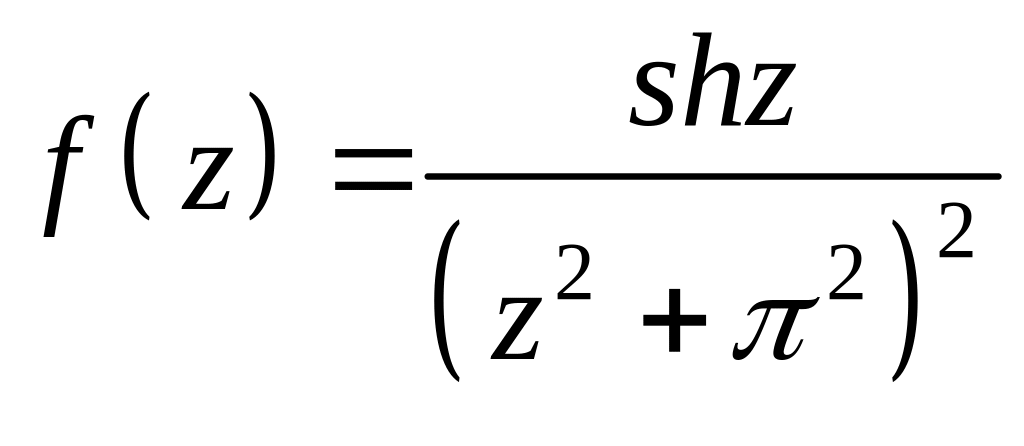9. Вычислить интеграл по замкнутому контуру, используя основную теорему
о вычетах или интегральную теорему Коши, или формулу для производных
высших порядков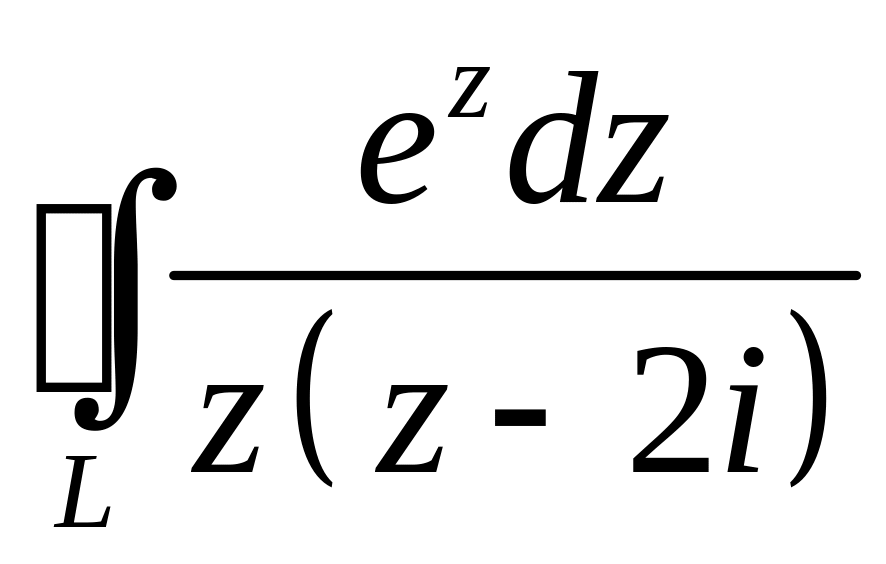
,
где
– окружность
.
10.Вычислить интеграл от функции действительного переменного
.
11. Разложить функцию
в ряд Лорана в окрестности
.
12. Найдите образ линии при отображении , где ;
:
13. Найти оригинал:
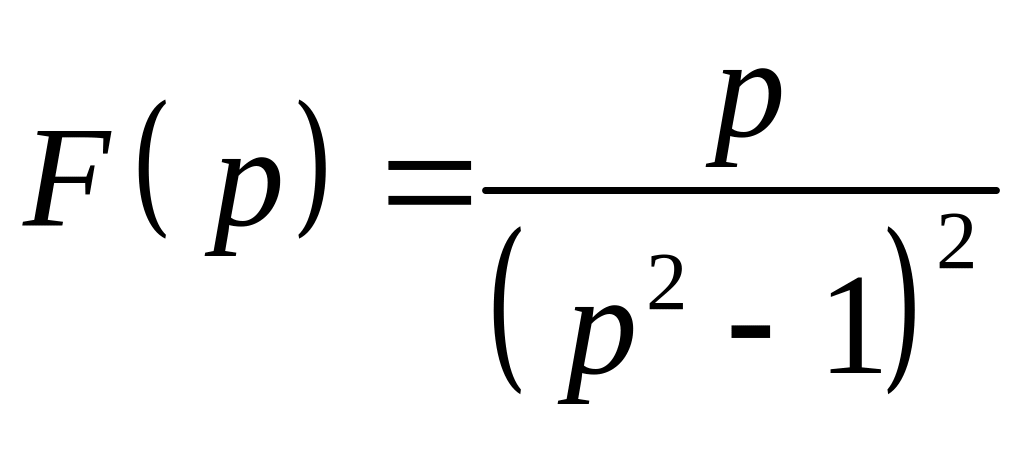
14. Решить дифференциальные уравнения операторным методом:
а)
,
при
,
.
б)
,
при
,
.
Вариант 3 Теория функций комплексного переменного
1. Решите уравнение
.
2. Вычислите комплексное число
.
3. Найдите мнимую и действительную части
функции
.
4. Проверить выполнение условий Коши-Римана и в случае их выполнения
найти производную функции
.
5. Восстановить аналитическую функцию по заданной её действительной или
мнимой части:
;
.
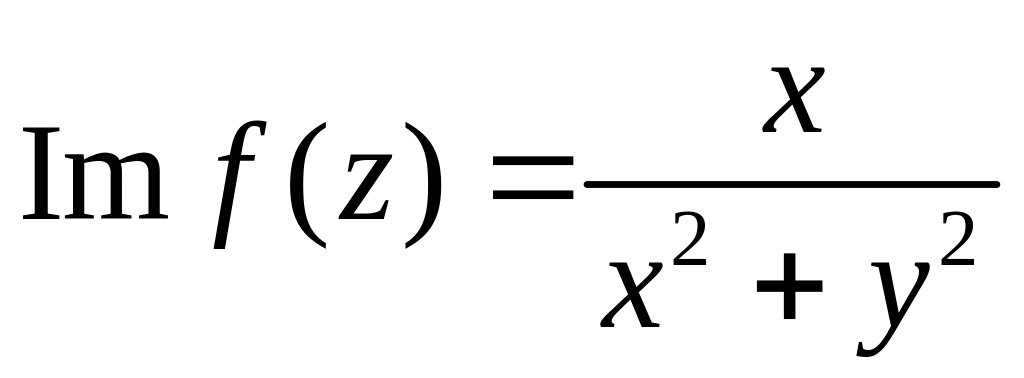6. Вычислить интеграл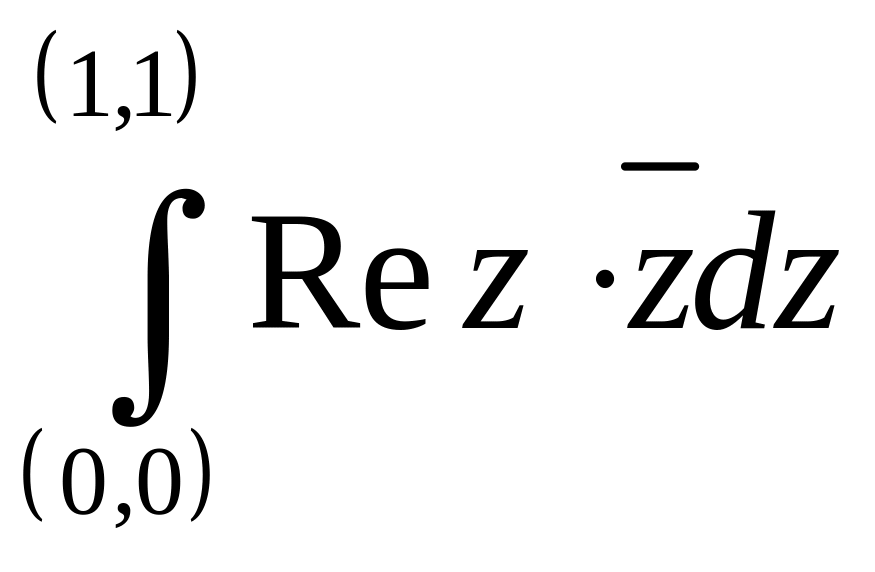 
по
четверти окружности
.
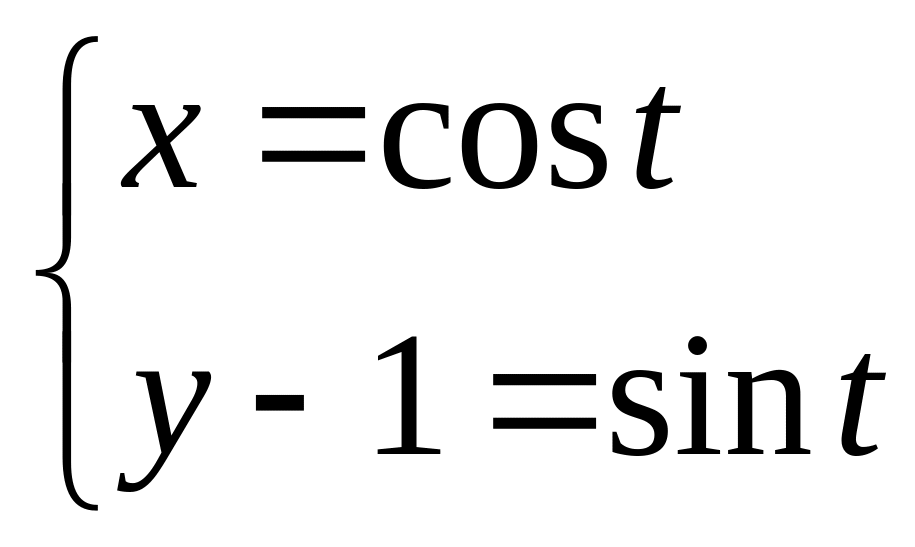7. Вычислить интеграл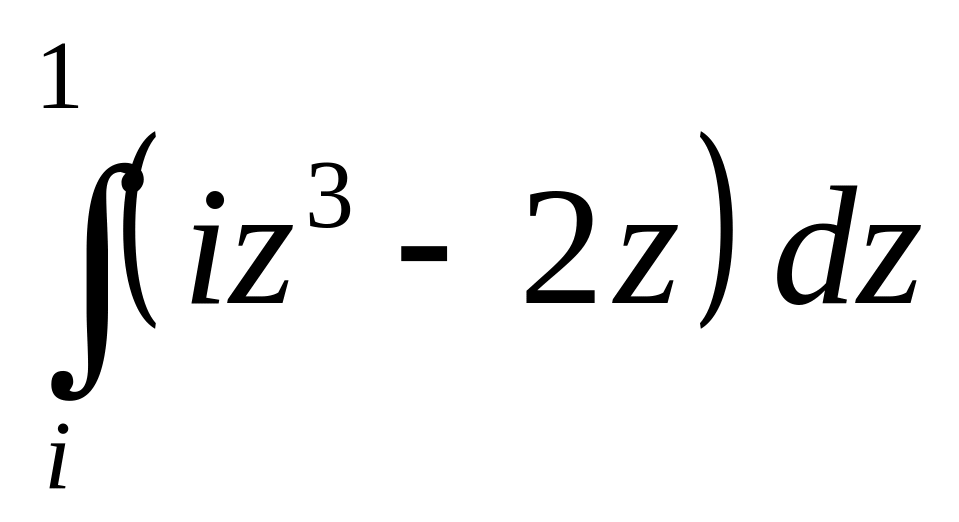 
по отрезку прямой.
8. Найти все особые точки заданной функции, определить их характер и найти
вычеты в них. Установить, чем является для данной функции бесконечно уда-
ленная точка, и найти вычеты в ней
.
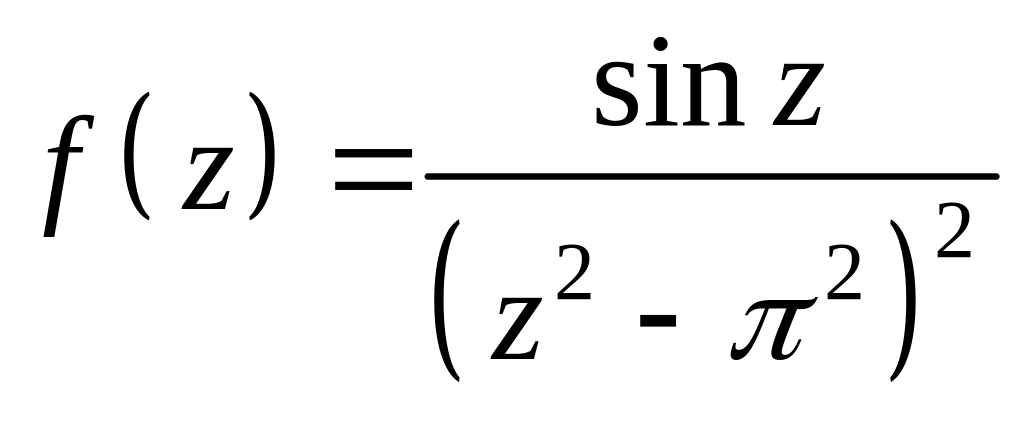9. Вычислить интеграл по замкнутому контуру, используя основную теорему
о вычетах или интегральную теорему Коши, или формулу для производных
высших порядков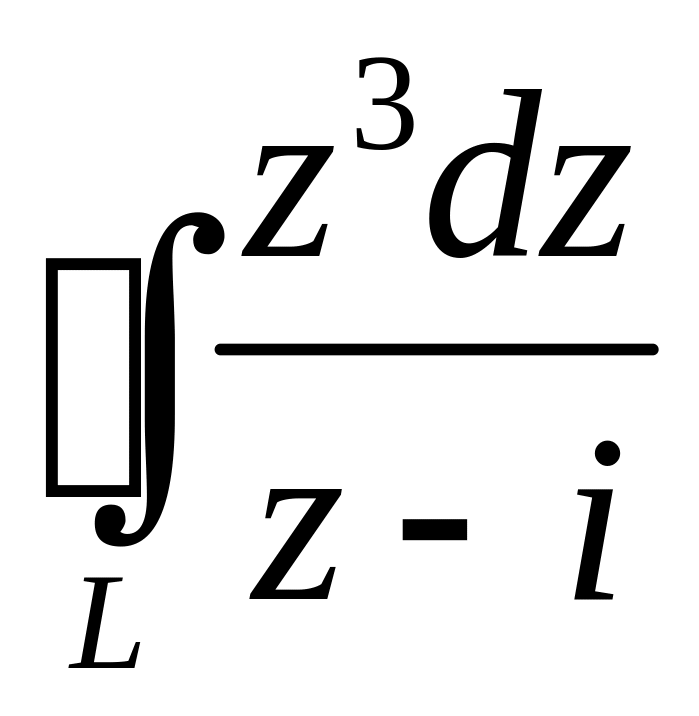
,
где
окружность
.
10. Вычислить интеграл от
функции действительного переменного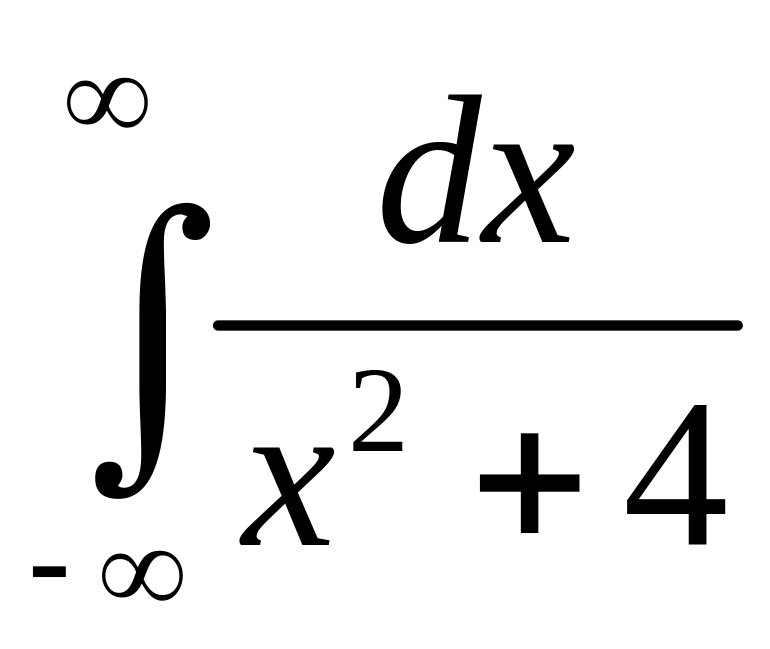
.
11. Разложить функцию
в ряд Лорана в области
.
12. Найдите образ линии
при отображении
,
где
;
:
.
13. Найти изображение:
14. Решить дифференциальные уравнения операторным методом:
а)
,
при
,
.
б)
,
при
.