7.2.2. Математические модели химических реакторов идеального вытеснения
С достаточным приближением МИВ соответствует структуре потока в трубчатых проточных аппаратах при турбулентном движении потоков и больших отношениях длин труб к их диаметрам (L/d > 100).
Построение модели реактора идеального вытеснения проведем для реального трубчатого реактора, удовлетворяющего указанным требованиям. При этом целесообразно записать искомую модель в виде дифференциального уравнения, которое описывает распределение вещества в реакционной среде как за счет гидродинамических факторов, так и за счет химического превращения
. (7.23)
Аналогичные уравнения можно записать для всех участвующих в реакции веществ. В результате получим модель процесса в реакторе вытеснения с учетом изменения переменной cj во времени, т.е. динамическую модель.
Для установившегося режима работы реактора, когда dc/dt = 0, уравнение (7.23) описывает статистику процесса и после замены r = – rA (А – исходное вещество) принимает следующий вид
. (7.24)
Известно, что линейная скорость U = v/S, а элемент длины dz = dV/S. Тогда
. (7.25)
В результате интегрирования уравнения (7.25) получаем:
. (7.26)
Уравнение (7.26) является статической моделью реактора идеального вытеснения в общем виде.
Рассмотрим примеры аналитического решения модели (7.26) для некоторых частных случаев.
С этой целью рассмотрим изотермический реактор идеального вытеснения, в котором химическая реакция в движущемся потоке газа или жидкости протекает при постоянном объеме.
Простая элементарная реакция:
k
A S.
Подставляя значения скорости – rA = kcA в уравнение статической модели реактора идеального вытеснения и интегрируя, получим
(7.27)
или
. (7.28)
Известно, что cА = cА0 (1 – xА). Тогда
. (7.29)
В результате преобразования уравнения (7.28) получаем cA = cA0 exp(–k).
Параллельная реакция:
В выражении (7.28) k следует заменить суммой (k1 + k2), т.е.
, (7.30)
или
(7.31)
и
. (7.32)
Чтобы найти расчетную зависимость для определения cS, используем выражение для скорости реакции по продукту S
. (7.33)
Из последнего равенства получаем
. (7.34)
Интегрируя левую часть равенства в пределах от cS0 до cS и правую от нуля до t (при этом принимаем сS0 = 0), получим:
. (7.35)
7.2.3. Каскад реакторов идеального смешения
Рассмотрим каскад реакторов идеального смешения (рис. 7.2).
Рис. 7.2. Каскад реакторов идеального смешения
Описание процесса в каждом реакторе (индекс А у концентрации опустим) имеет вид
, (7.36)
при dci/dt = 0 получим
. (7.37)
Определим суммарное время (пропорционально общему объему реакторов в каскаде), необходимое для достижения некоторого значения cAкон. Очевидно, что значения c1, c2 и т.д. должны находиться в интервале между cА0 и cAкон; тогда суммарное рис-к будет равно площади под ломаной кривой (рис. 7.3). Площадь под каждой «ступенькой» этой ломаной кривой будет равна времени пребывания в соответствующем реакторе каскада.
Рис. 7.3. Зависимость сА от (к определению времени пребывания)
Рассмотрим каскад одинаковых реакторов (т.е. 1 = 2 = …), в которых в стандартных условиях протекает реакция первого порядка
k
A R.
Математически этот процесс описывается алгебраическими уравнениями вида:
, (7.38)
или после преобразований
. (7.39)
Используя решение (7.39), получим последовательность решений:
, (7.40)
,
……………..
, (7.41)
откуда суммарное время контакта
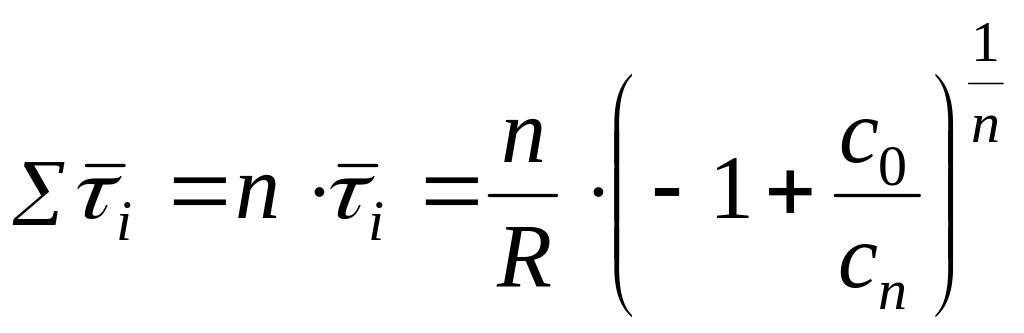, (7.42)
тогда как для РИС
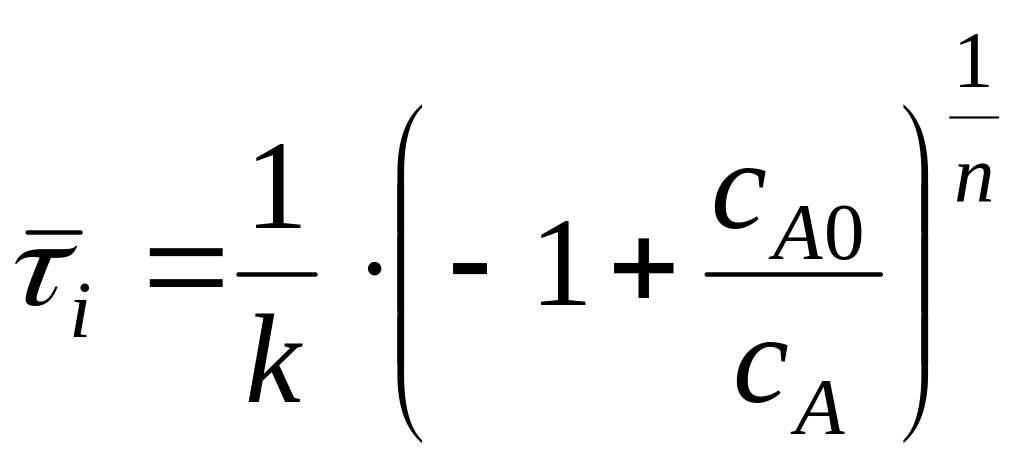. (7.43)