3.2. Экспериментальное изучение распределения времени пребывания элементов потока

Распределение времени пребывания частиц потока (жидкости, газа или сыпучего материала) в аппарате и параметры моделей определяют экспериментальным путем. Для этой цели получили широкое распространение методы нанесения возмущения в определенном сечении потока и фиксирования вызванных им последствий в другом сечении потока. Сигнал может быть различным по форме и по физической природе. Наибольшее распространение получили импульсный и ступенчатый виды возмущений. В качестве сигнала в поток вводят трассер (индикатор, краситель, солевой раствор и т.п.), химически не взаимодействующий со средой и не участвующий в массообмене.

Отклик системы на нанесенное возмущение характеризует распределение времени пребывания частиц потока в аппарате. Функция отклика на возмущение, записанная в безразмерных переменных (концентрация – время), является функцией времени пребывания элементов потока в объеме, ограниченном сечением ввода трассера и замера отклика системы.

3.3. Интегральная и дифференциальная функции распределения времени пребывания элементов потока

В химической технологии для определения функции распределения времени пребывания часто используются два вида возмущения: импульсное (t) (дельта-функция) и ступенчатое 1(t) (единичный скачок). При импульсной подаче трассера на выходе системы получается дифференциальная функция распределения времени прерывания (рис. 3.1). Физически данная форма подачи трассера означает, что на вход аппарата в некоторый момент времени t = t₀ мгновенно подается единичное количество трассера. Одновременно начинают регистрировать концентрацию трассера во времени на выходе аппарата.

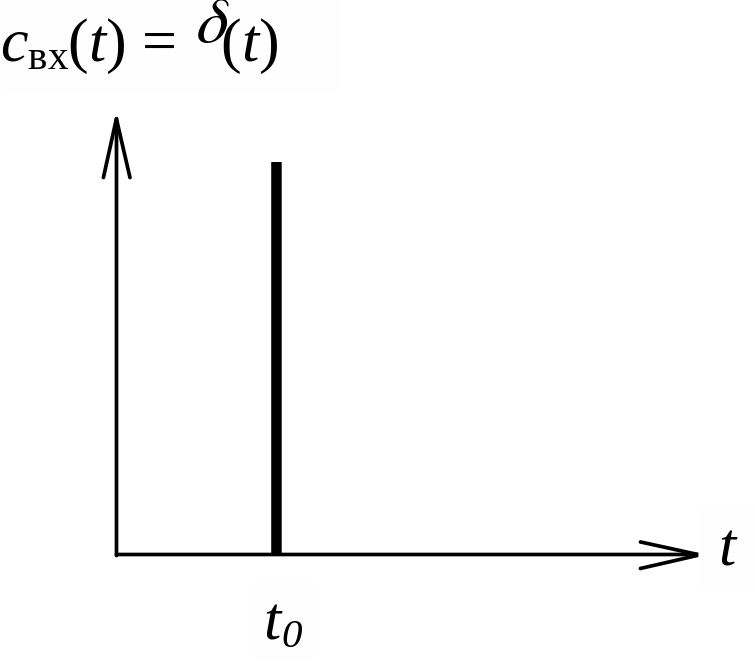
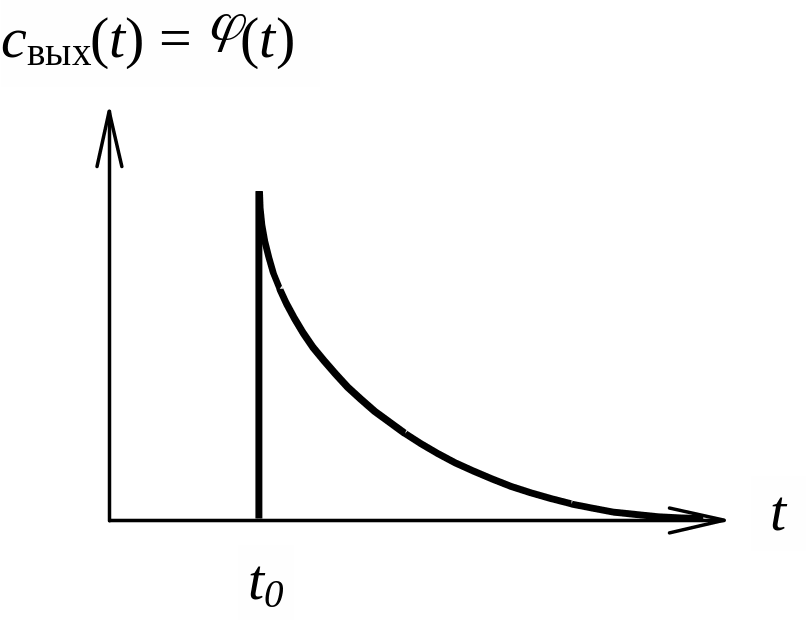
а б

Рис. 3.1. (t) функция (а) и отклик на (t) функцию (б)

При подаче трассера в виде единичного скачка на выходе системы получается интегральная функция распределения времени пребывания (рис. 3.2).

Физически рассматриваемая форма подачи означает, что в момент времени t = t₀ мгновенно включается подача трассера, после чего концентрация на входе аппарата поддерживается постоянной, т.е.

.

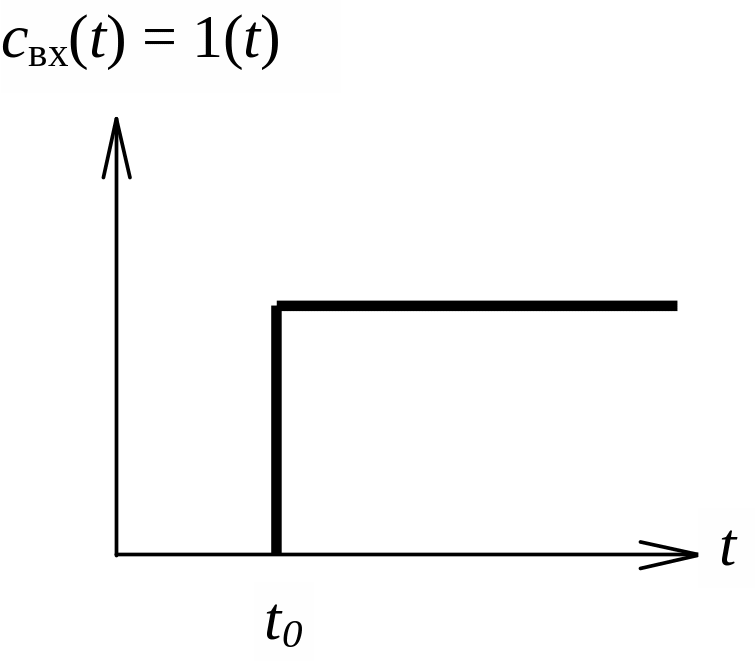
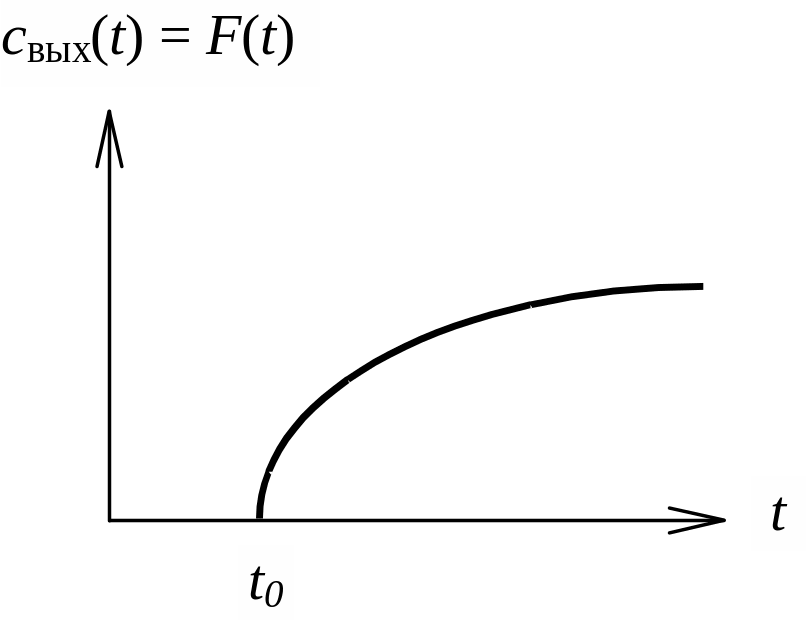
а б

Рис. 3.2. 1(t)-функция (а) и отклик на 1(t) функцию (б)

3.4. Типовые модели структуры потоков

Известно, что структура потока характеризуется степенью перемешивания частиц потока, которая определяет поле концентраций и градиент температуры. Это обстоятельство послужило предпосылкой для установления по характеру перемешивания некоторых типовых моделей гидродинамики потока.

К типовым моделям структуры потоков относится модель идеального смешения (МИС) и модель идеального вытеснения (МИВ). Эти модели теоретические и соответствуют идеальным потокам, однако в ряде случаев их можно использовать для характеристики реальных потоков.

К типовым моделям структуры потоков также относятся диффузионная, ячеечная и комбинированные модели. Эти модели характеризуют реальные потоки и при предельных условиях переходят в одну из теоретических моделей – МИС и МИВ.

3.4.1. Модель идеального смешения

Согласно этой модели принимается, что поступающий в аппарат поток мгновенно распределяется по всему объему вследствие полного перемешивания частиц потока (рис. 3.3). При этом концентрация распределенного вещества во всех точках зоны идеального смешения и в потоке на выходе из него одинакова.

Рис. 3.3. Схематическое изображение аппарата со структурой потока МИС

Изменение концентрации во времени в рассматриваемом потоке в дифференциальной форме запишется следующим образом

. (3.6)

Для заданных начальных условий t = 0, с_t=0 = с₀, где с_вх, с_вых, с – концентрация вещества в потоке соответственно на входе, выходе и в любой точке объеме аппарата, моль/м³; V – объем зоны идеального смешения, м³; v – объемная скорость потока, поступающего в зону идеального смешения и выходящего из него, м³/с; t. – время, с.

Отношение V/v характеризует среднее время пребывания элементов потока в зоне идеального перемешивания; его принято называть средним временем пребывания элементов потока в аппарате и обозначать , оно определяется экспериментально либо расчетным путем.

Уравнение (3.6) с учетом  можно записать в виде

.

МИС есть модель с сосредоточенными параметрами, так как основная переменная с изменяется только во времени.

Искомая функция с(t) может принимать разные значения при различных входных сигналах с_вх(t).

Если с_вх(t) = 1(t) – единичный скачок, то c(t) = F(t), если с_вх(t) = (t) – дельта функция, то c_вых(t) = (t). Для МИС указанные решения имеют вид:

– при ступенчатом сигнале на входе

c_вых(t) = F(t) = (1 – е^-t/ ); (3.7)

– при импульсном сигнале на входе

. (3.8)

Графическая интерпретация аналитических выражений для F(t) и (t) показана на рис. 3.4 и 3.5.

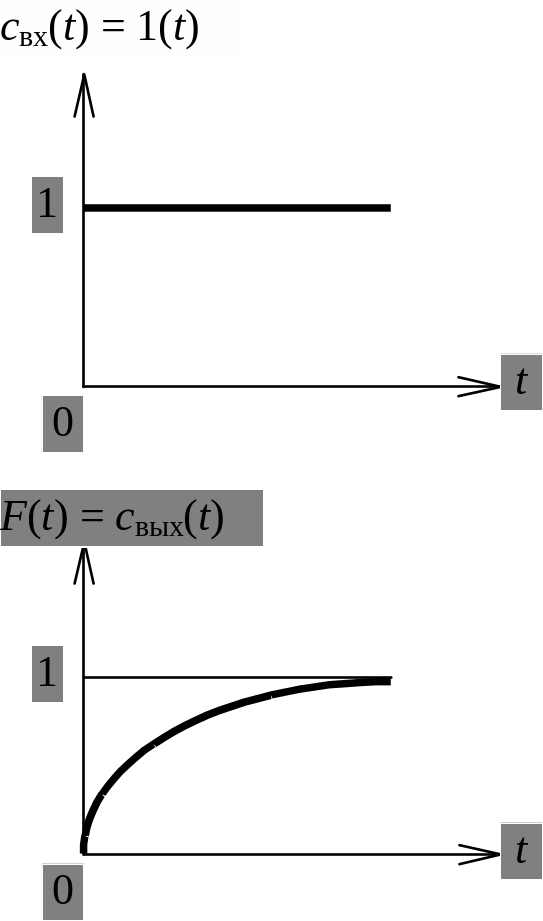
Рис. 3.4. F-кривая МИС Рис. 3.5. -кривая МИС

Наилучшим образом МИС соответствует реальным потокам в проточных аппаратах c мешалкой (рис. 3.3), высота которых мало отличается от диаметра d, мешалка создает высокую степень перемешивания, а объемная скорость потока v невелика.