Алгоритм симплекс-метода

1. Записываем задачу линейного программирования в канонической форме, составляем первую симплекс-таблицу и находим начальный опорный план.

2. Найденный опорный план исследуем на оптимальность, проверяя f-строку:

а) если в f-строке нет отрицательных элементов, то план оптимален и можно по таблице описать решение. Если при этом нет и нулевых элементов, то оптимальный план единственен; если же есть хотя бы один нулевой, то оптимальных планов бесконечно много;

б) если в f-строке есть хотя бы один отрицательный элемент, которому соответствует столбец неположительных элементов, то целевая функция не имеет максимума, т. е. ;

в) если в f-строке есть хотя бы один отрицательный элемент, а в его столбце есть хотя бы один положительный, то опорный план не является оптимальным и переходим к пункту 3.

3. Переход к новому опорному плану осуществляется в следующем порядке:

а ) из отрицательных элементов f-строки выберем наибольший по модулю пусть это , назовем соответствующий ему столбец с номером s разрешающим и будем помечать ;

б ) в разрешающем столбце выберем положительный элемент по минимальному отношению свободных членов к соответствующим положительным коэффициентам разрешающего столбца . Пусть . Положительный элемент разрешающего столбца, на котором достигается минимум называется разрешающим элементом, будем помечать его квадратиком, соответствующую строку с номером r , будем называть разрешающей строкой и помечать ;

в) переменные и , отвечающие разрешающей строке и разрешающему столбцу меняем местами;

г) разрешающий элемент заменяем ему обратным ;

д) остальные элементы разрешающей строки делим на ;

е) остальные элементы разрешающего столбца делим на ;

ж) элементы, не принадлежащие разрешающей строке и разрешающему столбцу, вычисляем по правилу «прямоугольника»:

, где – пересчитанный элемент.

Э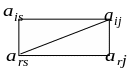 лементы, входящие в эту формулу, расположены в вершинах воображаемого прямоугольника, элемент ,который нужно пересчитать и разрешающий элемент лежат на диагонали этого прямоугольника.

Эта диагональ называется главной, тогда пересчитанный элемент равен разности произведений элементов главной и побочной диагоналей, деленной на разрешающий элемент.

4. Переходим к пункту 2.

Очевидно, процесс заканчивается, когда f-строка последней таблицы (не считая свободного члена) не содержит отрицательных элементов. Последний столбец последней таблицы дает ответ: оптимальный план и оптимальное значение целевой функции.

Замечание. При переходе к следующей таблице рекомендуется вначале найти f–строку: если она не содержит отрицательных элементов, то нужно лишь найти последний столбец (ответ).

Напомним, что задача на вычисление минимума приводится к задаче на вычисление максимума заменой f на (–f), при этом

.

Каноническая задача линейного программирования может иметь не совсем специальный вид, когда свободные члены каких- либо уравнений системы ограничений (1.3.5) отрицательны. В этом случае нужно найти допустимый первоначальный опорный план, а затем начать алгоритм симплекс-метода.