1.3. Симплекс-метод

1.3.1. Идея симплекс-метода

Как уже указывалось, реальные задачи линейного программирования содержат, как правило, большое число ограничений и неизвестных. К числу общих универсальных методов, позволяющих найти решение любой задачи линейного программирования относится прежде всего так называемый симплекс-метод или метод последовательного улучшения плана.

С самого начала отметим, что симплекс-метод предназначен для решения канонической задачи линейного программирования (п. 1.1.3). Итак, рассмотрим задачу линейного программирования с ограничениями в виде уравнений:

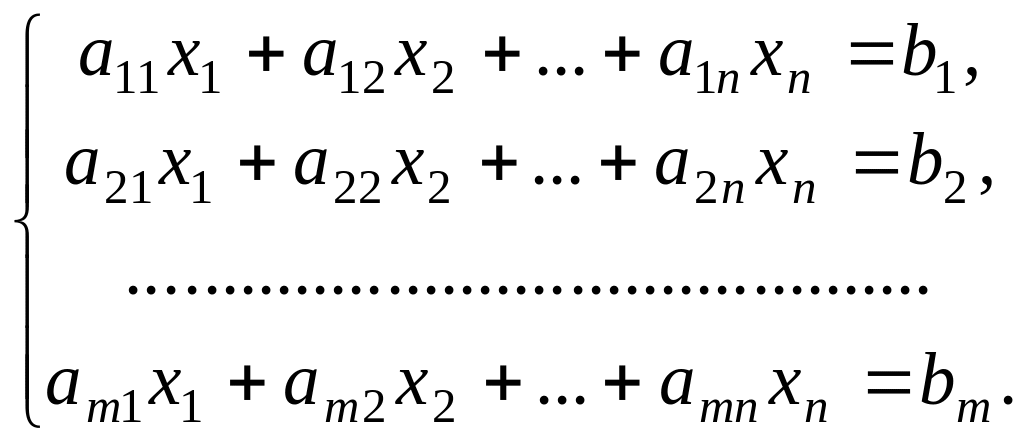(1.3.1)

Среди неотрицательных решений системы уравнений (1.3.1) нужно найти такое, которое максимизирует функцию f. Для начала работы по симплекс-методу требуется, чтобы заданная система уравнений была приведена к виду, когда какие-то из неизвестных выражены через остальные неизвестные, причем свободные члены этих выражений неотрицательны.

Неизвестные системы, которые выражены через остальные, называются базисными. Остальные неизвестные называются свободными.

Д

(ограничение по ресурсу ),

(ограничение по ресурсу

ля примера рассмотрим задачу об оптимальном использовании ресурсов, которую мы решали ранее (см. п. 1.2).

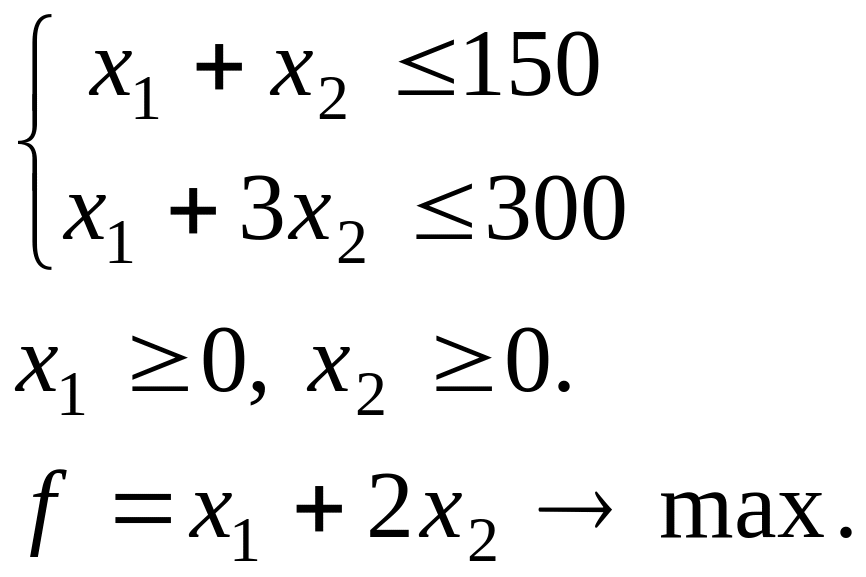
Приведем ее к каноническому виду, вводя дополнительные неотрицательные переменные .

(1.3.2)

Заметим, что переменные несут определенный экономический смысл, они определяют остатки ресурсов и соответственно. Полученную систему уравнений (1.3.2) можно легко разрешить относительно переменных .

Таким образом, переменные – базисные, а – свободные. Придавая свободным переменным произвольные значения, будем получать значения базисных переменных .

Пусть тогда .

Решение системы соответствующее нулевым значениям свободных переменных, называется базисным решением.

В нашем примере (0; 0; 150; 300) – базисное решение.

Очевидно, разрешив систему (1.3.2) относительно другого набора свободных и базисных переменных, получим другое базисное решение. Например, разрешив систему (1.3.2) относительно базисных переменных : и придавая свободным переменным и нулевые значения, получим второе базисное решение – (300; 0; –150; 0).

Обратим внимание, что второе базисное решение не удовлетворяет условию неотрицательности.

Базисное решение, удовлетворяющее условию неотрицательности называется опорным планом.

В нашем примере первое базисное решение (0; 0; 150; 300) является опорным планом, а второе базисное решение (300; 0; –150; 0) не является опорным планом. Важность понятия опорного решения определяет следующая основная теорема линейного программирования. Если каноническая задача линейного программирования разрешима, то её оптимальный план содержится среди конечного числа её опорных планов.

Из этой теоремы следует, что оптимальное решение канонической задачи линейного программирования может быть найдено путем перебора ее опорных планов, число которых конечно. Теоретически возможен такой подход к решению задачи линейного программирования: найти все опорные планы и выбрать из них оптимальный, т. е. тот, на котором f максимальна.

Идея симплекс-метода состоит в отказе от простого перебора и состоит из следующих этапов:

1. построение начального опорного плана;

2. проверка опорного плана на оптимальность;

3. если опорный план не является оптимальным, то переходим к новому опорному плану, на котором значение целевой функции f больше, чем на предыдущем плане.

После нескольких шагов достигается оптимальный опорный план.

Рассмотрим реализацию идеи симплекс-метода на примере задачи об оптимальном использовании ресурсов.

Ранее мы получили опорный план (0; 0; 150; 300), он соответствует системе (1.3.3)

значение целевой функции на этом плане . В этом плане переменные принимают минимально возможные значения равные нулю. Легко понять, что этот опорный план не оптимален, т. к. можно увеличить за счет увеличения любой из свободных переменных . Это связано с тем, что коэффициенты при и в записи f положительны. При этом более выгодно увеличивать , т. к. коэффициент при в записи f больше, чем при . Не меняя значении будем увеличивать до максимально возможного значения.

Из условия неотрицательности и , учитывая что , получаем:

Откуда с учетом неотрицательности . Следовательно . При переменная окажется равной нулю, а = 150 –100 = 50. Таким образом, мы получили новый опорный план , который соответствует системе, в которой базисные переменные выражены через свободные – . Чтобы записать систему в новых базисных переменных из второго уравнения системы (1.3.3) выразим и подставим полученное для выражение в первое уравнение:

откуда

(1.3.4)

П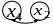 ереход от системы (1.3.3) к новой системе (1.3.4) будем кратко описывать так: мы ввели в базис переменную и вывели из базиса переменную , т. е. поменяли местами с в наборе базисных и наборе свободных переменных, и обозначать . Заметим,

что при этом , что больше чем значение , т. е. новый опорный план лучше предыдущего. Чтобы узнать является ли новый опорный план оптимальным нужно выразить через новые свободные переменные ,

откуда .

Из формулы для видно, что значение можно увеличивать только за счет увеличения , так как при увеличении целевая функция будет уменьшаться, т. к. переменная входит в выражение для с отрицательным коэффициентом.

Определим границу роста переменной , сохраняющую неотрицательности переменных и , при этом как свободная переменная:

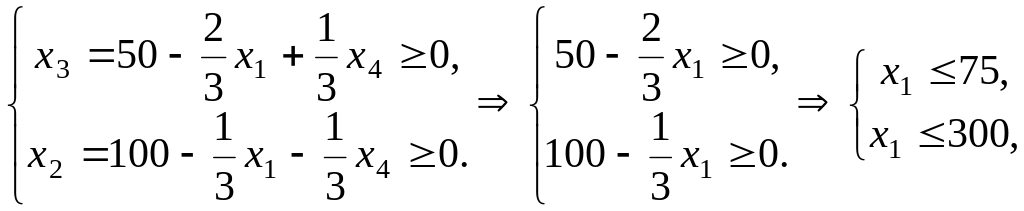
следовательно, диапазон изменения переменной определяется неравенством , а её максимально возможное значение . При переменная , а .

Таким образом, вводим в базис, а выводим из базиса и получаем следующий опорный план Чтобы проверить его на оптимальность нужно определить знаки коэффициентов при свободных переменных в записи , предварительно разрешив систему (1.3.4) относительно базисных переменных и :

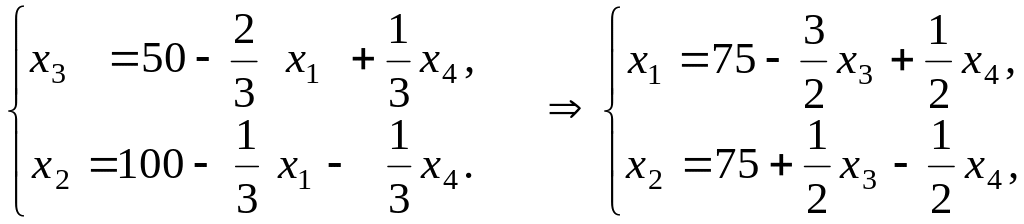
откуда

. Так как в записи целевой функции все коэффициенты при свободных переменных отрицательны, то дальнейшее улучшение f невозможно. То есть план является оптимальным и .