1. Основные методы решения задач линейного программирования

1.1. Введение в линейное программирование

1.1.1. Общая задача оптимизации

В условиях рыночной экономики управление и планирование является наиболее сложными функциями в работе отдельного предприятия, отрасли, народного хозяйства в целом. Решение современных экономических задач невозможно без использования математического аппарата. Поэтому роль математических методов в экономике постоянно возрастает, а современный уровень компьютеризации предоставляет большие возможности для развития и совершенствования этих методов.

Большое число планово-экономических задач и задач управления связано с распределением каких-либо, как правило, ограниченных ресурсов (сырья, рабочей силы, электроэнергии и т. д.). Необходимо определить, как использовать имеющиеся в распоряжении ресурсы, чтобы получить наилучший экономический эффект. В действительности, в самых различных областях нашей жизнедеятельности мы постоянно сталкиваемся с аналогичными задачами. Нам известна ситуация, в которой мы находимся, и множество возможных альтернативных вариантов нашего дальнейшего поведения. Естественно стремление из всех допустимых вариантов выбрать наилучший, или, как принято говорить, оптимальный вариант. Математически это обычно сводится к нахождению наибольшего или наименьшего значения некоторой функции f(x), определяющей цель поставленной задачи, при условии, что аргумент x пробегает некоторое данное множество X. Пишут так:

(1.1)

Определенная таким образом задача (1) называется задачей оптимизации. Множество X называется областью допустимых планов (ОДП) данной задачи, а функция – целевой функцией.

В подавляющем большинстве случаев, т. е. а множество задается системой ограничений:

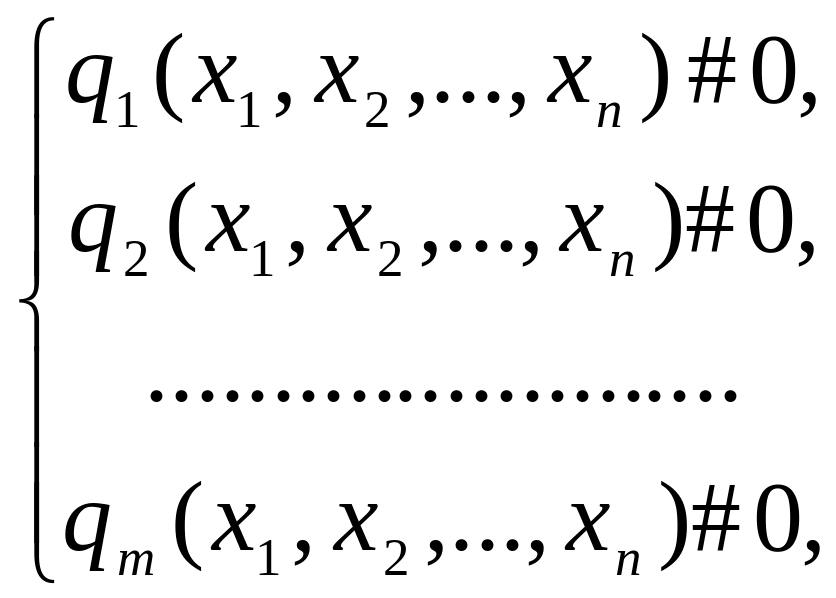(1.2)

где # обозначает один из знаков списка , – заданные функции n переменных Иначе говоря, область допустимых планов есть множество точек , удовлетворяющих системе (1.2). Требуется найти при условии (1.2).

Точка или точки, если их несколько, в которых достигается оптимальное значение, называются оптимальными решениями или оптимальными планами.

Совокупность методов, позволяющих решать указанные задачи, называется математическим программированием. В зависимости от вида целевой функции и ограничений математическое программирование делится на линейное и нелинейное. Наиболее простой и часто встречающийся случай, когда функции являются линейными. Тогда говорят о задаче линейного программирования (ЛП).

1.1.2. Задачи линейного программирования

Подсчитано, что в настоящее время 80 – 85% всех решаемых на практике задач оптимизации относятся к задачам линейного программирования.

Линейное программирование (ЛП) оформилось как отдельный раздел прикладной математики в 30 – 40 годах ХХ века, когда выяснилось, что целый ряд задач из сферы планирования и управления может быть сформулирован в виде задач ЛП. В работе российского ученого, лауреата Государственной, Ленинской и Нобелевской премий академика Леонида Васильевича Канторовича «Математические методы организации и планирования производства» (1939) впервые была сформулирована задача линейного программирования, описывающая реальную экономическую ситуацию, и разработан алгоритм ее решения. Позднее американский ученый Джон Данциг описал один из эффективных методов решения задач линейного программирования, так называемый симплекс-метод.

Рассмотрим несколько примеров задач линейного программирования.

1. Задача о рационе. Суточный рацион состоит из двух продуктов П₁ и П_2, причем продукт П₂ можно включить в рацион в количестве не более 200 ед. Цены на продукты П₁ и П₂ соответственно равны 20 и 40 д.е. Содержание питательных веществ А и В в продуктах и минимальные нормы потребления этих веществ указаны в табл.1.1.

Определить оптимальный рацион, удовлетворяющий потребности организма в питательных веществах, и требующий наименьших затрат.

Таблица 1.1

Задача о рационе

Содержание питат. веществ в 1 ед. продукта	А	В
П1 П2	0,2 0,2	0,4 0,2
Мин. норма потребления питат. веществ	120	160

Построим математическую модель этой задачи.

Пусть – количества продуктов П₁ и П₂ соответственно, обеспечивающие искомый суточный рацион. По смыслу задачи неотрицательны. Общее количество вещества А в обоих продуктах равно Оно должно быть не менее 120, т. е. Аналогичное неравенство получаем для вещества В:

С учетом того, что продукт П₂ можно включить в рацион в количестве не более 200 ед., получаем систему ограничений данной задачи:

Цель задачи – минимизировать затраты

Очевидно, общая стоимость суточного рациона

Заметим, что к подобной схеме могут быть сведены задачи определения состава сплавов, смесей, смесей минеральных удобрений, состава услуг на предприятиях сервиса и т. д.

2. Задача о банке. Собственные средства банка в сумме с депозитами составляют не более 100 млн долл. Часть этих средств, не менее 35 млн долл. должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, т. к. в случае необходимости обратить кредиты в деньги без существенных потерь невозможно. Ценные бумаги являются ликвидными активами, их можно в любой момент продать, получив прибыль или без большого убытка. Поэтому банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги. В нашем примере ценные бумаги должны составлять не менее 30% средств банка. Доходности кредитов и ценных бумаг соответственно равны с₁ и с₂. Так как кредиты менее ликвидны, чем ценные бумаги, то обычно с₁ > с₂.

Пусть – средства (млн долл.), размещенные в кредитах, – средства, вложенные в ценные бумаги. По смыслу задачи неотрицательны.

И

(балансовое ограничение),

(кредитное ограничение),

(ликвидное ограничение),

меем следующую систему линейных ограничений:

(1.3)

Цель банка состоит в том, чтобы получить максимальную прибыль:

. (1.4)

Мы получим задачу ЛП с ограничениями (1.3) и целевой функцией (1.4).

2. Задача об оптимальном использовании ресурсов. Имеется видов ресурсов , которые используются для производства видов продукции . Пусть – количество единиц ресурса , необходимое для производства одной единицы продукции Допустим, что запасы ресурса равны 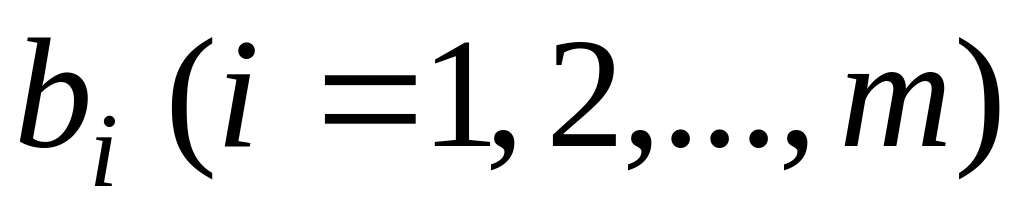, а прибыль от реализации одной единицы продукции составляет Требуется при данных ресурсах определить план производства, то есть определить сколько продукции каждого вида нужно произвести, чтобы суммарная прибыль от реализации продукции была максимальной. Внесем условия задачи в таблицу (табл. 1.2).

Таблица 1.2

Задача о ресурсах

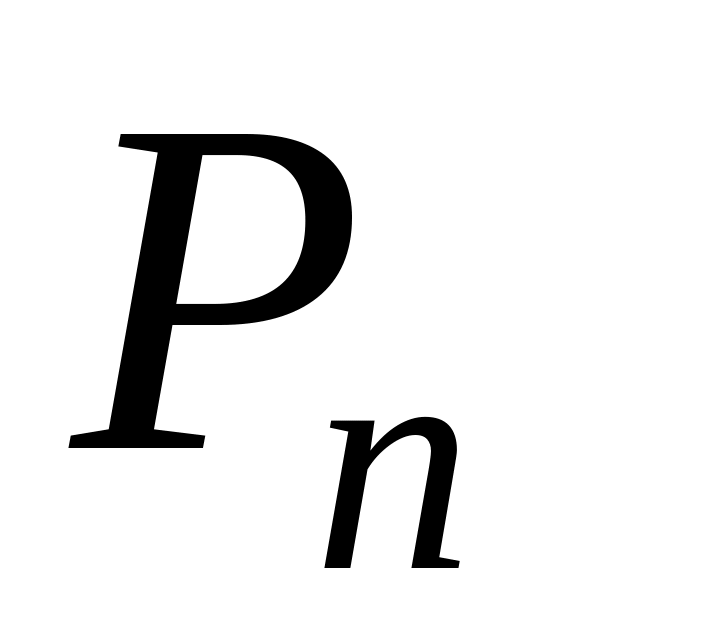
Виды ресурсов	Виды продукции … …	Запасы ресурсов
… …	. . . . . . … . . . . . . … . . . . . .	. . . . . .
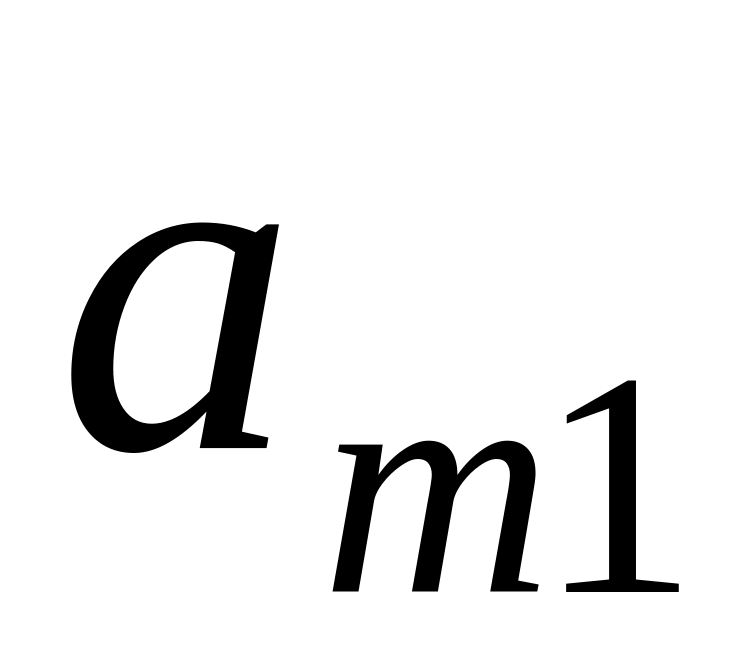Прибыль	. . . . . .

Построим математическую модель этой задачи. Обозначим – план производства, где – количество единиц продукции предусмотренное планом Для производства единицы продукции нужно единиц ресурса для производства единиц нужно – единиц . . .; для единиц нужно единиц . Так как при плане расход не должен превосходить его запас, то

Аналогично определяются ограничения по каждому виду ресурсов. Для

………… . . . . . . . . . . . . . . . . . . . . . . .

Для

Кроме того, все При реализации единицы продукции прибыль составит ; единиц продукции – и т. д. Суммарная прибыль

Таким образом, получим систему линейных ограничений:

условия неотрицательности:

линейную целевую функцию:

Уже на основании трех рассмотренных примеров можно указать основные этапы построения математической модели задачи линейного программирования:

• ввести обозначения переменных, т. е. величины которые характеризуют экономический процесс;

• исходя из цели исследования, составить целевую функцию, экстремум которой нужно найти, т. е.

• составить систему ограничений, которым удовлетворяют переменные учитывая экономические показатели задачи и их количественные закономерности.

Дадим теперь общую формулировку задачи линейного программирования.

Пусть S – система линейных ограничений, состоящая из линейных уравнений и нестрогих линейных неравенств с n переменными Без ограничения общности можно считать, что все неравенства системы S имеют вид , т. к. любое неравенство вида равносильно неравенству Обычно система S включает в себя условие неотрицательности всех переменных: . Имеется линейная целевая функция вида

Требуется найти удовлетворяющее S, на котором целевая функция принимает максимальное значение:

З аметим, что задача на вычисление минимума приводится к задаче на вычисление максимума заменой на при этом Поясним это графически на примере функции одной переменной (рис. 1.1):