7.3. Расчет временных параметров сетевого графика

7.3.1. Расчет параметров событий

К основным показателям сетевого графика, позволяющим определить критический путь и его продолжительность, относятся ранний и поздний сроки свершения события, резерв времени события.

Расчетные формулы указаны в табл. 7.3.

Таблица 7.3

Основные показатели сетевого графика

Элемент сети	Параметр	Формула
Событие i.	– ранний срок свершения события i – величина пути максимальной продолжительности от исходного события сети до события i	(7.1) , k – номер предшествующего события(их может быть несколько)
	– поздний срок свершения события i – величина пути минимальной продолжительности, ведущего от завершающего события сети до события i	(7.2) , j – номер последующего события (j – может быть несколько)
	– резерв времени наступления события i – величина допустимого периода времени, на которое можно задержать наступление события i, не вызывая увеличения срока выполнения всего проекта	(7.3)

Учитывая введенное в п.7.1 определение критического пути и введенные формулы (7.1–7.3), можно записать алгоритм нахождения критического пути.

1. Полагая найти по формуле 7.1) для

2. Полагая «обратным ходом» найти по формуле (7.2) для

3. Найти по формуле 7.3) для

4. Найти критический путь, как последовательность событий, для которых (критические события не имеют резервов времени). Найти

Пример. Найти критический путь и для сетевого графика, изображенного на рис. 7.4 по данным табл.7.1.

Решение. Результаты вычисления по указанному выше алгоритму запишем в табл. 7.4, используя данные по табл. 7.2.

Вычисления. 1. Заполняем столбец сверху вниз:

и т. д.

2. Заполняем столбец снизу вверх:

и т. д.

3. Заполним столбец по формуле

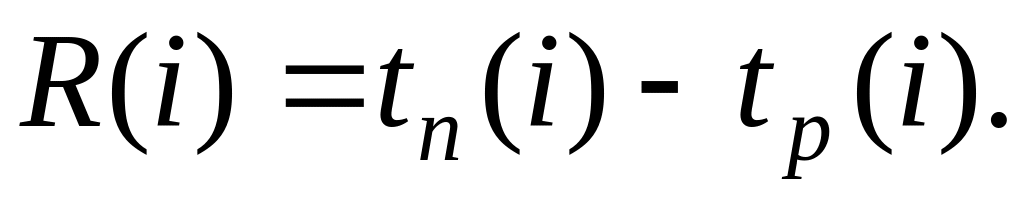
4. Критический путь

Замечание. При небольшом числе вершин вычисление величин t_p(i), t_п(i), и поиск критического пути удобно проводить непосредственно на сетевом графике. Для этого при построении чистового варианта сетевого графика каждый из кружков, изображающих вершины, делится на четыре сектора (рис. 7.5).

Таблица 7.4.

Расчет временных параметров событий

Событие i
1	0	0	0
2	13	13	0
3	30	30	0
4	50	50	0
5	55	55	0
6	61	64	3
7	69	69	0
8	74	74	0
9	85	85	0

Верхние секторы указывают номера вершин. Перемещаясь по сетевому графику слева направо от S к F, последовательно вычисляют и записывают результаты в левые секторы. Полагая и перемещаясь, справа налево от F к S, последовательно вычисляют и записывают результаты в правые секторы. Затем нижние секторы заполняются по формуле (7.3).

Дуги, лежащие на критическом пути выделены жирными линиями.