6.3.2. Поиск кратчайшего гамильтонова цикла

Задача. Имеется n пунктов, соединенных между собой дорогами так, что из любого пункта можно проехать в любой другой пункт. Известно время переезда из пункта i в пункт j. Требуется найти путь минимальной длины, начинающийся и заканчивающийся в определенном пункте и проходящий через все пункты. В теории графов эта задача известна как «задача коммивояжера» (торговец, выехавший из определенного пункта с образцами товаров должен побывать в каждом городе один раз и вернуться назад).

Таблица 6.2

Матрица расстояний

J i	V1	V2	V3	V4	V5
V1	0	30	40	15	6
V2	10	0	18	7	9
V3	20	30	0	1	10
V4	25	10	35	0	5
V5	9	8	7	6	0

Перейдем на язык графов: вершины графа – пункты, дуги – дороги, длина дуги ( не обязательно равно и Очевидно, что искомый путь – это гамильтонов цикл наименьшей длины (см. определение).

Алгоритмы решения этой задачи изложены в различной литературе по теории графов [1], [17].

Пусть n = 5. Орграф на рис. 6.10 задан матрицей расстояний (табл. 6.2).

О

если переезд совершается из в ;

если переезд не совершается из в .

тметим, что если , то это означает, что дуги нет. Составим математическую модель задачи. Введем переменные такие, что для них

При этом для всех Тогда найти искомый гамильтонов цикл означает найти матрицу такую что целевая функция имела бы минимальное значение.

(1)

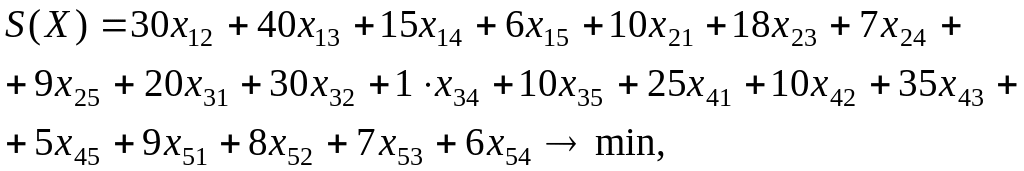
и выполнялась система ограничений

	для всех i; (сумма элементов каждой строки равна 1);
	для всех j; (сумма элементов каждого столбца равна 1);
	целые для всех i, j;
	( – только 0 или 1).

Очевидно, что уравнения системы (2) обеспечивают выполнение условия, что из каждого пункта выезжают только один раз и только в одном направлении.

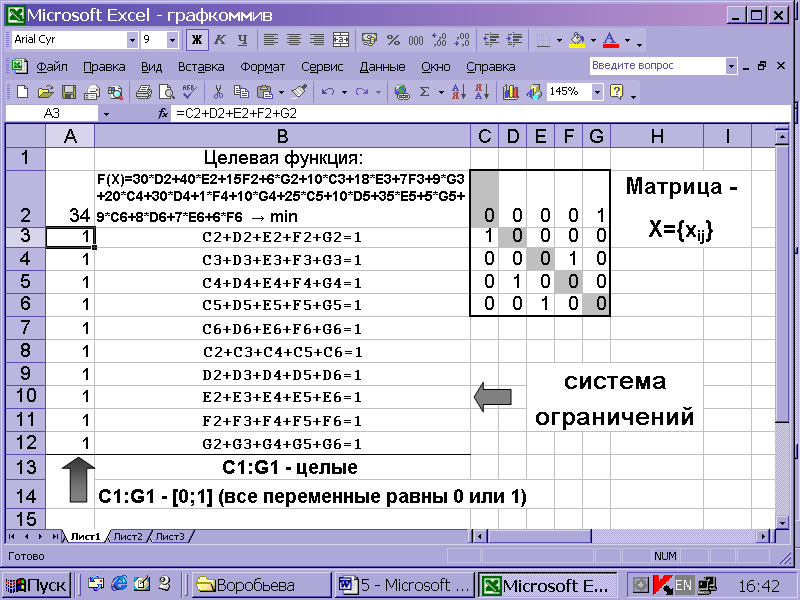
Решим задачу в приложении Excel с помощью надстройки Поиск решения (подробно решение подобной задачи рассматривается в п. 8). На рис. 6.11 представлен вид экрана при решении задачи.

Пояснения к решению задачи на компьютере:

1. В ячейку А2 вводится формула для расчета целевой функции; в А3:А12 – левые части соответствующих ограничений. Начальные значения всех элементов матрицы Х равны 0, т.е. в ячейки С2:G6 вводят 0.

2. В диалоге Добавление ограничений следует ввести дополнительные ограничения: все x_ij – целые, т. е. выделить диапазон C2:G6 и указать – целые.

3. На вопрос Изменяя ячейки указать (т. е. выделить) все ячейки матрицы Х, кроме диагональных, так как они должны остаться равными 0 (диагональные элементы на рисунке выделены серым фоном).

В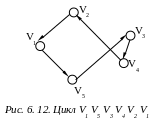 результате получена матрица

Этой матрице соответствует

т. е. гамильтонов цикл минимальной длины найден (рис. 6.12).

Отметим, что введенные понятия и примеры в п. 6 носят ознакомительный характер и являются вводными для следующего раздела. Для получения более детальной информации по теории графов следует обратиться к специальной литературе, например, [17].