2.6. Открытая модель транспортной задачи

В открытой (несбалансированной) транспортной задаче суммарные запасы не совпадают с суммарным спросом, т. е.

.

При этом возможны два случая.

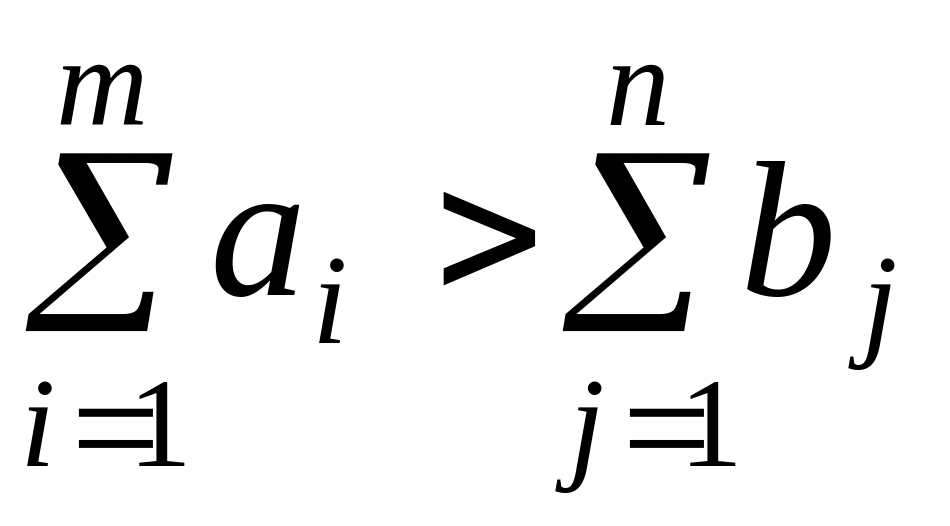1. Если , то объем запасов превышает объем потребления, спрос всех потребителей будет удовлетворен полностью и часть запасов останется невывезенной. Для решения задачи вводят фиктивного 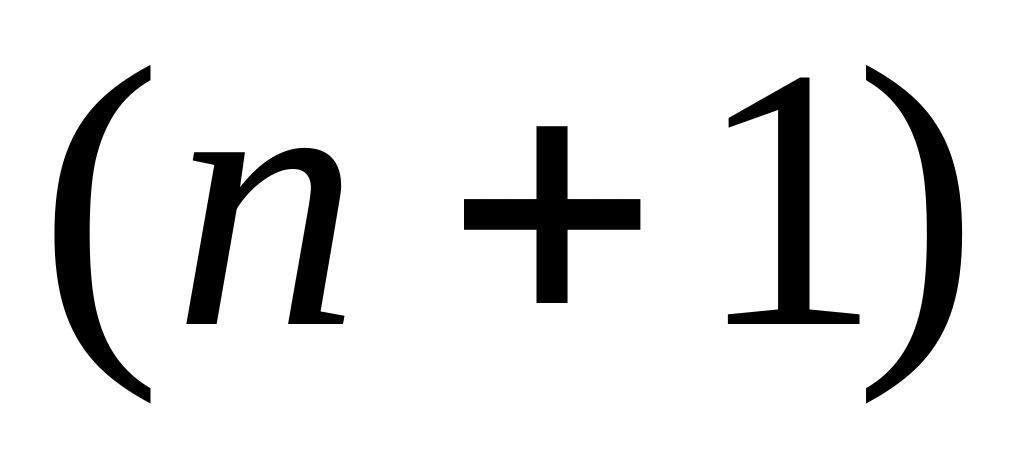– потребителя, потребности которого 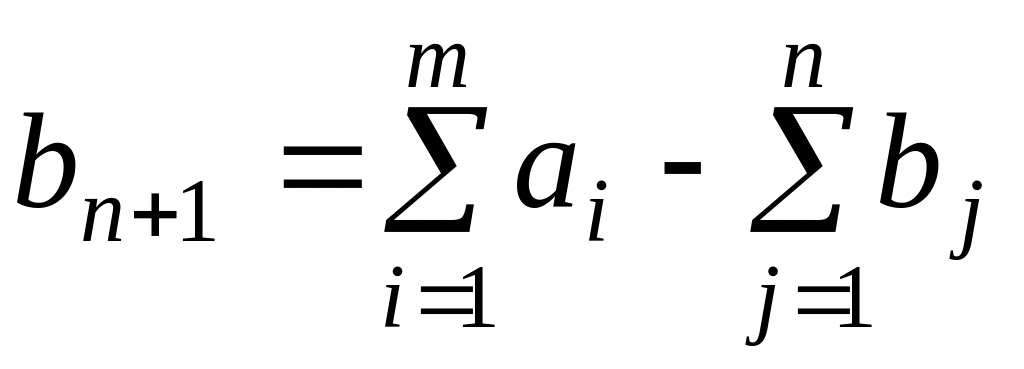, а тарифы этого потребителя 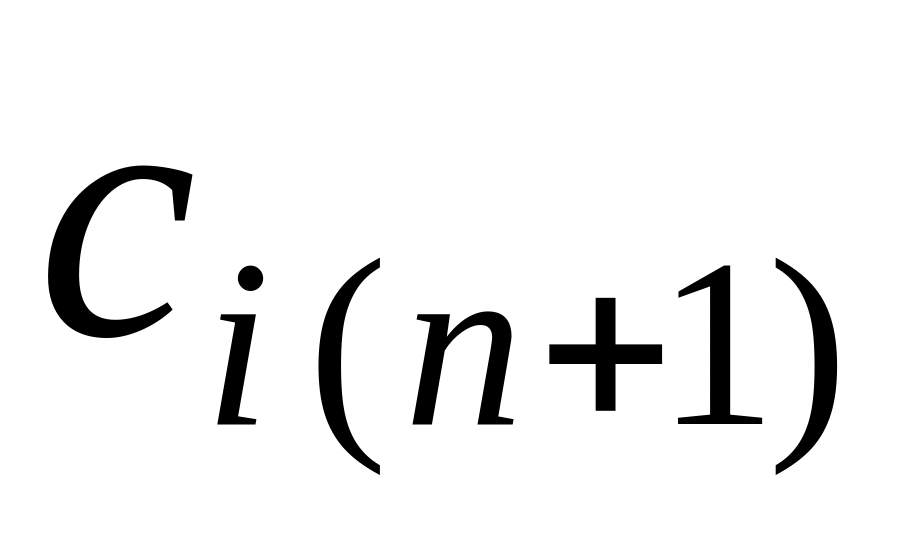, где 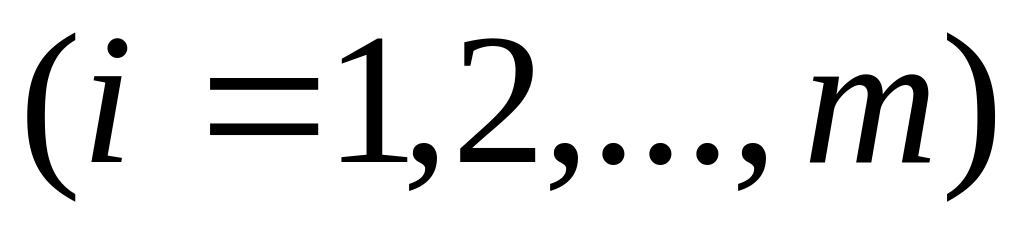полагают равными нулю, чтобы они не влияли на транспортные расходы.

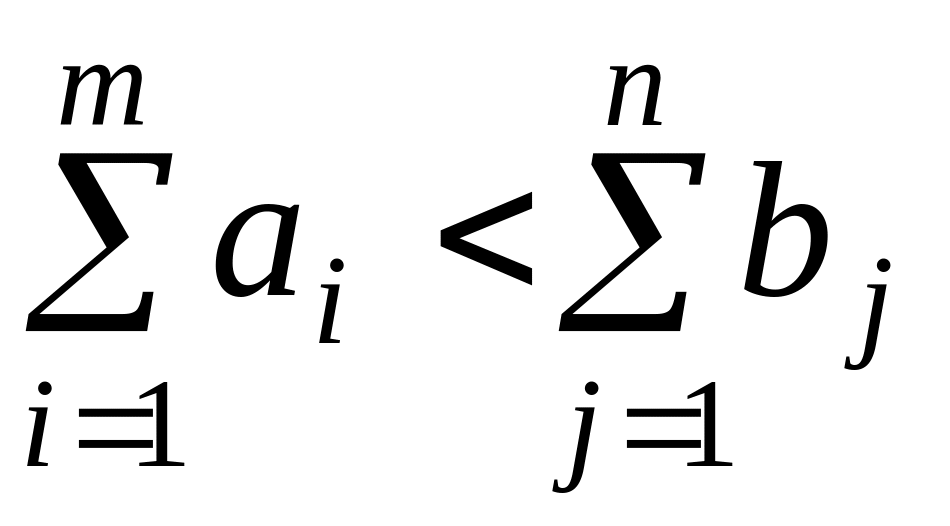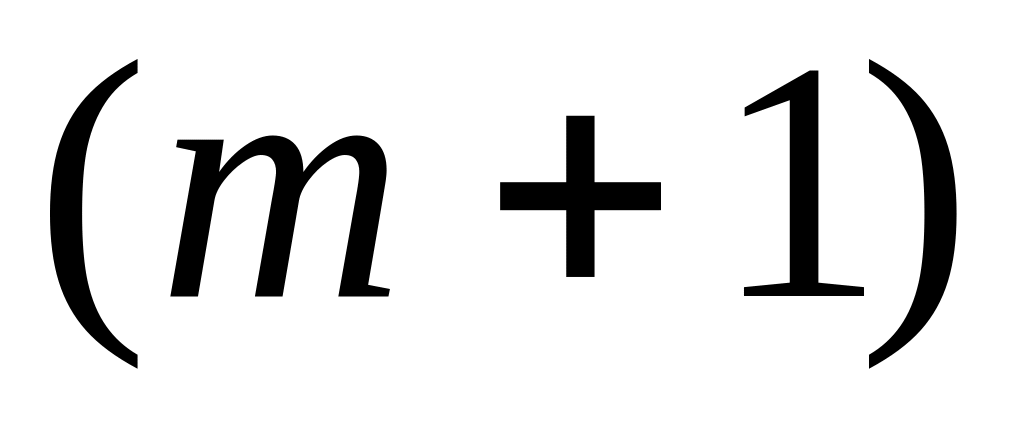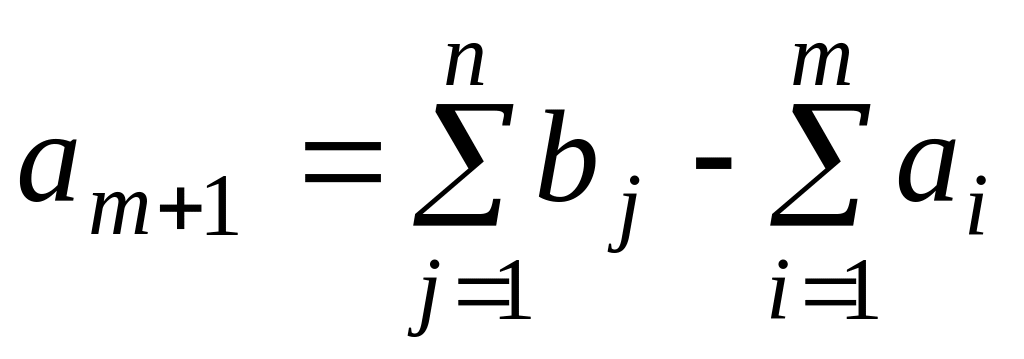2. Если , то объем потребления превышает объем запасов. В этом случае вводим фиктивного – поставщика, запасы которого , а тарифы 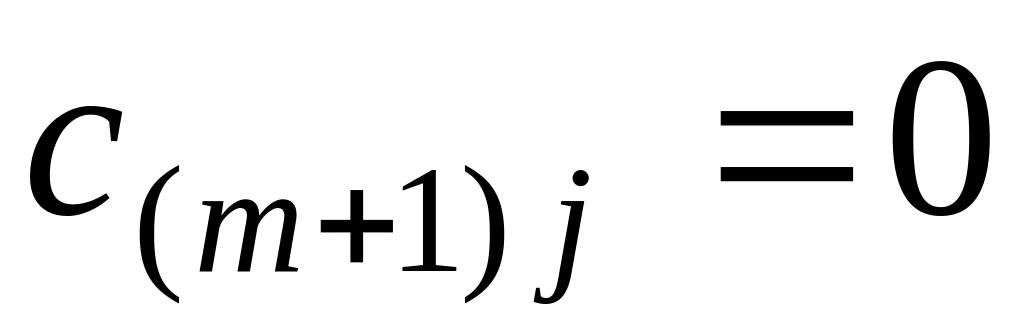, где .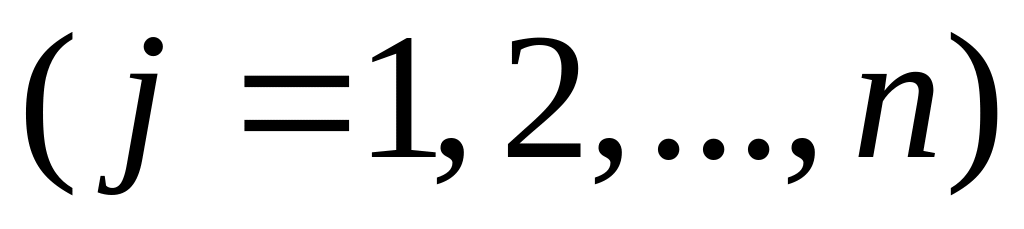

Таким образом, открытая транспортная задача решается сведением ее к закрытой транспортной задаче.

2.7. Приложение транспортной задачи к решению некоторых экономических задач

Алгоритм решения транспортной задачи может быть использован при решении некоторых экономических задач, не имеющих ничего общего с транспортировкой груза. В этом случае тарифы имеют различный смысл в зависимости от конкретной экономической задачи. К ним относятся следующие задачи:

• оптимальное закрепление за станками операций по обработке деталей;

• увеличение производительности автомобильного транспорта за счет минимизации порожнего пробега и др.

Рассмотрим конкретную задачу о выборе оптимального варианта использования производственного оборудования.

Пример 4. На трикотажной фабрике имеется три группы станков, каждая из которых может выполнять пять операций по обработке изделий (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков соответственно равно 100, 250 и 180 часов. Каждая из операций должна выполняться соответственно 100, 120, 70, 110 и 130 часов.

Определить сколько времени и на какую операцию нужно использовать каждую группу станков, чтобы обработать максимальное количество изделий.

Производительности каждой группы станков на каждую операцию заданы матрицей :

.

Решение. Пусть – время, в течение которого используется i–я группа станков для выполнения j–й операции. Воспользуемся алгоритмом решения закрытой транспортной задачи, т. к.

(ч).

В этой задаче нужно найти максимум целевой функции , поэтому тарифы возьмем со знаком минус, тогда . Напомним, что .

Составим первоначальный опорный план методом наименьших затрат и проверим его на оптимальность методом потенциалов (табл. 2.12).

Таблица 2.12

Первоначальный опорный план

	–5	–10	–15	–9	–7	Запасы
2	–3 40	–5	–11	–7> –10 +	5 60 –	100
0	–5 60	–10 120	–15 70	–3	–2	250
–3	–4	–8	–6	–12 110 –	–10 70 +	180
Потребности	100	120	70	110	130	530 530

В клетке (1,4) нарушено условие оптимальности. Составим для этой клетки цикл и, перемещаясь по этому циклу , получаем новый опорный план, который является оптимальным (табл. 2. 13).

Итак ; (шт).

Таблица 2.13

Оптимальный план

	–5	–10	–15	–12	–10
2	–3 40	–5	–11	–10 60	–5
0	–5 60	–10 120	–15 70	–2	–2
0	–4	–8	–6	–12 50	–10 130

Таким образом, на первой группе станков целесообразно выполнять первую и четвертую операции в течение 40 и 60 часов соответственно; на второй группе – первую, вторую и третью операции продолжительностью 60, 120 и 70 часов соответственно; на третьей группе станков – четвертую и пятую операции продолжительностью 50 и 130 ч соответственно. При этом максимальное количество обработанных изделий составит 5170 штук.

Транспортная задача – одна из распространенных задач линейного программирования. Её цель – разработка наиболее рациональных путей и способов транспортировки товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время передвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами и услугами и т. д.