
- •Основы моделлогии
- •Основные понятия моделлогии.
- •Примеры применения введённых понятий
- •Введение
- •2.2. Моделирование трансформатора
- •2.1 Введение
- •2.2. Моделирование горизонтальной ветви модели трансформатора в частотной области.
- •2.3. Моделирование вертикальной ветви модели трансформатора в частотной области.
- •2.4. Моделирование хх во временной области для испытанных ранее тн.
- •2.5. Моделирование кз во временной области для испытанных ранее тн. Литература
Основы моделлогии
Основные понятия моделлогии.
Моделирование в широком смысле – это исследование каких-либо явлений, процессов или систем объектов путём построения и изучения их моделей [1].
Ниже приводится классификация типов моделирования. Основное внимание уделяется моделированию устройств, при котором находятся значения каких-либо физических величин. Поэтому моделирование оказывается аналогичным измерению.
Как известно, измерение – это процесс получения значения физической величины опытным путём с помощью специальных технических средств []. За рубежом получило распространение более, на наш взгляд правильное определение: Измерение – это процесс получения значений параметров модели опытным путём с помощью специальных технических средств. Тогда моделирование устройств, используемых при измерении, можно определить как процесс получения значений параметров модели расчётным путём. С понятиями «Измерение» и «Моделирование» тесно связано ещё одно понятие – Контроль- процесс наблюдения и проверки процесса функционирования и фактического состояния управляемого объекта [Википедия]. Отличие понятий «Контроль» и «Измерение» состоит в том, что значение параметра объекта при измерении фиксируется и определяется его неопределённость (доверительный интервал с заданной вероятностью), в то время как при контроле это может не делаться, но обязательно осуществляется сравнение фактического значения параметра с желаемым. Если при этом реализуется воздействие на объект с целью приведения значений параметров к желательному уровню, то такой процесс называется управлением. При управлении значения параметров могут не фиксироваться, и результат сопоставления сравнения истинного значения параметра с желаемым может также не быть доступным наблюдателем. Все приведённые понятия близки, а часто не различимы. Перед измерением принимается модель объекта (по результатам измерения она может корректироваться). Определяется измерение параметров этой модели –«идентификация объекта». Оценка неопределённости осуществляется с помощью той или иной модели погрешности (с Р=1, Р=0,95 и т.д.). Результат измерения может сравниваться с желаемым, допустимым, эталоном и т.д. и делается вывод о пригодности объекта (контроль), вводится корректирующее воздействие (моделирование).
Приведённая ниже классификация является открытой системой, т.к. может быть неограниченно расширена путём введения новых классификационных признаков
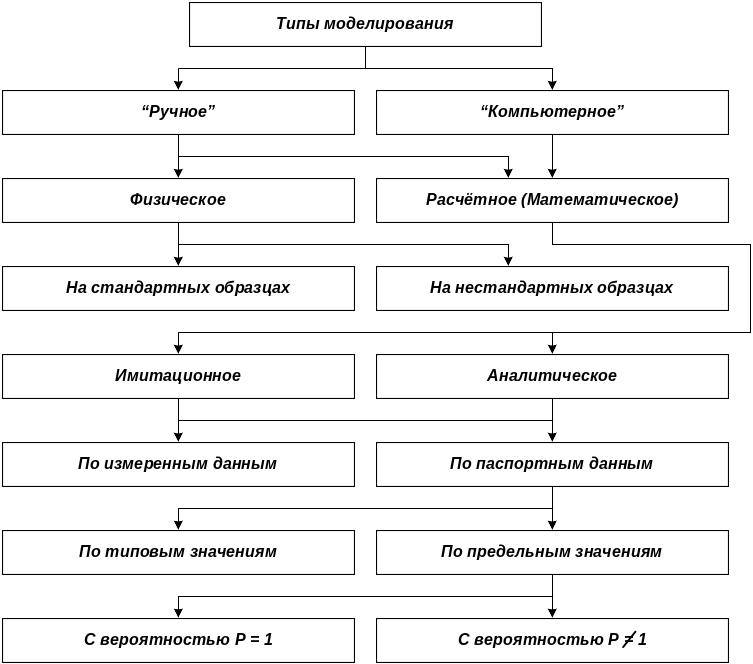
Рис. 1. Классификация типов моделирования
При "ручном" (немашинном) моделирование вычислительные устройства могут применяться, но их влияние на точность и скорость расчётов несущественно. Модели для ручного и машинного моделирования могут существенно различаться. На практике, немашинное проектирование обычно проще, но менее точное и предшествует компьютерному. Совпадение результатов немашинного и машинного проектирования в некоторых характерных точках является одним из признаков адекватности моделирования (смотри ниже).
Физическое моделирование ("макетирование") предполагает использование макетов объектов и непрерывно вытесняется компьютерным моделированием. Макеты могут изготавливаться под каждый новый объект, но могут использоваться и стандартизованные макеты (evaluation boards).
Расчётное (математическое) моделирование делится на имитационное моделирование (воспроизводит функционирование объекта во времени), и аналитическое моделирование (называемое также математическим, функциональным). При аналитическом моделировании выходные переменные объекта связаны с входными посредством математических уравнений. В литературе на английском языке используются термины ''simulation'' и ''modelling'' (в американском языке пишется ''modeling''). Первый термин соответствует имитационному моделированию, а второй – аналитическому моделированию, хотя может применяться и для определения любого моделирования.
Математическое моделирование может осуществляться с помощью какого-либо уравнения (систем уравнений) или с помощью эквивалентных схем. Последние более наглядны и проще поддаются усложнению (введение дополнительных элементов). Эквивалентные схемы проще применению приближённых методов анализа (исключение из эквивалентных схем отдельных параметров, замена сопротивлений эквивалентным генератором э.д.с. и т.д.).
Моделирование по измеренным значениям параметров применяется для уникальных объектов, в метрологии и при научных исследованиях. Его изучает, в частности, специальная наука – "Теория планирования эксперимента".
При моделировании разрабатываемых серийных изделий в области измерительной техники, радиотехники и т.д. используются преимущественно паспортные данные элементов моделируемого объекта. В спецификациях таких элементов, как трансформаторы, диоды, интегральные схемы и т.д., одни параметры характеризуются только своими типовыми значениями; другие - только предельными с нижними, верхними или обеими границами; третьи - как предельными, так и типовыми значениями.
Моделирование по типовым значениям обычно не рассматривается в измерительной технике. Однако библиотека параметров полупроводниковых приборов для программы PSpice в работе [2] содержит только типовые данные. Моделирование по типовым значениям имеет свои достоинства. Во-первых, типовые значения приводятся в справочниках часто для гораздо большего числа параметров. Во-вторых, моделирование по типовым значениям должно соответствовать усреднённым экспериментальным показателям для сравнительно небольшого числа опытных образцов, т.е. сравнительно просто проверяется на практике. Наконец, моделирование по типовым значениям может помочь найти функциональные зависимости, которые могут использоваться для последующих расчётов по предельным значениям. Однако только моделирование по предельным значениям может дать обоснованный ответ на вопрос о целесообразности дальнейшего проектирования объекта. При этом может использоваться вероятностный подход с определённой доверительной вероятностью P или метод наихудшего случая, которому в [3] предложено приписать P = 1. В метрологии законы распределения систематических составляющих общей погрешности принято считать равномерными, а для доверительной вероятности рекомендуется обычно использовать P = 0,95 [3]. В радиоэлектронике законы распределения составляющих общей погрешности при отсутствии специальных указаний принято считать нормальными, а для доверительной вероятности обычно рекомендуется использовать P = 0,99 [4]. При расчётах погрешностей измерения параметров интегральных схем рекомендуется использовать P = 0,997 [5].
В общем случае моделирование состоит из трёх этапов: выбор модели и определение значений её параметров, выбор метода расчёта и его применение, представление результатов расчёта.
Как и моделирование, модели могут быть разделены по разным классификационным признакам [6, 7, 8]. В зависимости от уровня сигнала различают глобальные, локальные и малосигнальные модели. По частотным свойствам можно выделить статические и динамические модели. В зависимости от степени использования физических свойств объекта при моделировании, модели делятся на формальные ("чёрный ящик"), физические ("белый ящик") и модели типа "серый ящик". В первом случае физическая природа объекта практически не учитывается, во втором – является определяющей, а в третьем – учитывается при составлении уравнений, параметры которых находятся при подходе к объекту с позиций "чёрного ящика".
Методы расчёта электронных схем весьма разнообразны [7] и составляют содержание важной научной специальности "математическое моделирование". При использовании универсальных программ анализа типа P-CAD, PSpice [2] и др. инженер в значительной степени освобождается от математических проблем расчётов схем. В большинстве случаев метод расчёта становится для него своего рода "чёрным ящиком", свойства которого он может оценить при реализации соответствующих тестов, а во многих случаях может их учитывать только путём следования определённым инструкциям.
Представление результатов машинных расчётов могут быть в числах, графиках на дисплеях и т.д.
Соответствие результатов моделирования исследуемым свойствам объекта на качественном уровне описывается понятием "адекватность". В общем случае адекватность включает полноту, правильность и точность модели [9]. Применительно к моделированию большинства технических устройств адекватность обычно определяется достаточно высокой точностью расчётов.
Понять введённые выше понятия проще, если сравнить их с близкими, но гораздо полнее исследованными понятиями из метрологии.
Как известно [10], метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах обеспечения требуемой точности. Если поменять объект исследования с измерения на моделирование, то предположительно можно говорить о новой науке – "моделлогии". По аналогии с метрологией, её можно определить как науку о моделировании, методах и средствах обеспечения его единства и способах обеспечения требуемой точности. Ранее описывались некоторые общие вопросы моделирования. Перейдём теперь к вопросам обеспечения точности моделирования. Количественной мерой точности измерения в метрологии принята погрешность измерения [10]. По аналогии с понятиями из метрологии, логично использовать понятие "погрешность моделирования". Основной вопрос состоит в том, что принять за истинное значение моделируемой величины. Обычно таковым считают результат, полученный с помощью измерений на реальной системе [11]. На первый взгляд, такой подход вполне логичен и соответствует замене в метрологии истинного значения на действительное [10]. Обратимся, однако, к рис. 1. Если моделирование производится по измеренным параметрам модели (проведена её идентификация), то результаты измерения могут приближаться к истинным тем ближе, чем точнее использованные приборы. Если же используются паспортные данные, то результаты измерения на одном экземпляре могут быть весьма далеки от истинных значений при использовании сколь угодно точных приборов. В этом случае возможны только статистические оценки степени расхождения результатов моделирования и экспериментальных данных. В этом случае как нигде продуктивным является понятие "неопределённость измерения". В последнее время оно доминирует в зарубежной литературе, а в отечественной метрологии целесообразность его использования продолжает оставаться дискуссионным [10, 12].
В ряде случаев точность моделирования необходимо оценивать на стадии проектирования до изготовления устройств. Поэтому экспериментальные результаты для оценки адекватности моделирования недоступны. В этом случае возможно использование результатов моделирования на более точных моделях, принимаемых в качестве эталонных. Эти модели могут потребовать гораздо большего времени моделирования, а потому используются только в некоторых опорных точках. Если такие эталонные модели недоступны, то рекомендуется, по крайней мере, провести моделирование разными методами [10]. Близость полученных при этом результатов является косвенным подтверждением адекватности моделирования. В этой связи становится ясным целесообразность использования предварительных "ручных" расчётов до моделирования на ЭВМ, о чём говорилось выше. Используются и другие приёмы оценки адекватности [10]. Например, сходимость результатов моделирования к определённым числам при увеличении числа точек выборок.
Количественной мерой точности измерения является погрешность измерения. На практике используется и понятие "погрешность моделирования". Однако, если классификация и стандартизация терминов различных погрешностей измерения приводится как в научной [10], так и в учебной литературе (например, в [12]), то соответствующие работы в области моделирования развиты гораздо слабее. Попытаемся восполнить этот пробел, беря за основу устоявшуюся классификацию погрешностей измерения.
Точность моделирования – близость результата моделирования к истинному значению моделируемой величины.
Погрешность моделирования (ПМ) – разность между результатом моделирования и истинным значением моделируемой величины.
По месту возникновения погрешности моделирования могут быть разделены на ПМ из-за несовершенства модели, ПМ от погрешности расчёта, ПМ от погрешности отсчитывания. Последняя возникает в том случае, если результаты моделирования представляются в аналоговом виде, и обычно несущественна. ПМ из-за несовершенства модели возникает из-за погрешностей модели, но при этом не всегда равна ей, поскольку при различных условиях моделирования погрешность модели оказывает различное влияние на неё. Погрешности моделей подобны погрешностям средств измерений. Если рассматривается модель средства измерения, то погрешность его модели соответствует неточному расчёту его погрешностей. Вопрос о погрешностях моделей электронных устройств типа диода, транзистора и т.д. рассмотрен в [8]. Для экономии места на рис.2 аналогичные погрешности моделирования и модели приведены в одном прямоугольнике. Основные источники погрешностей модели: недостаточное количество параметров модели для адекватного описания реального процесса или объекта; параметры модели неточны, так как обычно являются результатами экспериментов; параметры модели выбраны некорректно. Погрешность расчёта возникает из-за несовершенства метода расчёта, из-за округлений при выполнении операций.
По способу выражения погрешность моделирования может быть представлена как абсолютная, относительная и приведённая. Абсолютная погрешность моделирования определяется как разность между результатом моделирования и истинным (или действительным) значением моделируемой величины. Относительная погрешность моделирования находиться как отношение абсолютной погрешности к истинному значению (в безразмерной форме, процентах, децибелах и т.д.). Допускается вместо истинного значения использовать действительное значение или даже результат моделирования, если относительная погрешность достаточно мала (например, менее 5%, что соответствует погрешности округления погрешности до двух значащих цифр). Приведённое значение погрешности моделирования равно отношению абсолютной погрешности моделирования к нормирующему значению моделируемой величины. Нормирующее значение моделирования ничем не отличается от нормирующего значения, задаваемого при введении норм на пределы допустимой погрешности измерения.
По характеру проявления ПМ могут быть разделены на систематическую, случайную и грубую погрешности. Систематическая погрешность моделирования – составляющая погрешности моделирования, остающаяся постоянной или закономерно изменяющаяся. Систематические погрешности являются самыми типичными погрешностями моделирования. Случайная погрешность моделирования – составляющая погрешности моделирования, изменяющаяся случайным образом. Случайные погрешности могут возникать при некорректном выборе параметров модели, например, при некорректном задании шумов элементов. Грубая погрешность моделирования – погрешность моделирования, существенно превышающая ожидаемую при данных условиях. Грубые погрешности могут возникать, например, при неправильном задании параметров расчёта.
По зависимости от скорости изменения сигнала или его частоты погрешности моделирования могут быть разделены на статическую и динамическую. Статическая погрешность моделирования не меняется при изменении скорости или частоты входного сигнала. Динамическая погрешность моделирования возникает при изменении скорости или частоты входного сигнала. Динамическая погрешность моделирования может возникать, например, из-за применения в компьютере приближённых численных методов интегрирования.
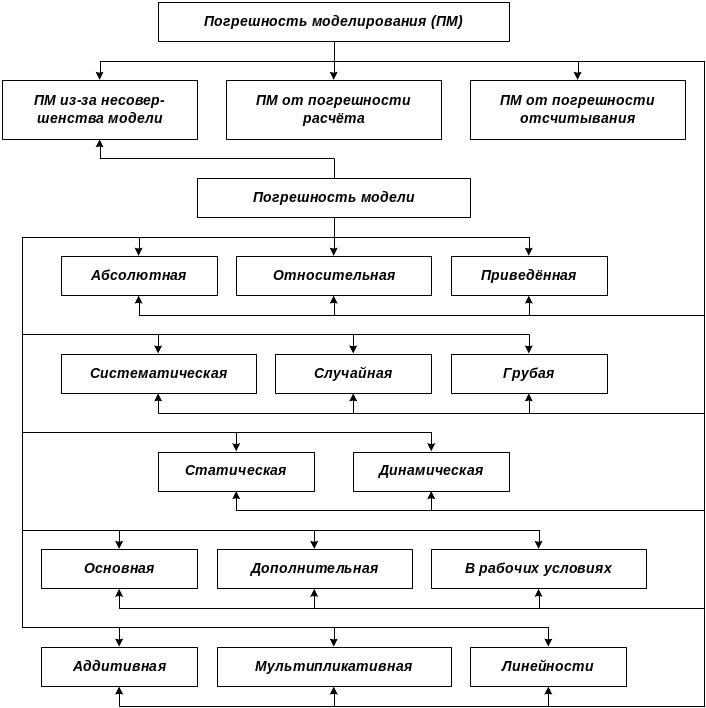
Рис. 2. Классификация погрешностей моделирования
По зависимости от влияющих величин погрешности моделирования могут быть разделены на основную, дополнительную и ПМ в рабочих условиях. Влияющей величиной при моделировании может быть, например, число точек выборок для расчёта среднего квадратического отклонения (СКО) шума моделируемого устройства. Нормальные условиями расчёта СКО, в которых определяется основная погрешность моделирования, определяются тогда при таком числе точек выборок, когда соответствующая погрешность несущественна.
По степени зависимости от входного (выходного) сигнала погрешности моделирования могут быть разделены на аддитивную, мультипликативную и линейности. Аддитивная составляющая абсолютной погрешности моделирования не зависит от значения входного сигнала, а мультипликативная составляющая абсолютной погрешности пропорциональна величине входного сигнала. Аддитивная составляющая относительной погрешности моделирования обратно пропорциональна размеру входного сигнала, а мультипликативная не зависит от него.
Из сказанного ранее следует, что основными источниками погрешности моделирования обычно являются погрешности модели. Остановимся на этом вопросе подробнее. Погрешность модели неразрывно связана с видом моделируемого объекта и его применением и/или исследованием. Основное внимание в данном курсе будет обращено на измерительные устройства или устройства, подвергаемые измерению. Рассмотрим в качестве примера однофазный двухобмоточный трансформатор. Одна обмотка, куда подаётся сигнал, называется первичной, а вторая обмотка, откуда сигнал снимается, называется вторичной. Существует большое разнообразие трансформаторов по назначению, конструкции, мощности и т.д. Если информативными сигналами на входе и выходе являются напряжения (токи), то такое устройство называется трансформатором напряжения (ТН) или тока (ТТ). Модель для обоих типов трансформаторов оказывается формально идентичный и будет рассмотрена в следующем разделе. Однако нормируемые и, следовательно, моделируемые параметры будут разными: коэффициент трансформации напряжения – в первом случае, тока – во втором. Соответственно в первом случае будет важна точность моделирования коэффициента трансформации напряжения, во втором - точность моделирования коэффициента трансформации тока. Как будет показано в следующем разделе, разные параметры модели трансформатора будут существеннее для моделирования ТН или ТТ. Важным вопросом для выбора модели и, соответственно, для анализа погрешностей моделирования, является метод измерения параметров модели (метод идентификации). Если, например, параметры модели трансформатора определяются на фиксированной частотой, то применение параллельного или последовательного включения сопротивления и индуктивности не имеет принципиального значения. Однако при идентификации в широком частотном диапазоне неправильный выбор указанной цепочки резко повысит погрешность модели. Погрешность модели может быть в общем виде определена как погрешность того или иного параметра модели. Если, например, используется модель в виде эквивалентной схемы, то погрешность данной модели может описываться как погрешности того или иного параметра данной эквивалентной схемы. Если, например, рассматривается ТН, то его моделью со стороны первичной обмотки в режиме короткого замыкания вторичной обмотки является типично эквивалентная схема, состоящая из последовательного соединения сопротивления и индуктивности. При фиксированной частоте, температуры и т.д. погрешность данной модели может характеризоваться тем, что значения сопротивления и индуктивности были определены неточно. Если частота, температура и другие влияющие величины отличаются от тех, при которых производилось определение указанных параметров, то образуются соответствующие дополнительные погрешности модели. Для уменьшения частотной погрешности эквивалентная схема может быть усложнена, например, путём шунтирования индуктивности сопротивлением. Исходная модель имела две степени свободы (переменные, которые можно менять независимо друг от друга) и позволяла теоретически абсолютно точно смоделировать (предсказать) активную и индуктивную составляющие импеданса короткого замыкания на одной частоте, например, на 50 Гц. Новая модель имеет уже три степени свободы. Поэтому появляется возможность теоретически абсолютно точно предсказать значения активной и индуктивной составляющей при трёх частотах, например на постоянном токе и при частоте 50 Гц. Однако на другой частоте, например, 1000 Гц может появиться частотная погрешность – активная и индуктивная составляющие данной модели могут отличаться от действительных значений. Этот недостаток можно исправить, если использовать эквивалентную схему из пяти элементов: последовательного соединения сопротивления и двух цепочек из параллельного соединения сопротивления и индуктивности. Эта схема имеет уже три степени свободы. Поэтому появляется возможность устранить частотную погрешность для постоянного тока и двух частот. На приведённом примере можно понять понятие иерархия моделей. Первая модель является частным случаем второй, вторая –частный случай третьей. Модель стоящая на более высоком уровне является эталонной (образцовой) для модели более низкого уровня. Например, описанная выше модель из трёх элементов может рассматриваться как эталонная для модели из двух элементов; описанная выше модель из пяти элементов может рассматриваться как эталонная для модели из трёх элементов. Для определения погрешности модели из двух элементов на всех частотах помимо той, на которой были определены её сопротивление и индуктивность, надо рассчитать активное и индуктивное сопротивления на этих частотах для эталонной модели, состоящей из трёх или (точнее) из пяти элементов. Возникает вопрос, на какой модели можно остановиться. Это не простой вопрос. В какой-то степени он эквивалентен выбору числа членов в ряде Тейлора. Чаще всего в измерительной технике ограничиваются первыми производными, не всегда давая строго математического обоснования. Применительно к моделям ограничивающим фактором на практике является сложность модели и методов её идентификации. Во многих случаях удаётся проверить точность моделей с помощью соответствующих экспериментов. В нашей классификации это означает переход от математического моделирования к физическому моделированию. При составлении более сложных моделей необходимо учитывать также повышение сложности её идентификации. Кроме того, возникает проблема её реализуемости. Например, если активная и индуктивная составляющая импеданса КЗ для ТН меняется слишком быстро для двух частот при её идентификации, то модель из пяти элементов может в принципе не обеспечить нулевой погрешности на этих частотах. В этом случае приходится решать, для каких часто важнее получить минимум погрешности модели. Та или иная погрешность модели может по-разному влиять на погрешность моделирования. Например, простейшая из рассмотренных выше моделей ТН, может давать в принципе абсолютно точные результаты моделирование проводится на той же частоте, на которой проводилась идентификация этой модели. На практике может даже в этом случае возникать погрешность моделирования из-за несовершенства расчётов. Студенты и молодые инженеры часто игнорируют эту погрешность, считая, что компьютер («машинка») не ошибается. Это очень печальное заблуждение.
Различают теоретическую и законодательную метрологию [10]. Приведённые выше соображения по различным аспектам моделирования можно отнести к теоретической моделлогии (последний термин был предложен нами выше как предварительный, рабочий). Рассмотрим теперь состояние дел в области законодательной моделлогии. Работа в этой области начата недавно и ещё не получила достаточно широкого развития, особенно при моделировании измерительных устройств. Законодательно были указаны нормируемые метрологические характеристики средств измерений [3], которые позволили бы проводить оценку погрешности средств измерений в реальных условиях эксплуатации. В наших терминах наличие указанных характеристик и методик позволяло бы осуществлять моделирование погрешностей в узаконенном порядке. Хотя предложенные характеристики не были приняты в полном объёме, многие рекомендации из [3] и других стандартов используются при моделировании погрешности измерения и её доверительного интервала [12]. Оценка неопределённости измерения, о которой говорилось выше, представляет собой стандартизацию упрощенного моделирования точности измерения. Потенциально важным является стандартизация понятия верификации модели – проверки её соответствия определённым требованиям. Представление объективных данных о выполнении в результате моделирования заданных функций содержится в стандартизованном понятии "валидация". В [13] валидацию предложено на основании стандартизованных процедур переводить в оценки по шести бальной системе (отлично, очень хорошо, хорошо, удовлетворительно, плохо, очень плохо). Этот подход заслуживает, на наш взгляд, внимания, так как перекидывает мост от специалистов к потребителям.
