Билет №5
1) Коэффициент корреляции, условия и возможности его использования в геологии.
Коэффициент корреляции определяет тесноту линейной связи между двумя величинами. Его значения изменяются от -1 до +1. При r = 0 связь между величинами отсутствует. При \r\ = 1 связь функциональная. Знак ± показывает, прямой, или обратной пропорциональной является взаимосвязь.
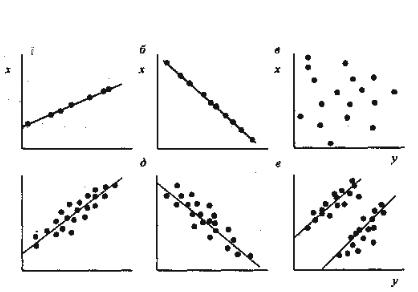
Коэффициент корреляция подсчитывается по формуле:
где N - общее количество точек, n1,3 - количество точек в квадрантах 1 III, n2,4 - то же, в квадрантах II и IV.
широко используются в геологической практике.
Коэффициенты корреляции широко используются в геологической практике. Так как в геологической практике обычно приходится иметь дело не с одной, а одновременно с несколькими случайными величинами. Например, при опробовании золоторудной жилы одновременно производят замеры ее мощности, определяют содержание сульфидов, цвет кварца, степень брекчирования, элементы залегания и т.п. Эти изучаемые свойства могут быть независимы, но могут быть и определенным образом взаимосвязаны. Задача исследователя состоит в том, чтобы установить, есть ли эта связь, и, если есть - рассчитать уравнение зависимости.
2)Непараметрические критерии для проверки гипотезы о равенстве двух неизвестных средних.
В случае если закон распределения случайных величин неизвестен, следует воспользоваться непараметрическими критериями Ван-дер-Вардена, Вилкоксона, или Манна-Уитни.
Пример
Применение критерия Манна-Уитни. Как и во всех критериях подобного типа, вычислительные операции проводится не с самими числами, а с их рангами.
Допустим, мы имеем две выборки Х и Y объема n и m и хотим проверить гипотезу о том, что они принадлежат к одной и той же совокупности. Объединим две выборки и расположим все значения в порядке возрастания – от меньшего к большему. Наименьшее значение при этом получит ранг 1, наибольшее – ранг (n+m). Если выборки принадлежат одной совокупности, то естественно ожидать, что ранги одной из выборок будут достаточно равномерно рассеяны в общей последовательности рангов. Критерий Манна-Уитни вычисляется по формуле:
Т
=
(37)
Первый член – это сумма рангов наблюдений первой выборки, п – число наблюдений в первой выборке. Критические значения Т для нижнего критического предела приведены в таблице 5 приложения к данному пособию. Предел для верхней критической площади определяется выражением Т1-α = п * т - Тα. Например, если в нашем случае п = 8, т = 10, вычисленное значение Т = 35, а уровень значимости 10%,то нижний критический предел будет равен: Т0,05 = 21, верхний предел Т0,95 = 8 *10–21=59. Вычисленное Т не выходит за эти пределы, следовательно, с вероятностью 90% можно утверждать, что выборки не различаются, то есть принадлежат одной совокупности.
Билет №6
1)Корреляции, условия и возможности его использования в геологии.
Коэффициент корреляции определяет тесноту линейной связи между двумя величинами. Его значения изменяются от -1 до +1. При r = 0 связь между величинами отсутствует. При \r\ = 1 связь функциональная. Знак ± показывает, прямой, или обратной пропорциональной является взаимосвязь.
Коэффициент корреляция подсчитывается по формуле:
где N - общее количество точек, n1,3 - количество точек в квадрантах 1 III, n2,4 - то же, в квадрантах II и IV.
широко используются в геологической практике.
Коэффициенты корреляции широко используются в геологической практике. Так как в геологической практике обычно приходится иметь дело не с одной, а одновременно с несколькими случайными величинами. Например, при опробовании золоторудной жилы одновременно производят замеры ее мощности, определяют содержание сульфидов, цвет кварца, степень брекчирования, элементы залегания и т.п. Эти изучаемые свойства могут быть независимы, но могут быть и определенным образом взаимосвязаны. Задача исследователя состоит в том, чтобы установить, есть ли эта связь, и, если есть - рассчитать уравнение зависимости.