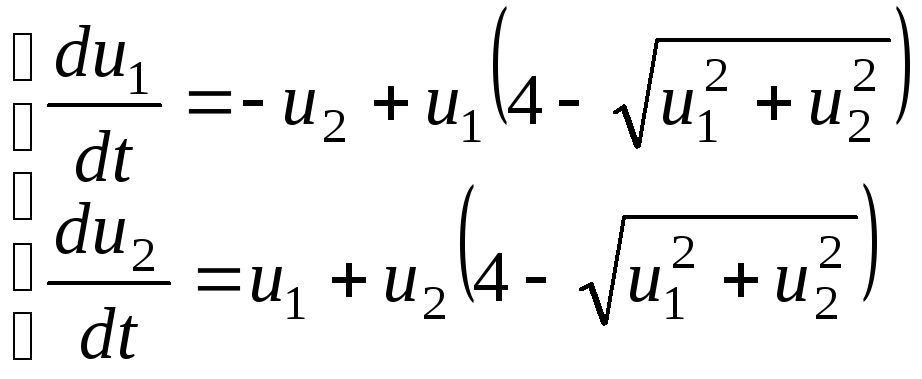МатМод-ЛАБА3

ЛАБОРАТОРНАЯ РАБОТА № 3

Тема работы: Анализ периодических режимов функционирования нелинейной динамической системы. Устойчивые предельные циклы.

Цель работы: На модельных примерах нелинейных динамических систем научится анализировать автоколебательные режимы функционирования технических объектов и возможность перехода из одного стационарного режима в другой стационарный режим.

Задание: Задана нелинейная автономная система обыкновенных дифференциальных уравнений, описывающая эволюцию некоторой технической системы.

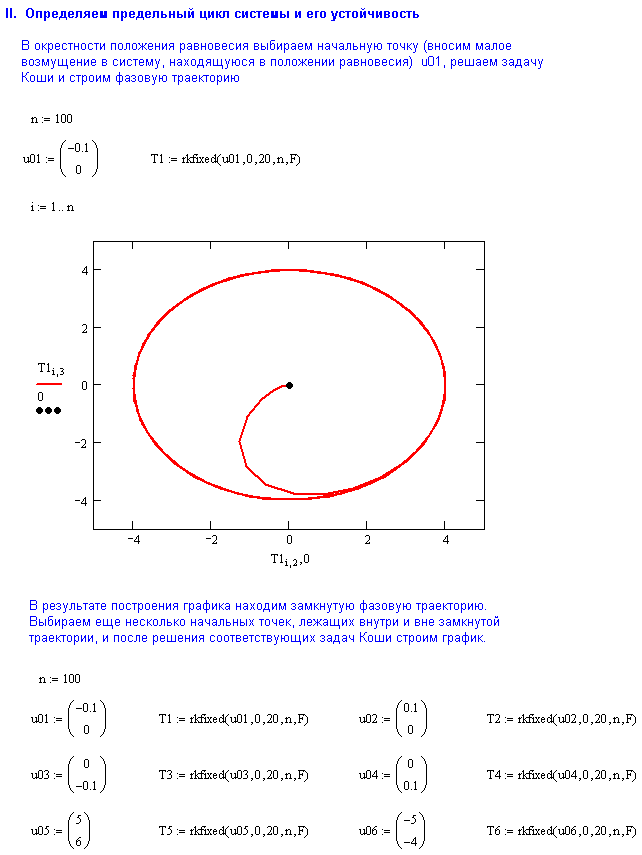
Покажите графически, что данная система имеет предельный цикл в пространстве фазовых переменных; определите тип предельного цикла (устойчивый, неустойчивый, полуустойчивый). Сделайте заключение о возможности перехода системы в автоколебательный режим движения при нарушении условий равновесия.

Фазовые траектории начинайте строить в окрестности положения равновесия системы (если оно неустойчиво) или в окрестности указанной в задании точки .

Теоретическая часть

Рассмотрим автономную динамическую систему второго порядка

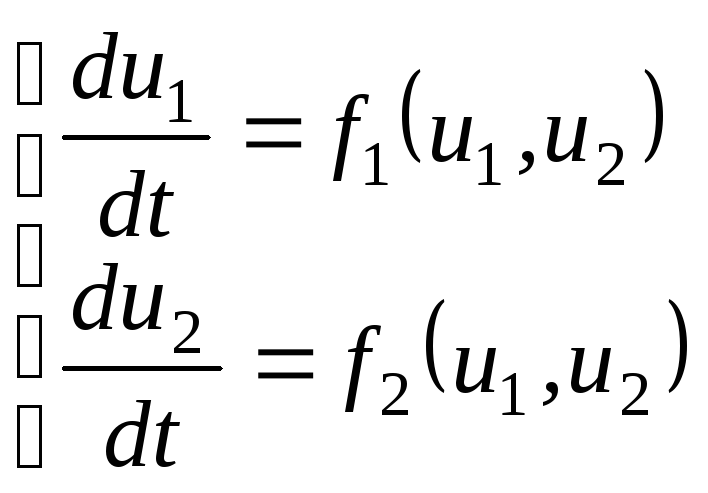, (1)

где - время, - фазовые координаты. Правые части системы уравнений, т.е. функции , предполагаются непрерывно дифференцируемыми.

Наряду с положениями равновесия системы, которые определяются как решения уравнений

, , (2)

исключительно важную роль в анализе возможных режимов функционирования технических объектов играют предельные циклы – замкнутые изолированные фазовые траектории. (Замкнутая фазовая траектория называется изолированной, если существует такая достаточно малая (кольцеобразная) ее окрестность, внутри которой нет других замкнутых фазовых траекторий).

Все траектории, которые начинаются в малой окрестности предельного цикла, обладают тем свойством, что спиралевидно приближаются к нему либо при , либо при . В зависимости от этого предельные циклы подразделяются на следующие типы:

устойчивые – близкие траектории при «навиваются» на цикл;

неустойчивые – близкие траектории при «уходят» от цикла («навиваются» на него при );

полуустойчивые – траектории, лежащие по одну сторону от цикла, «навиваются» на него при , а лежащие по другую сторону – «уходят» от него («навиваются» на цикл при ).

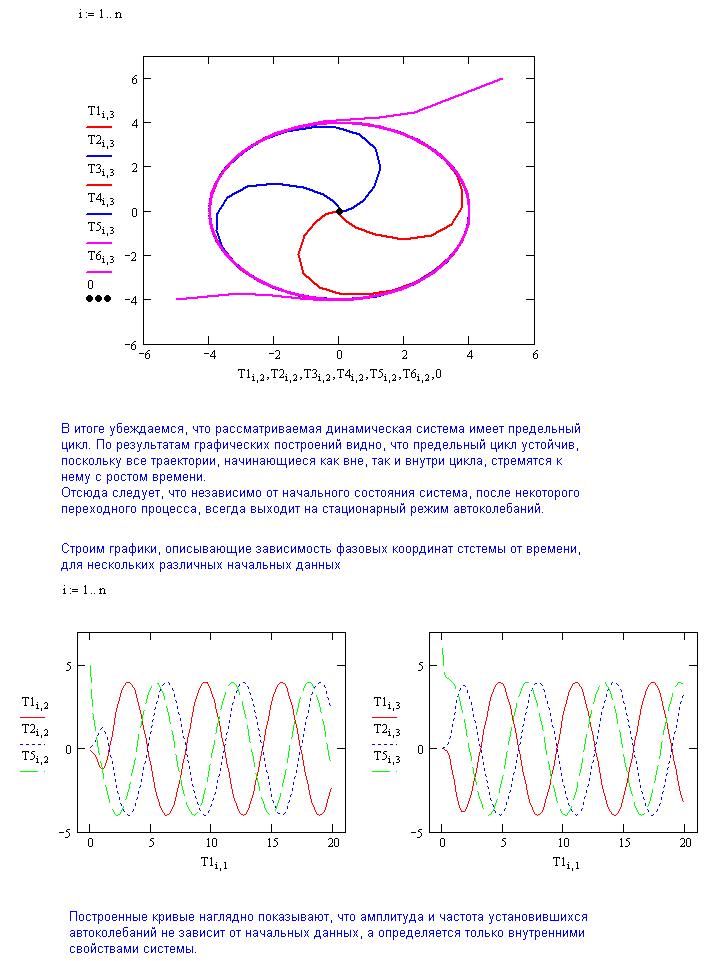
Устойчивый предельный цикл – это математический образ автоколебаний технических систем. Таким образом, вопрос о существовании автоколебаний сводится к вопросу о существовании устойчивого предельного цикла системы уравнений (1). Размеры и форма предельного цикла определяют амплитуду и характер колебаний, а время одного оборота изображающей точки по циклу – период колебаний. При наличии устойчивого цикла устанавливаются периодические колебания, параметры которых не зависят от начальных условий, а полностью определяются внутренними параметрами технической системы.

Простейшими примерами автоколебательных физических процессов являются: периодические электромагнитные колебания в ламповом генераторе, работа часового механизма, звучание духовых и смычковых музыкальных инструментов.

Важно помнить, что автоколебания принципиально отличаются от других колебательных процессов. Основные характерные особенности автоколебательного процесса:

автоколебания возможны только в нелинейных неконсервативных (диссипативных) автономных системах;

автоколебания поддерживаются за счет энергии, которая подводится к системе от внешних источников неколебательного характера;

в системе происходит самовозбуждение колебаний;

частота и амплитуда установившихся автоколебаний зависит только от параметров системы и не зависит от начальных условий;

фаза автоколебаний – произвольна.

Напомним, что при свободных колебаниях

частота определяется параметрами системы,

амплитуда и фаза – начальными условиями;

при вынужденных колебаниях

частота определяется внешней (периодической) силой,

амплитуда и фаза зависят как от параметров системы, так и от внешней силы.

При разработке математической модели автоколебательной системы и ее содержательном анализе полезно различать следующие элементы системы:

основную колебательную систему,

внешний источник энергии,

обратную связь (между колебательной системой и источником энергии), управляющую поступлением энергии в систему.

Можно привести многочисленные примеры технических систем, которые являются потенциальными автоколебательными системами. Основной невозмущенный режим работы таких систем является неколебательным, но при некоторых условиях может возникнуть неустойчивость невозмущенного движения и нарастающий переходный процесс, приводящий к автоколебаниям. Автоколебания вызывают нежелательные динамические нагрузки и даже могут привести к разрушению машин или приборов.

Отметим классический и срывной флаттер (возникают в результате аэродинамических нагрузок). Классическому флаттеру подвержены крылья, хвостовое оперение и элероны самолетов, срывному флаттеру – лопатки турбомашин, лопасти воздушных винтов и многие инженерные сооружения, находящиеся в ветровом потоке: висячие мосты, надземные трубопроводы, дымовые трубы, конструкции башенного типа и т.п. Другим примером (потенциальной автоколебательной системы) являются металлорежущие станки. При некоторых режимах резания лезвийным инструментом может возникнуть неустойчивость режима резания, приводящая к стационарным вибрациям (автоколебаниям).

В приведенных примерах автоколебания являются крайне нежелательным явлением. Задача анализа математических моделей состоит в том, чтобы обеспечить такие режимы работы технических систем, при которых невозмущенное движение всегда было бы устойчивым.

Порядок выполнения задания

1. Присвойте переменной ORIGIN значение, равное единице.

2. Решите систему нелинейных уравнений (2) и определите координаты положения равновесия системы в плоскости фазовых переменных .

3. Определите частные производные от правых частей системы уравнений (1); вычислите их значения в положении равновесия и сформируйте матрицу Якоби.

4. Вычислите собственные значения матрицы Якоби и определите характер положения равновесия системы.

5. Выбрав начальную точку в окрестности положения равновесия (если оно неустойчиво) или в окрестности указанной в задании точки , решите (с использованием встроенной функции rkfxed) задачу Коши. Количество узлов интегрирования и длину интервала интегрирования подберите самостоятельно, так чтобы прояснить вопрос о существовании предельного цикла.

6. Обнаружив предельный цикл, постройте еще две фазовые траектории с началом внутри цикла и две траектории с началом вне цикла.

6. Изобразите все фазовые траектории на одном графике. По результатам графических построений определите тип цикла.

7. В случае устойчивого предельного цикла убедитесь в том, что амплитуда и частота автоколебаний не зависит от начальных условий. Для этого постройте несколько графиков .

8. Сохраните рабочий документ.

В приведенном ниже примере предполагается, что динамическая система описывается системой дифференциальных уравнений: