2)Полигармонический анализ.

Геологические объекты очень часто обладают периодическим харак­тером изменчивости свойств. Периодичность нередко отмечается в разме­щении тектонических нарушений, в пространственном распределении со­держаний различных элементов, физических свойств пород, в составе осадочных и метаморфических толщ и т.д. Естественно, периодические колебания при этом осложняются и затушевываются случайными, нерегулярными, флуктуациями.

Для выделения и описания периодической закономерной составляющей изменчивости обычно применяется модель полигармонической случайной функции. Мате­матическое ожидание этой функции выражается тригонометрическим поли­номом вида:

Мх(l) = А₀ + , (87)

где А₀ - константа, V - количество гармоник, А_к , ω_к , φ_к - соответственно, амплитуда, частота и фаза каждой гармоники.

С помощью этой модели любой ряд значений признака, при равном расстоянии между точками ( r ), можно описать функцией:

х( r ) = Мх( r )+h_х( r ) , (88)

где h_х(r ) - случайная составляющая, осложняющая периодические колебания.

Модель полигармонической случайной функции наиболее универсаль­на из всех рассмотренных нами ранее моделей. При отсутствии периоди­ческой составляющей она превращается в модель стационарной случайной функции, а при отсутствии автокорреляции - в обычную статистическую модель.

Таким образом, чтобы выявить закономерную составляющую периоди­ческого явления, необходимо правильно подобрать амплитуды, частоты и фазы соответствующих гармоник, отражающих периодичность разных поряд­ков. Подобная операция широко применяется в радиотехнике (частотная модуляция) и других областях техники. В настоящее время разработано множество методов и специальных приборов для выявления скрытых перио­дичностей (14).

Р

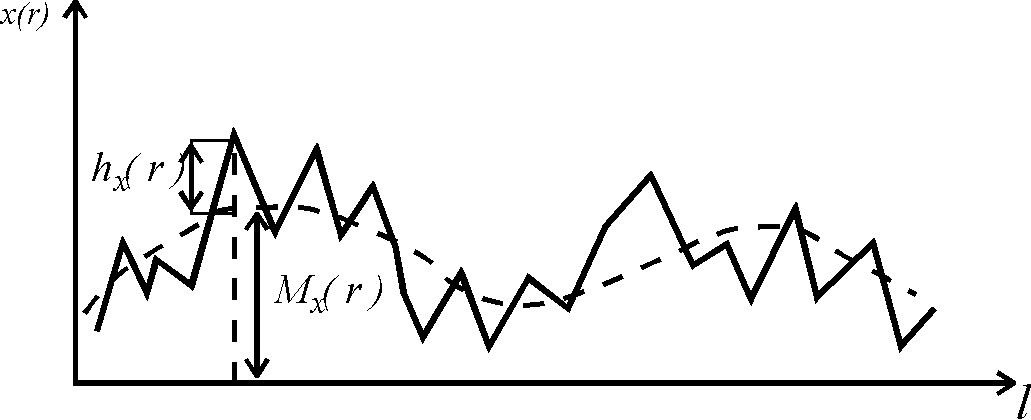
ис. 33. Сглаживание эмпирических наблюдений

тригонометри­ческой функцией

(показана только одна гармоника)

В геологии обычно используют метод, основанный на оценке спект­ральной плотности дисперсии S_х(ω ), получаемой в результате разло­жения в ряд Фурье корреляционной функции:

S_х(ω) = (89)

Для дискретного ряда наблюдений спектральная плотность заменяет­ся линейчатым спектром амплитуд. Каждое значение линейчатого спект­ра вычисляется по формуле:

d_к = , (90)

где А_к - амплитуда к-й гармоники. Сумма амплитуд всех к гармоник равна при этом 1. Рассмотрим для наглядности графическое изображе­ние названных характеристик (рис.34).

На левом графике мы видим, как общая дисперсия признака распределя­ется по частотам колебаний (общая площадь равна полной дисперсии). Правый график отражает распределение общей дисперсии между отдельны­ми гармониками. Здесь ω - число периодов, приходящихся на длину профиля.

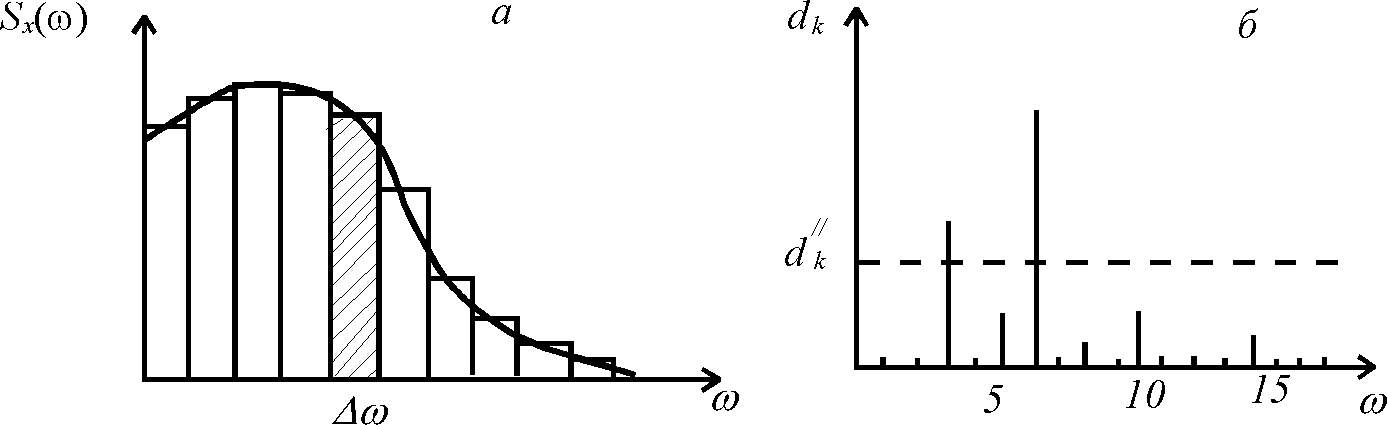
Рис. 34. Графики спектральной плотности дисперсии (а)

и частотного спектра амплитуд (б)

Значение d´´_к, определяющее уровень случайных флуктуаций, опре­деляется по формуле (для 5% уровня значимости):

d´´_к = , (91)

где N - число значений спектра амплитуд. Отсюда можно с наперед заданной доверительной вероятностью проверить гипотезу о принадлежно­сти тех или иных пиков спектра к случайным колебаниям.

Доля закономерной составляющей в общей изменчивости вычисляется по формуле:

S´ = - , (92)

где d_к(аном.) - сумма значений спектра, N - число значений спектра, т - число аномальных значений спектра.

Вычисленные значения спектра амплитуд подставляют в тригонометричес­кий полином и получают соответствующее уравнение регрессии, для кото­рого аргументом является координата пространства (или время).