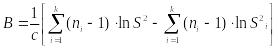2)Понятие о статистических гипотезах. Ошибки 1-го и 2-го рода. Доверительная и критическая области критерия, уровень значимости.

Под статистическимипонимаются такие гипотезы, которые относятся либо к виду, либо к отдельным параметрам распределения случайной величины. Например, статистической является гипотеза о том, что веса проб, отобранные одним человеком по одной методике распределены по нормальному закону.

Поскольку выборочные данные ограничены по объему и носят слу­чайный характер, при обосновании выводов по статистическим данным вполне возможны ошибочные заключения. При этом ошибки могут быть двух видов:

1) если гипотеза, являющаяся правильной, не принята - это ошибка 1-го рода,

2) если принята ложная гипотеза - ошибка 2-го рода.

Проверяемая гипотеза обычно обозначается Н₀ и называется нуле­вой, конкурирующая или альтернативная гипотеза обозначаетсяН₁. Например:Н₀:μ₁= μ₂;Н₁: μ₁ μ₂.

Уровень значимости q определяет вероятность ошибки 1-го рода, и, казалось бы, надо брать q, как можно меньше. Но, к сожалению, это далеко не всегда оправдано.

Рассмотрит альтер­нативу Н₁:μ₁ μ₂ . Очевидно, что событие t Т₀ при условии, что верна Н₁, будет способствовать ошибочному решению, т.е. принятию гипотезы Н₀, хотя она не верна. Эта ошибка 2-го рода, и она тем больше, чем мень­ше q.

Ее вероятность обозначена β, вероятность ошибки 1-го рода обозначена α.

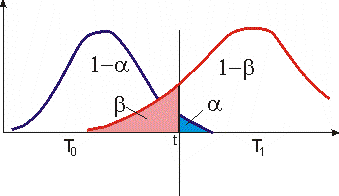
Очевидно, надо стремиться, чтобы α и β примерно уравновешивались. В геологии обычно очень трудно оценить вероятность ошибки 2-го рода, поэтому во всех случаях формального выбора доверительная область ограничивается уровнем значимости 5% (то есть доверительной вероятностью 95%).

Билет №4

1)Методы проверки гипотезы о соответствии распределения теоретическому закону.

I. О соответствии эмпирического распределения теоретическому закону

II. О равенстве неизвестных средних

III. О равенстве неизвестных дисперсий

О соответствии эмпирического распределения теоретическому закону

Критерий Пирсона:

Для проверки гипотезы разбиваем область выборочных значений х₁,х₂, х_3, .. х_n на k интервалов, необязательно равных, и подсчитываем частоты попадания значений выборки в эти интервалы n_i

Затем подсчитываем теоретические частоты попадания значений в эти интервалы: N_i= N·P_i, здесь

N – общее число значений в выборке;

P_i=F₀(а_i+1) -F₀(а_i); (F₀(t)– табличное значение проверяемой функции распределения в точке t .

a_i,а_i+1 - границы интервалов.

Затем вычисляем значение критерия:

χ² =

Если вычисленное значение χ²больше, чем χ²_q,_{k -3}, взятое из таблицы χ²-распределения, то гипотезаНо отклоняется, т.е. счита­ем, что распределение не соответствует проверяемому закону (при заданном уровне значимости q).

Упрощенный критерий соответствия распределения нормальному закону:

При нормальном распределенииА=0и Е=0. Следовательно, отклонение от нуля выборочных значений А и Е не должно превышать t*SAи t*SE. Здесьt – табличное значение функции нормального распределения при заданной доверительной вероятности.

Обычно принимают t=3, что соответствует 99% доверительной вероятности.

Критерий соответствия распределения нормальному закону:

О равенстве неизвестных средних

а) Проверка гипотезы о равенстве двух неизвестных средних

При нормальном законе распределения и соблюдении неравенства δ²₁ δ²₂применяют параметрический кри­терий Стъюдента:

t =

Если вычисленное t>t_q,(n1+n2-2), взятого из таблицы распределения Стъю­дента, то гипотеза о равенстве неизвестных средних отвергается.

В противном случае расхождение считается незначимым и принимается гипотеза о равенстве неизвестных средних.

Если выяснится, что δ²₁=δ²₂, то критерий Стьюдента следу­ет применять в следующем виде:

t=

где S = .

Критическое значение t_q,_{n1 +n2 -2} при этом также берется из таб­лицы распределения Стьюдента.

Если распределение случайной величины логнормальное, то следует использовать критерий Д. А. Родионова (при δ²₁ δ²₂)

t =

где S²₁ и S²₂ -дисперсии распределения логарифмов значений, полученные по выборкам. Крити­ческое значение t_qнаходится по таблице функции нормального рас­пределения F(t).

Если выяснится, что δ²₁ = δ²₂, то можно использовать критерий Стьюдента,заменив и , на ln , и ln .

Если закон распределения случайных величин неизвестен, следует воспользоваться непараметрическими критериями (Ван-дер-Вардена, Вилкоксона, Манна-Уитни и т.д.).

Рассмотрим пример применения критерия Манна-Уитни. Как и во всех критериях подобного типа, вычислительные операции проводится не с самими числами, а с их рангами (порядковыми номерами).

Допустим, мы имеем две выборки Х и Y объема nи m и хотим проверить гипотезу о том, что они принадлежат к одной и той же совокупности. Объединим две выборки и расположим все значения в порядке возрастания – от меньшего к большему. Наименьшее значение при этом получит ранг 1, наибольшее – ранг (n+m). Если выборки принадлежат одной совокупности, то естественно ожидать, что ранги одной из выборок будут достаточно равномерно рассеяны в общей последовательности рангов.

Ранговый (непараметрический) критерий Манна-Уитни имеет вид: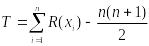

Проверка гипотезы о равенстве k неизвестных средних

при нормальном законе распределения:

1) если дисперсии равны:

2) если дисперсии не равны:

Если вычисленное значение νпревы­сит табличное значение χ²_q,k-1 взятое из таблиц χ²-распределения, то гипотеза о равенстве k средних отвергается.

О равенстве неизвестных дисперсий

а) проверка гипотезы о равенстве двух дисперсий при нормальном распределении (критерий Фишера):

б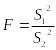 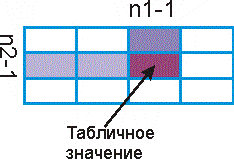) проверка гипотезы о равенстве k дисперсий при нормальном распределении (критерий Бартлета):