Билет №3

1)Точечные и интервальные оценки параметров распределения по выборочным данным при нормальном и логнормальном законах распределения.

Полученные по выборочным данным приближенные характеристики каких-либо свойств изучаемой совокупности называются их оценками. Например, в качестве оценки неизвестного среднего значения чаще всего используется среднее арифметическое по выборке, хотя возможны и другие варианты оценок этого параметра: среднее геометрическое, среднее гармоническое и др.

Статистические оценки могут быть точечными и интервальными. При точечной оценке неизвестная харак­теристика оценивается некоторым числом, а при интервальной оценке указывается некоторый интервал значений, в пределах которого с заданной вероятностью должно находиться истинное значение оценивае­мой величины.

Полученные по выборочным данным приближенные характеристики каких-либо свойств изучаемой совокупности называются их оценками. Например, в качестве оценки неизвестного среднего значения чаще всего используется среднее арифметическое по выборке, хотя возможны и другие варианты оценок этого параметра: среднее геометрическое, среднее гармоническое и др.

Статистические оценки могут быть точечными и интервальными. При точечной оценке неизвестная харак­теристика оценивается некоторым числом, а при интервальной оценке указывается некоторый интервал значений, в пределах которого с заданной вероятностью должно находиться истинное значение оценивае­мой величины.

Точечные оценки должны удовлетворять требованиям сос­тоятельности, несмещенности иэффек­тивности.

Состоятельной называется оценка, сходящаяся по вероятности к оцениваемому параметру с увеличением объема выборки:

.

Несмещенной называется оценка, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки (т.е. нет си­стематической ошибки).

Эффективной называется оценка, обладающая минимальной дисперсией из всех возможных оценок. Такая оценка (если она не смещена) наиболее предпочтительна, так как обеспечивает максимально тесную группировку результатов около ис­тинного значения неизвестного параметра.

Наиболее важными характеристиками случайной величины являются математическое ожидание и дисперсия.

При нормальном законе распределения состоятельной, несмещенной и эффективной оценкой математического ожидания случайной величины яв­ляется среднее арифметическое( ),полученное по выборочным данным.

При логнормальном распределении не является эффективной за счет разброса больших значений, поэтому в практике геохимических работ в этом случае обычно используютсреднее геометрическое:

= .

Выборочная оценка дисперсии(S²) при нормальном законе распре­деления определяется по формуле:

S²= .

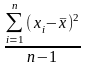При логнормальном законе распределения в качестве оценки среднеквадратического отклонения обычно используют стандартный множитель ε:

ε = е^S(ln)

Точечная оценка не содержит информации о точности полученного результата. Чем меньше выборка и чем больше изменчивость признака, тем большей может оказаться ошибка определения точечной оценки. Поэтому желательно знать тот интервал значений, в который с за­данной вероятностью попадает истинное значение изучаемого признака.

Согласно центральной предельной теореме, доверительный интер­вал, внутри которого с заданной вероятностью будет находиться истин­ное значение математического ожидания, для выборочных данных определяется из соотношения:

λ = ± .

Число t зависит от выбранной доверительной вероятности. Это не что иное, как аргумент табличной функции Ф(t), поэтому его всегда можно найти по таблице.

Если объем выборки менее60, то характер распределения величи­ныt зависит не только от Мхиσ_x, но и от объема выборки. Такое распределение называется распределением Стьюдента. Числоt в этом случае находится не из таблицы функции Ф(t), а из таблицы рас­пределения Стьюдента.

Таким образом, число t показывает, сколько раз надо отложить S влево и вправо от , чтобы накрыть истинное значение M(x) с вероятностью р.

Интервальная оценка дисперсии.

Выборочная оценка дисперсии, как случайная величина, представляющая собой сумму квадратов независимых случайных величин, каждая из которых подчиняется нор­мальному закону распределения с параметрами (0,1), называется слу­чайной величиной сχ²- распределением иk =n степенями свободы.

Для функции распределения χ² составлены таблицы, по которым можно вычислить вероятность того, что случайная величи­на, подчиняющаяся закону χ², не превысит фик­сированного значения χ²_k,α .

Доверительный интервал для дисперсии определяется из выражения:

<δ²