2)Проверка гипотезы о линейном характере корреляционной связи.

Коэффициент корреляции определяет тесноту линейной связи между двумя величинами. Его значения изменяются от -1 до +1. При r = 0 связь между величинами отсутствует. При \r\ = 1 связь функциональ­ная. Знак ± показывает, прямой, или обратной пропорциональной явля­ется взаимосвязь.

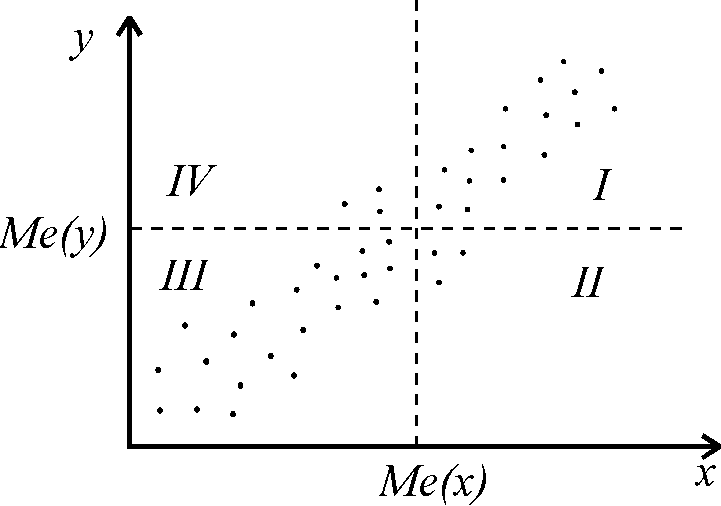
Рис. 16. Определение коэффициента корреляции графическим путем

Следовательно, проверка гипотезы о наличии корреляционной связи заключается в оценке значимости отли­чия от нуля вычисленных по выборке значений r :

Н₀ : ρ = 0 ; Н₁ : ρ 0.

Критерий для оценки значимости отличия r от 0 предложен Фише­ром:

t = .

Если вычисленное значение t больше, чем ,_n-2 взятое из таблицы распределения Стьюдента, то отличие r от 0 признается значимым. В геологической практике иногда пользуются упрощенным кри­терием:

= 2 (для уровня значимости 0,05).

Во многих руководствах по математической статистике и задачни­ках по геохимии есть специальные таблицы критических значений коэффи­циента корреляции в зависимости от числа наблюдений N (16).

К сожалению, коэффициент корреляции очень чувствителен к виду функции распределения величин, входящих в двумерную систему. Поэтому, если эти распределения отличаются от нормальных и не поддаются норма­лизации, для проверки гипотезы о наличии корреляционной связи следу­ет использовать ранговый коэффициент кор­реляции Спирмена. При этом каждому значению х и у присваи­вается ранг в порядке возрастания их значений. Если значения повто­ряются, им присваивается средний между повторяющимися значениями ранг. Выражение для r имеет вид:

r = 1 - , (51)

где n - количество пар значений в выборке, d - разность рангов со­пряженных значений х и у .

Для оценки значимости отличия рангового коэффициента корреляции от 0 существует специальная таблица критических значений (1, 16). Можно также воспользоваться выражением:

r _крит. =

где φ(р) - значение обратной функции нормального распределения при доверительной вероятности р (берется из таблицы).

Если вычисленное значение r окажется больше r _крит. , отличие его от нуля считается значимым. В противном случае считаем, что ли­нейная связь между величинами не установлена.

Билет №15

1)Моделирование пространственной изменчивости. Тренд-анализ.

Тренд-анализ - аналитические методы исследования пространственной изменчивости. С помощью тренд-анализа решается три типа задач:

1)проверка гипотезы о наличии какой-либо закономерности в прост­ранственной изменчивости параметра; 2)выделение и описание наи­более общих закономерностей (поверхностей тренда); 3) выявление отклонений от поверхностей тренда (так называемых "аномальных" участков, или «остатков» тренда).

Проверка гипотезы о наличия тренда заключается в сравнения полученной эмпирической последовательности значений признака с такой теоретической последовательностью, в которой закономерная составляющая заведомо отсутствует.

Обычно наличие тренда проверяется двумя простыми способами: а) смены знака и б) количества скачков.

Точкой смены знака называется такой элемент последовательнос­ти, в котором знак приращения изменяется на противоположный. В слу­чайной последовательности математическое ожидание числа точек смены знака определяется выражением:

М(t) = , (74)

где N - общее количество наблюдений. Значимость отличия эмпирически подсчитанного числа точек смены знака ( t ) от теоретического ( М( t )) определяется по критерию:

Z = , (75)

где δ²_t = .

Если Z < -1,65 (для 5% уровня значимости), то тренд существует. В противном случае считаем, что закономерная составляющая прост­ранственной изменчивости отсутствует.

Метод скачков заключается в том, что вся последовательность де­лится на "скачки", представляющие собой группы соседних элементов последовательности, имеющих один знак - "+" (если все значения боль­ше медианы) или "-" (если значения признака меньше медианы).