Расчет вариантов группирования

№ шага	Число групп	Элементы групп	dТ	hmin	аrccos rкрит
1	4	Pb, Zn	0,64	0,80	1,24 для 95 %
2	3	Ni, Cr	0,80	1,22	1,14 для 99 %
3	2	Pb, Zn, Co	1,02	1,35
4	1	Pb, Zn, Co, Ni, Cr	1,20	-

Для большей наглядности результаты группирования можно предста­вить в виде дендрографа (рис.20). Он строится таким образом: по оси абсцисс располагаются исследуемые элементы и откладываются межгруппо­вые расстояния, по оси ординат откладываются значения d_Т

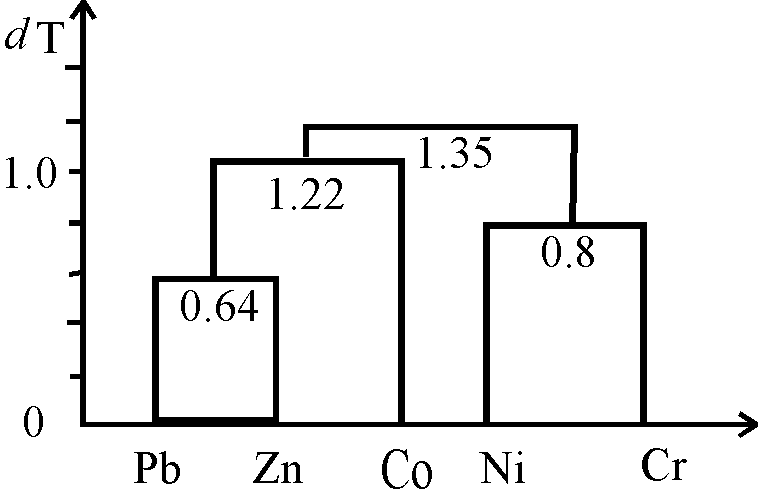
Рис.20. Дендрограф, построенный по данным табл. 11.

Для других метрик критические значения выбираются иначе, состав­лены специальные алгоритмы и программы. Однако в любом случае, предварительно необходим геологический анализ целесообразности деле­ния совокупности на определенное число групп. Только в том случае, если с геологических позиций нельзя сказать ничего определенного по этому поводу, порог группирования задается формальными методами.

2)Ранговый коэффициент корреляции, необходимость и границы его применения.

Коэффициент корреляции очень чувствителен к виду функции распределения величин, входящих в двумерную систему. Поэтому, если эти распределения отличаются от нормальных и не поддаются норма­лизации, для проверки гипотезы о наличии корреляционной связи следу­ет использовать ранговый коэффициент кор­реляции Спирмена. При этом каждому значению х и у присваи­вается ранг в порядке возрастания их значений. Если значения повто­ряются, им присваивается средний между повторяющимися значениями ранг. Выражение для r имеет вид:

r = 1 - , (51)

где n - количество пар значений в выборке, d - разность рангов со­пряженных значений х и у .

Для оценки значимости отличия рангового коэффициента корреляции от 0 существует специальная таблица критических значений (1, 16). Можно также воспользоваться выражением:

r _крит. =

где φ(р) - значение обратной функции нормального распределения при доверительной вероятности р (берется из таблицы).

Если вычисленное значение r окажется больше r _крит. , отличие его от нуля считается значимым. В противном случае считаем, что ли­нейная связь между величинами не установлена.

Пример.

Рассмотрим пример вычисления рангового коэффициента корреляции. Требуется определить наличие корреляционной связи между мощностью кварцевой жилы и содержанием в ней золота по данным опробования (таблица 6).

Вычисленное значение r равно:

r = 1- = 1-1.827 = -0.827

Критическое значение r, взятое из таблицы для уровня значимости 0,05 и числа наблюдений n=8, равно 0,738. Следовательно, считаем, что между мощностью жилы и содержанием в ней золота существует значимая отрицательная корреляционная связь.

Таблица 6.