2)Уравнения регрессии, методы вычисления их коэффициентов.

Соединив между собой множество условных центров распределения, мы получаем линию регрессии, которая является гра­фическим выражением формы связи между х и у. Урав­нение этой линии называется функцией или уравнением регрессии. Системе из 2-х величин всегда будет соответст­вовать две линии регрессии: у_х = f(х) и х_у = f(у). Регрессия может быть линейной (когда линии регрессии - прямые линии) и нели­нейной. Для линейной регрессии уравнения будут иметь следующий вид;

у =а₁ +в₁х (регрессия у на х );

х =а₂ +в₂у (регрессия х на у )

Линии регрессии пересекаются в точке, имеющей координаты и .

Коэффициенты уравнения регрессии могут быть получены непосред­ственно с графика (рис. 15). Угол γ характеризует при этом т е с н о т у связи между х и у . Чем меньше γ , тем ближе связь к функциональной.

Р

ис. 15. Графики уравнений линейной регрессии

в₁ = tg α; в₂ = tg β

Более точный, аналитический способ нахождения коэффициентов уравнения линейной регрессии из результатов опыта предложен Лежандром и Гауссом:

а₁ = , (43)

в₁ = , (44)

Билет №11

1)Дисперсионный анализ.

Обычной для геологии является ситуация, когда относительно имеющегося набора наблюдений заранее неизвестно, является ли он однородным или неоднородным и на какое число однородных групп его следует разделить. Поскольку статистическая неоднородность объекта означает его геологическую неоднородность, то ясно, что задача статистического разграничения совокупности наблюдений является ти­пичной при самых различных геохимических, петрографических, палеон­тологических и других исследованиях.

Задачи, основанные на проверке гипотезы о статистической однородности геологических объектов разделяются на 3 типа:

1) выделение аномальных значений;

2) разделение неоднородных выборочных совокупностей;

3) оценка степени влияния различных факторов на характер из­менчивости свойств объектов (дисперсионный анализ).

Оценка степени влияния различных факторов на характер из­менчивости свойств геологических объектов осуществляется с помощью дисперсионного анализа. Это статистический метод анализа, основанный на разложении общей дисперсии признака на составные части, обуслов­ленные влиянием различных факторов.

Это можно представить как:

( х - ) = α+ β + γ ,

где α - отклонение, вызываемое фактором A, β - отклонение, вызываемое фактором В, γ - отклонение, вызываемое другими неучтенными факторами. Иначе говоря, δ²_х = δ²_α + δ²_β + δ²_γ . Сравнивая δ²_α или δ²_β с δ²_γ можно установить степень влия­ния факторов А и В на величину х по сравнению с неучтенными факто­рами. Сравнивая δ²_α и δ²_β между собой, можно установить сравнительное влияние факторов А и В на х . Существенность влияния какого-либо фактора на исследуемую величину определяется по критерию Фишера:

F_А = ; F_В =

Если вычисленное значение превышает табличное, то влияние фактора признается значимым.

Пример.

Требуется выяснять, как влияют состав вмещающих пород (А) и гипсометрическое положение рудных тел (В) на среднее содержание в них золота. Данные по средним содержаниям приведены в таблице 5.

Таблица 5.

Содержание золота в рудных телах

А/В	Горизонт +800 м	Горизонт +500 м	Горизонт +200 м
Песчаники	1,0	2,0	3,0	2,0
Граниты	5,0	5,0	10,0	7,0
	3,0	4,0	6,5	4,5

S²_α = = = 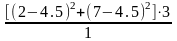37.5

S²_β= = = 6.5

S²_γ = = [(1-2-3+4.5)²+(2-2-4+4.5)²+(3-2-6.5+4.5)²⁺. . . +(10-7-6.5+4.5)²]/2 = 1.5

здесь n₁ - число столбцов, n₂ - число строк

F_а = =25 ; F_B = =4.3

Табличные значения для уровня значимости 0,05 и к₂ =2, к₁=1 равны: F_А = 18,5, F_В = 19,2. Таким образом, приходим к выводу, что влияние фактора А (состав вмещающих пород) на содержание золота в руде значимо, а влияние фактора В (гипсометрический уровень) - не­значимо.

По количеству исследуемых факторов дисперсионный анализ может быть одно-, двух- и многофакторным. При многофакторном анализе об­щая идея разложения дисперсии остается той же самой, но сложность вычислений резко возрастает. Например, для 4-факторного комплекса общая дисперсия разлагается уже на 14 составных частей.