Билет №1

1)Принципы и методы геолого-математического моделирования. Геологические совокупности: изучаемая, опробуемая, выборочная.

Необходимость применения моделей при описании природных объектов связана с тем, что геологические системы управляются одновременно многими факторами различной физической природы и не поддаются строгому количественному описанию.

В геологии моделируются не сами объекты, а изменчивость их свойств, наблюдаемая на данном уровне изучения объекта. Характер этой наблюдаемой изменчивости зависит не только от природы явления, но и от детальности геологических исследований и методики их проведения. В связи с этим необходимо рассмотреть понятие геологической совокупности.

Создание геолого-математической модели осуществляется в следующей последовательности:

1)Получение исходных данных об объекте или явлении путем измерения и определения его свойств.

2)Создание геологической модели объекта и формулировка геологической задачи.

3)Выражение поставленной задачи в математической форме. Создание математической модели. При этом может возникнуть необходимость в получении дополнительных данных или в уточнении геологических представлений об объекте.

4)Математические расчеты в соответствии с принятой моделью.

5)Проверка соответствия полученных результатов фактическим данным. Если геологических моделей было несколько (это обычный случай), можно оценить, какая из них лучше соответствует действительности.

Поскольку полученная модель учитывает лишь отдельные свойства объекта, ее можно последовательно усложнять и детализировать. Чем сложнее модель, тем более достоверно она отражает изучаемый объект и позволяет более надежно прогнозировать его свойства.

Степень сложности модели может также ограничиваться возможностями аналитических решений и электронно-вычислительной техники.

Под геологической совокупностью понимают множество геологических объектов, объединенных каким-либо признаком.

В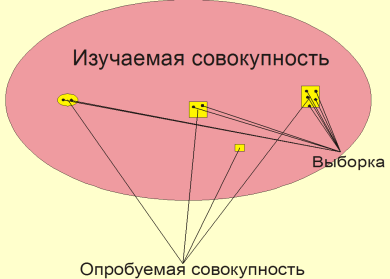 составе геологической совокупности выделяют изучаемую, опробуемую и выборочную совокупности.

Изучаемая совокупность – это геологическая совокупность в полном объеме.

Опробуемая совокупность - это совокупность с отдельными обнажениями (искусственными и естественными), характеризующими часть изучаемого объекта.

Выборочная совокупность – это совокупность образованная множеством всех произведенных над опробуемой совокупностью наблюдений.

2)Корреляционные связи между двумя величинами. Линии регрессии. Способы вычисления коэффициентов уравнения регрессии.

Форма и теснота корреля­ционной связи могут быть выражены аналитически, но обычно исследо­вание начинают не с расчетов, а с графического анализа зависимости в двухмерном пространстве. По оси абсцисс откладывают значения од­ного свойства, по оси ординат - другого. Совокупность наблюдений образует облако точек (рис. 14).

Рис.14. Облако точек, условные центры

Распределения и линия регрессии у на х.

Г

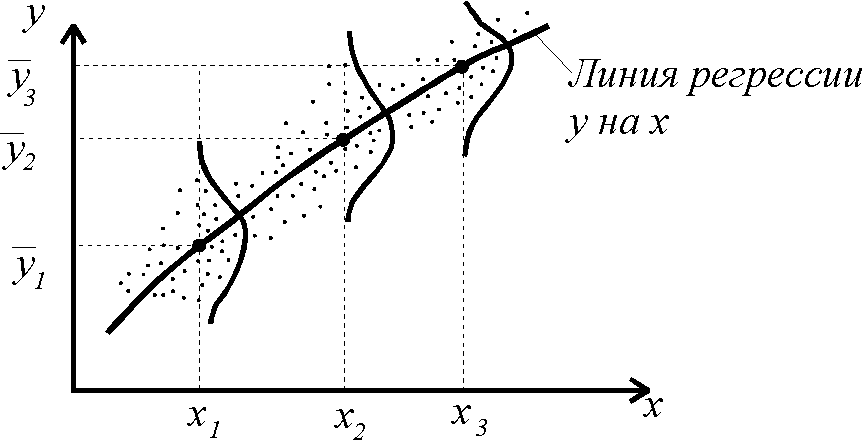
рафический анализ заключается в изучении формы и ориентировки облака точек. Если все точки располо­жены вдоль линии, то связь функциональная, если облако точек изометричное - связь отсутствует. Чаще облако точек вытянуто в виде эллип­са в каком-то направлении, характеризуя нестрогую корреляционную зависимость между свойствами.

Если мы возьмем на оси х произвольные точки х₁, х₂ , х₃, то каж­дой из них будут соответствовать наборы значений у со своими средними значениями 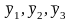(рис.14). Эти средние называются ус­ловными центрами распределения (среднее значение у равно 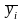при условии, что х = х_i ).

Соединив между собой множество условных центров распределения, мы получаем линию регрессии, которая является гра­фическим выражением формы связи между х и у. Урав­нение этой линии называется функцией или уравнением регрессии. Системе из 2-х величин всегда будет соответст­вовать две линии регрессии: у_х = f(х) и х_у = f(у). Регрессия может быть линейной (когда линии регрессии - прямые линии) и нели­нейной. Для линейной регрессии уравнения будут иметь следующий вид;

у =а₁ +в₁х (регрессия у на х );

х =а₂ +в₂у (регрессия х на у )

Линии регрессии пересекаются в точке, имеющей координаты 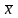и .

Коэффициенты уравнения регрессии могут быть получены непосред­ственно с графика (рис. 15). Угол γ характеризует при этом т е с н о т у связи между х и у . Чем меньше γ , тем ближе связь к функциональной.

Р

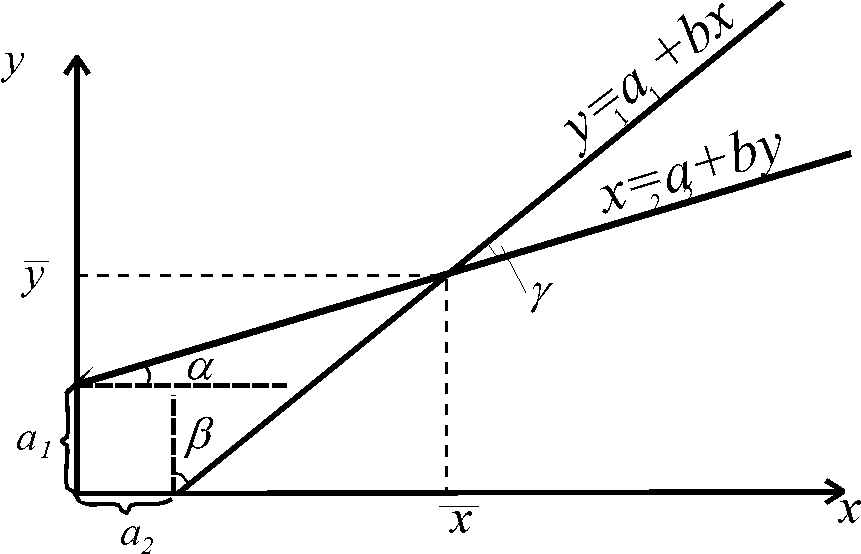
ис. 15. Графики уравнений линейной регрессии

в₁ = tg α; в₂ = tg β

Более точный, аналитический способ нахождения коэффициентов уравнения линейной регрессии из результатов опыта предложен Лежандром и Гауссом:

а₁ = , (43)

в₁ =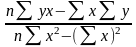 , (44)