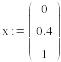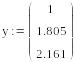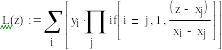- •Раздел 6.
- •Модели и алгоритмы решения задач численными методами с использованием математических пакетов Рекомендации по использованию лабораторного практикума
- •Тема 6.2. Лабораторная работа Методы решения нелинейных уравнений
- •1. Вопросы, подлежащие изучению
- •2. Задание
- •3. Варианты задания
- •4. Пример выполнения задания
- •Задание для решения нелинейных уравнений:
- •Отделение корней
- •«Ручной расчет» трех итераций методом половинного деления.
- •«Ручной расчет» трех итераций методом итераций
- •«Ручной расчет» трех итераций методом Ньютона
- •«Ручной расчет» трех итераций методом хорд
- •Уточним отделенный корень уравнения «расчетом средствами MathCad» с использованием функции root.
- •Тема 6.3. Лабораторная работа Интерполяция функций
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения задачи интерполяция функций
- •Результаты линейной интерполяция (узлы интерполяции z1 и z3), и квадратичной сплайн-интерполяция (узлы интерполяции z1, z2 и z3) и графики функций
- •Результаты интерполяция по формуле Лагранжа (узлы интерполяции z1, z2 и z3) и графики функций
- •Оценка погрешностей интерполяции функции f(X) в точках
- •Тема 6.4. Лабораторная работа Численное интегрирование
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для численного интегрирования:
- •Выражения первой и второй производной от заданной функции в символьном виде
- •Значение интеграла, полученное «расчетом средствами MathCad»
- •«Ручной расчет» определенного интеграла по заданному численному методу с шагом и ( и ) и оценка погрешности по правилу Рунге:
- •Оценка погрешности результатов интегрирования с шагом , приняв за точное значение интеграла величину
- •Тема 6.5. Лабораторная работа Методы решения обыкновенных дифференциальных уравнений
- •Вопросы, подлежащие изучению
- •Методы Рунге-Кутты различных порядков. Общие свойства. Погрешности методов.
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения оду:
- •Решение аналитическое (точное) заданного оду, найдем методом разделения переменных.
- •Решение оду «расчетом средствами MathCad»
- •Оценка погрешностей приближенных решений и их погрешности относительно точного (аналитического) решения
- •Графики решений оду, полученных с использованием аналитической формулы ( ) и приближенных методов Эйлера ( ) и Рунге-Кутта 4-го порядка ( ).
- •Тема 6.6. Лабораторная работа «Одномерная оптимизация»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения контрольного задания
- •Задание для решения задачи одномерной оптимизации:
- •Результаты исследования функции:
- •«Ручной расчет» трех итераций
- •Значение координат точки минимума функции y(X) «расчетом средствами MathCad» с использованием функций root, Minimize и Minеrr .
- •Тема 6.7. Лабораторная работа «Методы оптимизации функций нескольких переменных»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Тема 6.8. Лабораторная работа «Аппроксимация функций»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения задачи аппроксимации.
- •«Ручной расчет» коэффициентов линейной аппроксимирующей функции по методу наименьших квадратов и получение его аналитического выражения.
- •«Расчет средствами MathCad» для получения аналитических выражений линейной и квадратичной аппроксимирующих функций, и построение графиков точной и аппроксимирующих функций.
- •Литература
Пример выполнения задания
Задание для решения задачи интерполяция функций
№ узла-i |
0 |
1 |
2 |
3 |
4 |
5 |
xi |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
y=f(xi) |
1 |
1.411 |
1.805 |
2.113 |
2.256 |
2.161 |
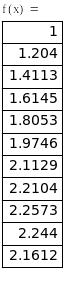
Таблица значений функции с шагом h=0.1 на [0;1] и точки z1, Z2 и z3
|
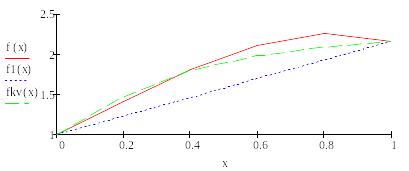
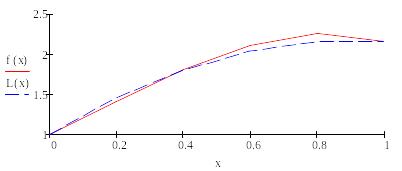
Результаты линейной интерполяция (узлы интерполяции z1 и z3), и квадратичной сплайн-интерполяция (узлы интерполяции z1, z2 и z3) и графики функций
Графики функций: f(x) - точная, f1(x) -линейная интерполяция, fkv(x) – квадратичная сплайн-интерполяция.
|
Результаты интерполяция по формуле Лагранжа (узлы интерполяции z1, z2 и z3) и графики функций
Интерполяционная формула Лагранжа
|
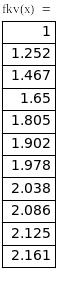
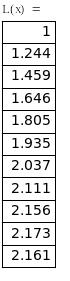
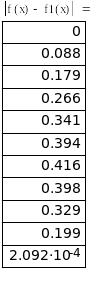
Оценка погрешностей интерполяции функции f(X) в точках
с шагом h=h/2
|
xi |
f(xi) |
fl(xi) |
fkv(xi) |
L(xi) |
|f(xi)- fl(xi)| |
|f(xi)- fkv(xi)| |
|f(xi)- L(xi)| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема 6.4. Лабораторная работа Численное интегрирование
Вопросы, подлежащие изучению
Постановка задачи численного интегрирования.
Методы численного интегрирования: прямоугольников, трапеций и Симпсона.
Оценка погрешности численного интегрирования. Правило Рунге.
«Расчет средствами MathCad» значений определенных интегралов от функции, заданной в аналитическом виде.
«Расчет средствами MathCad» производных первых и высших порядков от функций, заданных в аналитическом виде.
Получение символьного выражения для интегралов и производных путем «расчета средствами MathCad».
Реализации путем «расчета средствами MathCad»численных методов интегрирования:
метод средних прямоугольников
метод трапеций,
метод Симпсона
для случая таблично заданной подынтегральной функции.