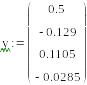- •Раздел 6.
- •Модели и алгоритмы решения задач численными методами с использованием математических пакетов Рекомендации по использованию лабораторного практикума
- •Тема 6.2. Лабораторная работа Методы решения нелинейных уравнений
- •1. Вопросы, подлежащие изучению
- •2. Задание
- •3. Варианты задания
- •4. Пример выполнения задания
- •Задание для решения нелинейных уравнений:
- •Отделение корней
- •«Ручной расчет» трех итераций методом половинного деления.
- •«Ручной расчет» трех итераций методом итераций
- •«Ручной расчет» трех итераций методом Ньютона
- •«Ручной расчет» трех итераций методом хорд
- •Уточним отделенный корень уравнения «расчетом средствами MathCad» с использованием функции root.
- •Тема 6.3. Лабораторная работа Интерполяция функций
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения задачи интерполяция функций
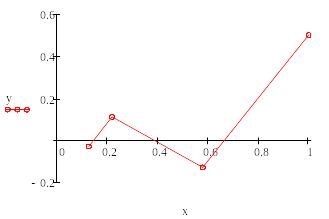
- •Результаты линейной интерполяция (узлы интерполяции z1 и z3), и квадратичной сплайн-интерполяция (узлы интерполяции z1, z2 и z3) и графики функций
- •Результаты интерполяция по формуле Лагранжа (узлы интерполяции z1, z2 и z3) и графики функций
- •Оценка погрешностей интерполяции функции f(X) в точках
- •Тема 6.4. Лабораторная работа Численное интегрирование
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для численного интегрирования:
- •Выражения первой и второй производной от заданной функции в символьном виде
- •Значение интеграла, полученное «расчетом средствами MathCad»
- •«Ручной расчет» определенного интеграла по заданному численному методу с шагом и ( и ) и оценка погрешности по правилу Рунге:
- •Оценка погрешности результатов интегрирования с шагом , приняв за точное значение интеграла величину
- •Тема 6.5. Лабораторная работа Методы решения обыкновенных дифференциальных уравнений
- •Вопросы, подлежащие изучению
- •Методы Рунге-Кутты различных порядков. Общие свойства. Погрешности методов.
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения оду:
- •Решение аналитическое (точное) заданного оду, найдем методом разделения переменных.
- •Решение оду «расчетом средствами MathCad»
- •Оценка погрешностей приближенных решений и их погрешности относительно точного (аналитического) решения
- •Графики решений оду, полученных с использованием аналитической формулы ( ) и приближенных методов Эйлера ( ) и Рунге-Кутта 4-го порядка ( ).
- •Тема 6.6. Лабораторная работа «Одномерная оптимизация»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения контрольного задания
- •Задание для решения задачи одномерной оптимизации:
- •Результаты исследования функции:
- •«Ручной расчет» трех итераций
- •Значение координат точки минимума функции y(X) «расчетом средствами MathCad» с использованием функций root, Minimize и Minеrr .
- •Тема 6.7. Лабораторная работа «Методы оптимизации функций нескольких переменных»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Тема 6.8. Лабораторная работа «Аппроксимация функций»
- •Вопросы, подлежащие изучению
- •Задание
- •Варианты задания
- •Пример выполнения задания
- •Задание для решения задачи аппроксимации.
- •«Ручной расчет» коэффициентов линейной аппроксимирующей функции по методу наименьших квадратов и получение его аналитического выражения.
- •«Расчет средствами MathCad» для получения аналитических выражений линейной и квадратичной аппроксимирующих функций, и построение графиков точной и аппроксимирующих функций.
- •Литература
Пример выполнения задания
Задание для вычисления точки минимума:
Функция
 .
.
Проверим существование минимума функции .
Проверим, что функция является выпуклой на множестве R.
Матрица Гессе для функции имеет следующий вид:
 .
.
Угловые миноры равны:

 .
.
Таким образом,
функция
 - выпуклая на множестве R.
- выпуклая на множестве R.
Найдем координаты точки минимума аналитическим методом.
Необходимые условия существования точки экстремума следующие:

 откуда
откуда

 .
.
Выберем начальную точку для решения задачи оптимизации методом наискорейшего спуска
 .
.
Решим задачу оптимизации аналитическим методом наискорейшего спуска.
Запишем рекуррентные формулы для получения значений координат очередной точки спуска:
 где;
где;


Построим функцию
 ,
,
Из условия
 определим параметр
определим параметр
 :
:
 ,
k=0, 1,…
,
k=0, 1,…
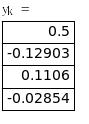
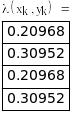
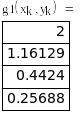
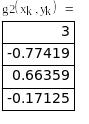
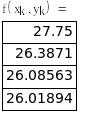
Используя рекуррентные формулы, выполним 3 итерации, а результаты вычислений сведем в таблицу:
|
xmin=0.1284, ymin=-0.0285, f(xmin,ymin)=26.0189.
Вычислим погрешности после трех итераций
|
Решение задачи оптимизации «расчетом средствами MathCad» с помощью функций Minimize и Мinerr:
использование функции Minimize
|
использование функции Мinerr
|
Трехмерный график функции f(x,y)
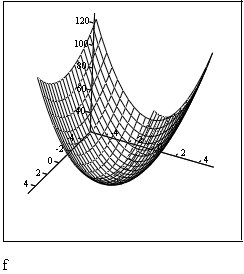
График линий уровня функции f(x,y)
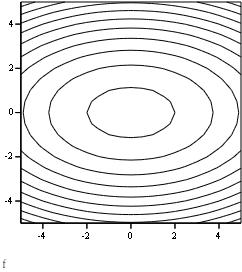
Траектория спуска, на основании данных ручного расчета.
Тема 6.8. Лабораторная работа «Аппроксимация функций»
Вопросы, подлежащие изучению
Постановка задачи аппроксимации.
Основные понятия: базисные функции, матрица Грама, система нормальных уравнений, критерий аппроксимации.
Метод наименьших квадратов.
«Расчет средствами MathCad» линейной и квадратичной аппроксимации с использованием функции linfit.
Задание
Выбрать индивидуальное задание:
номера узлов (xi, где i = 0, 1, …5) (табл. 6.8-1);
значения функции в заданных узлах (табл. 6.8-2) обозначим a = x0 и b = х5.
Провести «ручной расчет» коэффициентов линейной аппроксимирующей функции по методу наименьших квадратов и получить его аналитическое выражение.
Выполнить «расчет средствами MathCad» для получения аналитических выражений линейной и квадратичной аппроксимирующих функций, используя 6 точек таблицы исходной функции, построить графики точной и аппроксимирующих функций.
Получить таблицу значений аргумента и трех функций (точной и 2-х аппроксимирующих) на отрезке [a,b] (где
 )
и оценить
погрешности
линейной
и квадратичной аппроксимации
(невязки).
)
и оценить
погрешности
линейной
и квадратичной аппроксимации
(невязки).