
Занятие 2 Предельные теоремы в схеме Бернулли
Занятие
2 по
курсу «Теория вероятностей»
Формула
для вычисления биномиальнывероятностей
прекрасно работает, однако у нее есть
недостаток. Если число испытаний будет
достаточно большим, то найти соответствующую
вероятность становится практически
нереально из-за огромного объема
вычислений. В этом случае предельные
теоремы МуавраЛапласа
и Пуассона
позволяют найти приближенное значение
вероятности
Цели
занятия:
Сформировать
умения и навыки применения предельных
теорем в схеме Бернулли при решении
практических задач.
Развивать
познавательные возможности,
самостоятельность мышления. Воспитать
трудолюбие, активность.
04.03.2013
Симогин А.А.

Занятие 2. Предельные теоремы в схеме Бернулли
2.1. Основные факты и определения
При рассмотрении
числовых примеров при больших значениях
![]() и
и
![]() вычисление вероятностей
вычисление вероятностей
![]() превращается в технически сложную
задачу. Рассмотрим теоремы, которые
помогут нам преодолеть эту проблему,
предоставляя в руки приближенные формулы
для биномиальных вероятностей при
достаточно больших значениях
.
превращается в технически сложную
задачу. Рассмотрим теоремы, которые
помогут нам преодолеть эту проблему,
предоставляя в руки приближенные формулы
для биномиальных вероятностей при
достаточно больших значениях
.
|
Теорема 2.1.
(Локальная
предельная теорема Муавра-Лапласа)
Обозначим
в схеме Бернулли
где
|
Из этой теоремы
непосредственно следует приближенная
формула
![]() .
Данная аппроксимация наиболее хороша
при
.
Данная аппроксимация наиболее хороша
при
![]() .
Практически можно считать, что данная
замена дает хорошее приближение если
.
Практически можно считать, что данная
замена дает хорошее приближение если
![]() .
.
Функция
![]() называется функцией
Гаусса. Ее
значения табулированы, т.е. занесены в
таблицу, которая приведена практически
во всех учебниках и задачниках по теории
вероятностей, в частности ее значения
можно найти в приложении (Таблица 1).
называется функцией
Гаусса. Ее
значения табулированы, т.е. занесены в
таблицу, которая приведена практически
во всех учебниках и задачниках по теории
вероятностей, в частности ее значения
можно найти в приложении (Таблица 1).
При работе с таблицей значений функции Гаусса необходимо учитывать ее свойства:
![]() функция Гаусса
является четной;
функция Гаусса
является четной;
При больших
значениях
![]() имеем:
имеем:
![]() ,
т.е. при больших
,
практически при
,
т.е. при больших
,
практически при
![]() ,
,
![]() .
.
Пример 2.1. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик.
Решение.
Итак, по условию задачи
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то применима локальная предельная
теорема Муавра-Лапласа.
,
то применима локальная предельная
теорема Муавра-Лапласа.
Имеем
![]() ,
,
![]() ,
,
 ,
по таблице 1 находим
,
по таблице 1 находим
![]() ,
тогда искомая вероятность равна
,
тогда искомая вероятность равна

Ответ. 0,0797.
|
Теорема 2.2.
(Интегральная
предельная теорема Муавра-Лапласа)
Обозначим
в схеме Бернулли
,
,
.
Тогда если
при
и
,
где
произвольная постоянная, тогда при
|
Таким образом, справедлива приближенная формула
 ,
,
здесь
 .
.
Эта формула, также, дает приемлемое приближение при .
Функция
![]() не выражается в элементарных, но в
таблице 2 приложения приведена ее таблица
значений. При использовании данной
таблицы необходимо помнить свойства
функции
не выражается в элементарных, но в
таблице 2 приложения приведена ее таблица
значений. При использовании данной
таблицы необходимо помнить свойства
функции
При
 .
.
При больших (
 )
значения
практически равны 1.
)
значения
практически равны 1.При малых (
 )
значения
практически равны 0.
)
значения
практически равны 0.
Так же отметим,
что часто вместо функции
используют функцию Лапласа
 .
Ее свойства
.
Ее свойства
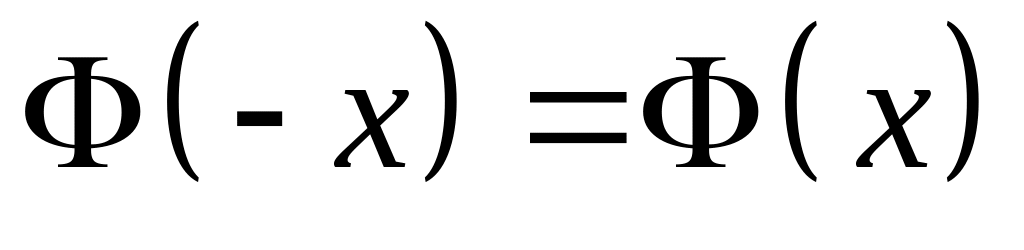 ,
функция Лапласа четная .
,
функция Лапласа четная .При
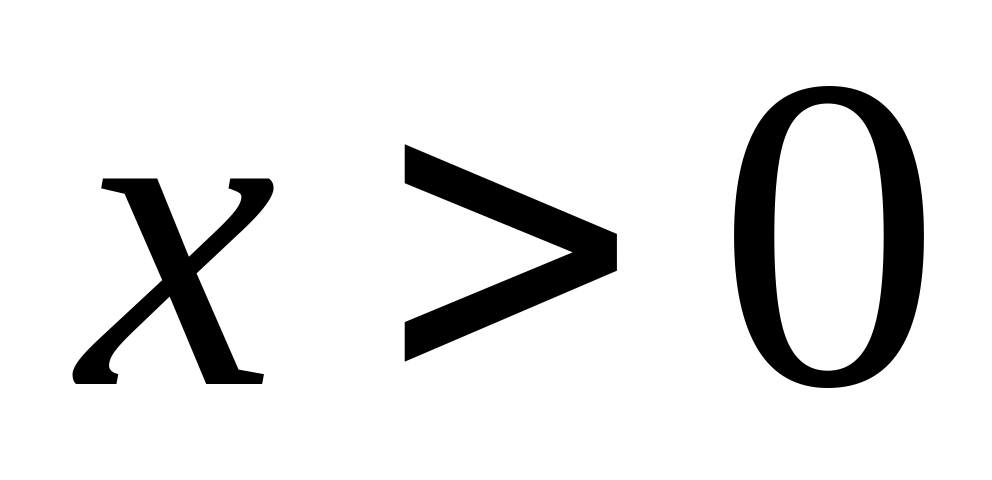 ,
,
 ,
связь между
и
,
связь между
и
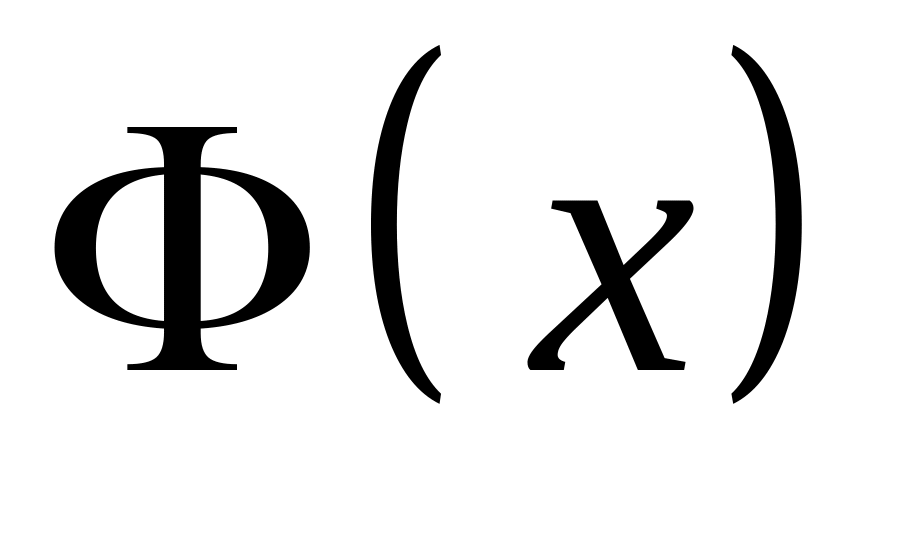 .
.
Пример 2.2. В продукции некоторого производства брак составляет 12%. Изделия отправляются потребителям (без проверки) в коробках по 200 штук. Найти вероятности событий:
а) А – наудачу взятая коробка содержит 20 бракованных изделий;
б) В – число бракованных изделий в коробке не превосходит 20.
Решение. В условиях
задачи
![]() ,
,
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то применимы предельные теоремы
Муавра-Лапласа. Вычислим
,
то применимы предельные теоремы
Муавра-Лапласа. Вычислим
![]() ,
,
![]() .
.
а) ![]()
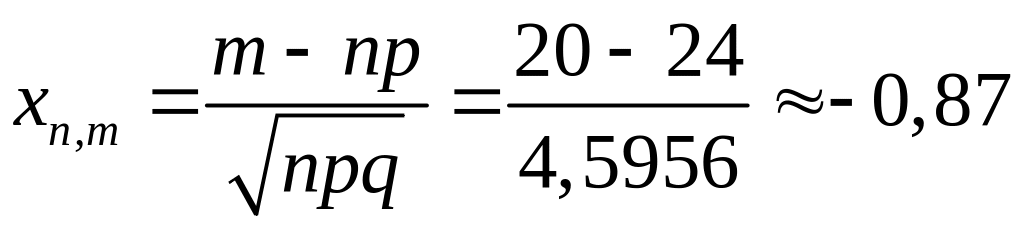 .
По таблице 1 находим
.
По таблице 1 находим
![]() .
Следовательно, согласно локальной
теореме искомая вероятность равна
.
Следовательно, согласно локальной
теореме искомая вероятность равна
 .
.
б) ![]()
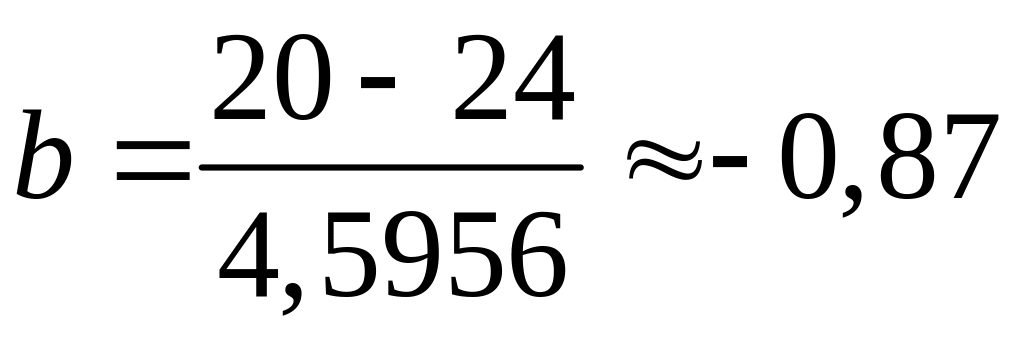 .
.
По таблице 2 находим
![]() .
Следовательно, по интегральной теореме
имеем
.
Следовательно, по интегральной теореме
имеем
![]() .
.
Ответ. а) 0,059, б) 0,1913.
Пример 2.3. Оценить близость частоты и вероятности в схеме Бернулли.
Решение. Пусть
![]() – вероятность успеха в схеме Бернулли
и
число успехов в
испытаниях. Частотой успеха называется
отношение
– вероятность успеха в схеме Бернулли
и
число успехов в
испытаниях. Частотой успеха называется
отношение
![]() .
.
Оценим вероятность
события
 .
Если
достаточно велико, то по интегральной
формуле Муавра-Лапласа имеем:
.
Если
достаточно велико, то по интегральной
формуле Муавра-Лапласа имеем:
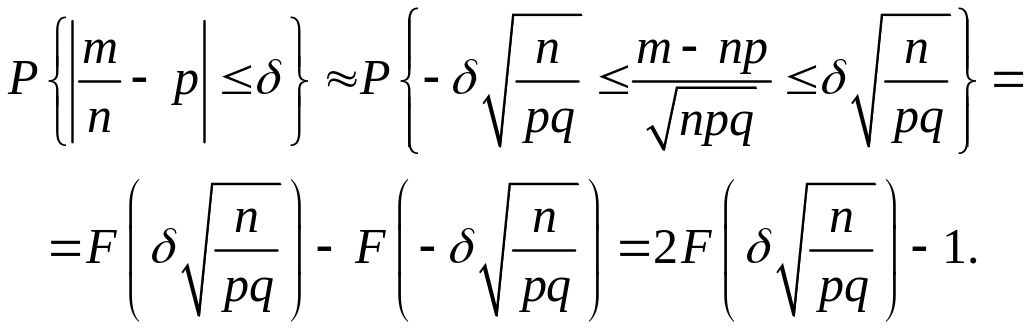
Часто возникает
обратная задача: сколько нужно провести
испытаний, чтобы частота
отличалась от вероятности
не больше, чем на
![]() с вероятностью
с вероятностью
![]() ?
?
Если считать известным, то из последнего равенства следует
 .
Решая его, получим, что наименьшее
определяется соотношением
.
Решая его, получим, что наименьшее
определяется соотношением
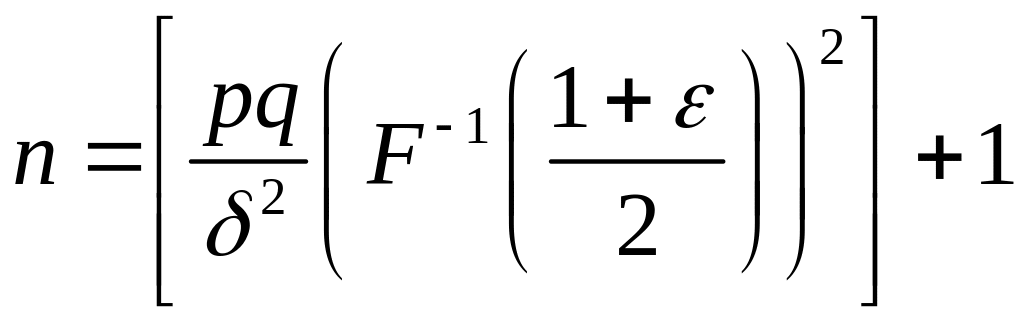 .
.
Часто в таких
задачах
является неизвестным. В этом случае
можно воспользоваться неравенством
![]() .
.
Тогда
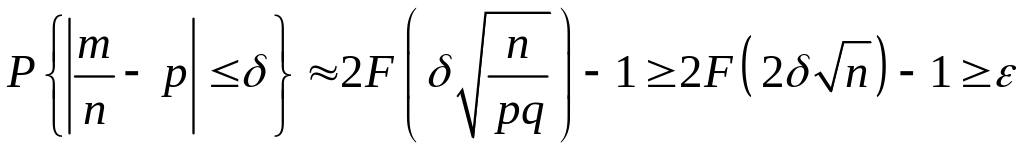 ,
,
или
 .
.
Пример 2.4. Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы c вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?
Решение.
Будем считать, что событие
![]() произошло, если турист пообедал у
заинтересованного владельца. По условию
задачи
произошло, если турист пообедал у
заинтересованного владельца. По условию
задачи
![]() ,
.
Нас интересует такое наименьшее число
посетителей
,
что вероятность одновременного прихода
не менее чем
туристов из числа
с вероятностью успеха
приблизительно равна вероятности
переполнения ресторана, т.е.
,
.
Нас интересует такое наименьшее число
посетителей
,
что вероятность одновременного прихода
не менее чем
туристов из числа
с вероятностью успеха
приблизительно равна вероятности
переполнения ресторана, т.е.
![]() .
.
Таким образом, нас
интересует такое наименьшее число
,
что
![]() .
Применим интегральную теорему
Муавра-Лапласа.
.
Применим интегральную теорему
Муавра-Лапласа.
В нашем случае:
– неизвестно,
![]() ,
,
![]()
![]() .
Тогда
.
Тогда
 или
или
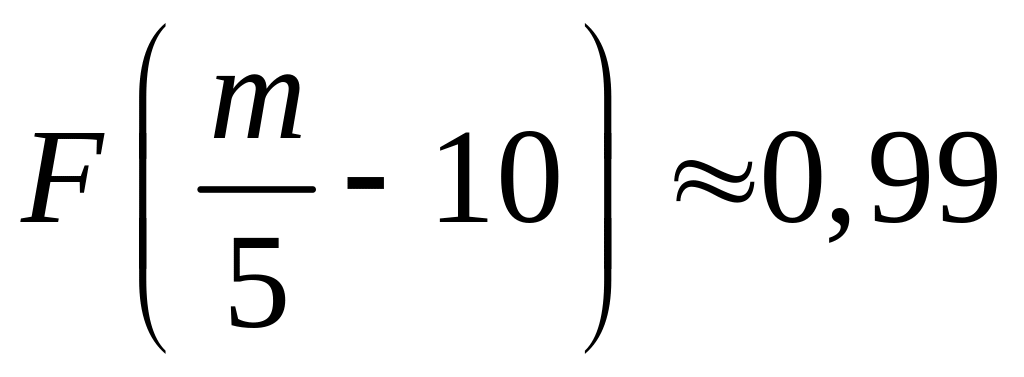 .
Используя таблицу 2 получим уравнение
.
Используя таблицу 2 получим уравнение
![]() ,
решая которое, получим
,
решая которое, получим
![]() .
Следовательно, в ресторане должно быть
62 места.
.
Следовательно, в ресторане должно быть
62 места.
Ответ. 62 места.
При большом числе испытаний и малой (большой) вероятности локальная теорема Муавра-Лапласа становится не применимой. В этом случае может помочь следующее утверждение.
|
Теорема 2.3.
(Теорема
Пуассона) Пусть
в схеме Бернулли
|
Формула
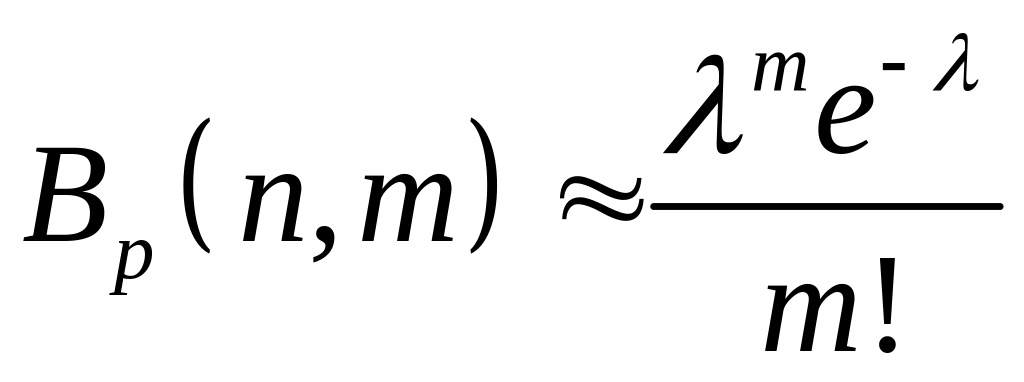 дает
удовлетворительное приближение для
дает
удовлетворительное приближение для ![]() и
и
![]()
![]() .
События, для которых применима формула
Пуассона, называют редкими, так как
вероятность их осуществления очень
мала.
.
События, для которых применима формула
Пуассона, называют редкими, так как
вероятность их осуществления очень
мала.
Пример 2.5. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов.
Решение
В условии задачи
,![]() ,
,
![]() .
Заметим, что
.
Заметим, что
![]() ,
поэтому следует пользоваться теоремой
Пуассона. В нашем случае
,
поэтому следует пользоваться теоремой
Пуассона. В нашем случае
![]() ,
следовательно
,
следовательно
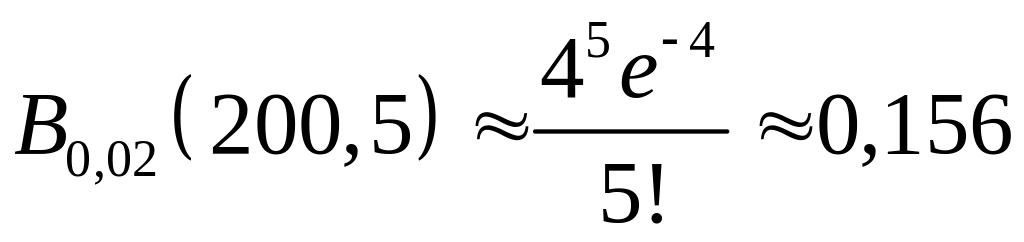 .
.
Ответ. 0,156.

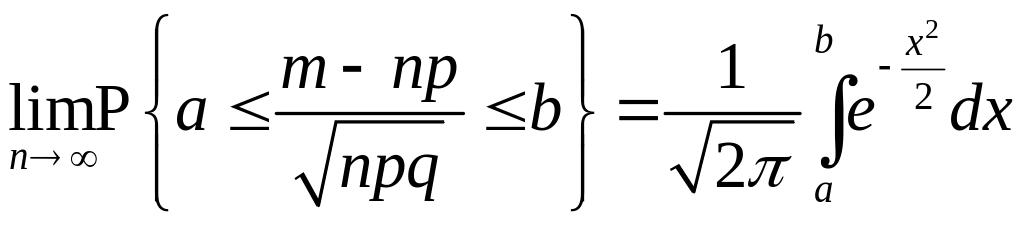 ,
,