1.3 Finite-Sample Properties of ols
Having
derived the OLS estimator, we now examine its finite-sample
properties, namely, the characteristics of the distribution of the
estimator that are valid for any given sample size
Finite-Sample Distribution of
Proposition 1.1 (finite-sample properties of the OLS estimator of ):
(unbiasedness) Under Assumptions 1.1-1.3,
(expression for the variance) Under Assumptions 1.1-1.4,
(Gauss-Markov Theorem) Under Assumptions 1.1-1.4, the OLS estimator is efficient in the class of linear unbiased estimators. That is, for any unbiased estimator
that is linear in
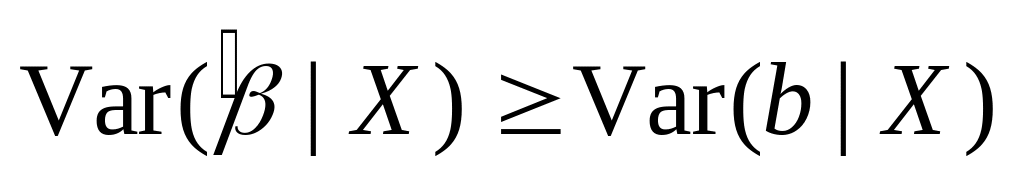in the matrix sense.13Under Assumptions 1.1-1.4,
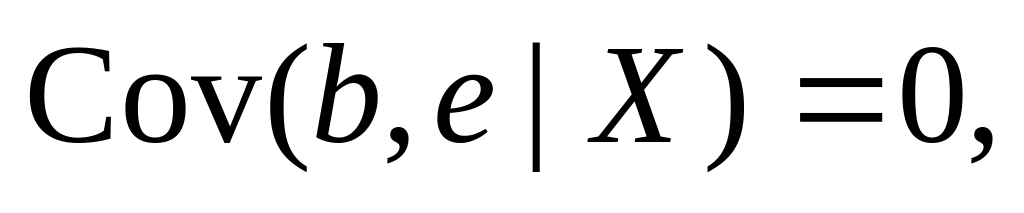where
Before plunging into the proof, let us be clear about what this proposition means.
• The
matrix inequality in part (c) says that the
matrix
is
positive semidefinite, so
for
any
-dimensional
vector
In particular, consider a special vector whose elements are all 0
except for the
-th
element, which is 1. For this particular
the quadratic form
picks
up the
element of
But
the
element of
for
example, is
where
is
the
-th
element of
Thus the matrix inequality in (c) implies
(1.3.1)
That is, for any regression coefficient, the variance of the OLS estimator is no larger than that of any other linear unbiased estimator.
As clear from (1.2.5), the OLS estimator is linear in
There
are many other estimators of
that are linear and unbiased (you will be asked to provide one in a
review question below). The Gauss-Markov Theorem says that the OLS
estimator is efficient
in
the sense that its conditional variance matrix
is
smallest among linear unbiased estimators. For this reason the OLS
estimator is called the Best Linear Unbiased Estimator (BLUE).
The OLS estimator is a function of the sample
Since
are
random, so is
Now imagine that we fix
at
some given value, calculate
for
all samples corresponding to all possible realizations of
and
take the average of
(the
Monte Carlo exercise to this chapter will ask you to do this). This
average is the (population) conditional mean
Part (a) (unbiasedness) says that this average equals the true value
There is another notion of unbiasedness that is weaker than the unbiasedness of part (a). By the Law of Total Expectations,
So (a) implies
(1.3.2)
This
says: if we calculated
for
all possible different samples, differing not only in
but also in
the
average would be the true value. This unconditional statement is
probably more relevant in economics because samples do differ in both
and
The import of the conditional statement (a) is that it implies the
unconditional statement (1.3.2), which is more relevant.
• The same holds for the conditional statement (c) about the variance. A review question below asks you to show that statements (a) and (b) imply
(1.3.3)
where
is
any linear unbiased estimator (so that
).
We will now go through the proof of this important result. The proof may look lengthy; if so, it is only because it records every step, however easy. In the first reading, you can skip the proof of part (c). Proof of (d) is a review question.
Proof.
(Proof that
)
whenever
So we prove the former. By the expression for the sampling error
(1.2.14),
where
here
is
So
Here,
the second equality holds by the linearity of conditional
expectations;
is
a function of
and
so can be treated as if nonrandom. Since
the last expression is zero.
(Proof that
)
(Gauss-Markov) Since is linear in it can be written as
for
some matrix
which possibly is a function of
Let
or
where
Then
Taking the conditional expectation of both sides, we obtain
Since
both
and
are
unbiased and since
it
follows
that
For this to be true for any given
it is necessary that
So
and
So
(since
both
and
are functions of
)
But
since
Also,
as shown in
(b). So
It
should be emphasized that the strict exogeneity assumption
(Assumption 1.2) is critical for proving unbiasedness. Anything short
of strict exogeneity will not do. For example, it is not enough to
assume that
for
all
or that
for
all
.
We noted in Section 1.1 that most time-series models do not satisfy
strict exogeneity even if they satisfy weaker conditions such as the
orthogonality condition
.
It follows that for those models the OLS estimator is not unbiased.
Finite-Sample Properties of
We defined the OLS estimator of in (1.2.13). It, too, is unbiased.
Proposition
1.2 (Unbiasedness of
):
Under
Assumptions 1.1-1.4,
(and hence
),
provided
(so
that
is
well-defined).
We can prove this proposition easily by the use of the trace operator.14
Proof.
Since
the proof amounts to showing that
As shown in (1.2.12),
where
is the annihilator. The proof consists of proving two properties: (1)
and (2)
(Proof that
)
Since
(this is just writing out the quadratic form
),
we
have
(since
for
by Assumption 1.4)
(2)
(Proof that
)
and
So
Estimate of
If
is
the estimate of
a
natural estimate of
is
(1.3.4)
This is one of the statistics included in the computer printout of any OLS software package.
QUESTIONS FOR REVIEW ___________________________________
1.
(Role
of the no-multicollinearity assumption) In Propositions 1.1 and 1.2,
where did we use Assumption 1.3 that
?
Hint:
We
need the no-multicollinearity condition to make sure
X'X is invertible.
(Example of a linear estimator) For the consumption function example in Example 1.1, propose a linear and unbiased estimator of that is different from the OLS estimator. Hint: How about
Is
it linear in
Is
it unbiased in the sense that
(What Gauss-Markov does not mean) Under Assumptions 1.1-1.4, does there exist a linear, but not necessarily unbiased, estimator of that has a variance smaller than that of the OLS estimator? If so, how small can the variance be? Hint: If an estimator of is a constant, then the estimator is trivially linear in
(Gauss-Markov for Unconditional Variance)
Prove:
Hint:
By
definition,
and
Use
the add-and-subtract strategy: take
and
add and subtract
Prove (1.3.3). Hint: If
then
Propose an unbiased estimator of if you had data on
Hint:
How
about
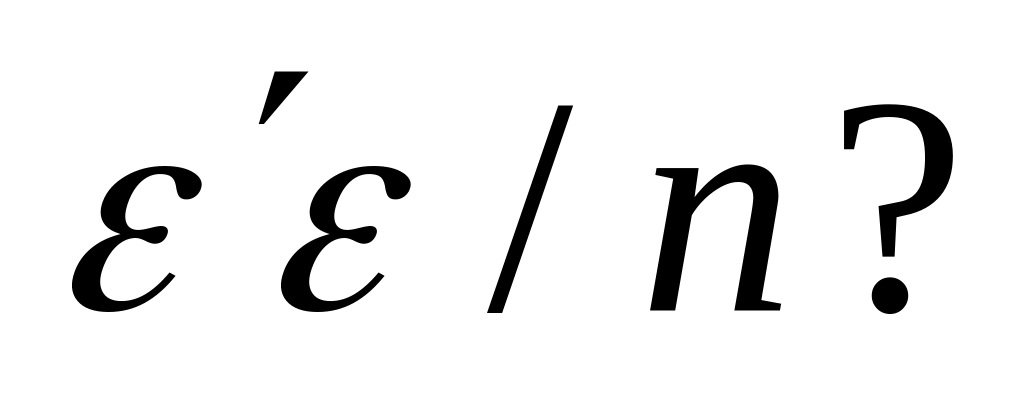Is it unbiased?Prove part (d) of Proposition 1.1. Hint: By definition,
Since
we
have
where
here
is
Use
(see Review Question 5 to Section 1.2) to show that
since
both
and
are
functions of
Finally,
use
(see
(1.2.11)).
Prove (1.2.21). Hint: Since is positive semidefinite, its diagonal elements are nonnegative. Note that
£n=1
pi
=
trace(P).