МІНІСТЕРСТВО ОСВІТИ І НАУКИ, молоді та спорту УКРАЇНИ

Технологічний коледж Національного університету

«Львівська політехніка»

Відділення комп’ютерних технологій

Інструкція до лабораторної роботи № 4 Дослідження базових логічних елементів

з дисципліни “Комп’ютерна електроніка”

Спеціальність 5.05010201 “Обслуговування комп’ютерних систем і мереж”

Напрям підготовки 6.050102 “Комп’ютерна інженерія”

ЛЬВІВ 2012

Інструкція до лабораторної роботи № 4 “Дослідження базових логічних елементів” з дисципліни "Комп’ютерна електроніка" для студентів коледжу спеціальності 5.05010201 “Обслуговування комп’ютерних систем і мереж” напряму підготовки 6.050102 “Комп’ютерна інженерія”- Львів: Видавництво Технологічного коледжу Національного університету «Львівська політехніка», 2012 - с. 12.

Укладач:

Викладач Технологічного коледжу Національного університету «Львівська політехніка» т.Д. Мандзевич

Інструкція до лабораторної роботи обговорена та схвалена на засіданні циклової комісії спеціальних комп’ютерних дисциплін коледжу

Протокол № від “____” __________2012 р.

Голова циклової комісії _______________ Л.М. Павліш

Рецензенти:

Войтович П.В. – викладач вищої категорії Технологічного коледжу Національного університету «Львівська політехніка»

Деревянченко Ю.Г. – викладач вищої категорії Технологічного коледжу Національного університету «Львівська політехніка»

Відповідальний за випуск:

Павліш Л.М. – голова циклової комісії спеціальних комп’ютерних дисциплін Технологічного коледжу Національного університету «Львівська політехніка»

© Мандзевич Т.Д., 2012

1. Мета роботи

Метою роботи є вивчення принципу дії та логіки роботи базових логічних елементів транзисторно-транзисторної логіки (БЛЕ ТТЛ), реалізація елементарних логічних операцій в базисі І-НЕ.

2. ТеоретичНа частина

Математичний апарат цифрової мікросхемотехніки.

Теоретичною основою проектування цифрових пристроїв є алгебра логіки. Розробка основ алгебри логіки пов'язана з іменем англійського математика Дж. Була (1815-1864), у зв'язку з чим ця алгебра називається також буловою алгеброю, або численням висловлень.

Під висловленням розуміють будь-яке твердження, про яке можна сказати, що воно істинне або хибне. В логіці висловлень не цікавляться змістом висловлень, а лише їх істинністю або хибністю. Якщо висловлення істинне, то вважають, що його значення дорівнює одиниці, якщо ж воно хибне, то його значення дорівнює нулеві. Отже, значення висловлень розглядають як змінну величину, яка може приймати лише два дискретні значення – 0 або 1. Як бачимо, існує відповідність між логічними висловленнями в алгебрі логіки та двійковими числами, що дозволяє описувати, аналізувати та синтезувати логічні схеми за допомогою математичного апарату алгебри логіки.

Логічні функції утворюються з логічних змінних, об'єднаних знаками логічних операцій. Як і логічні змінні, логічні функції можуть приймати лише значення "нуль" або "одиниця".

В кожному конкретному випадку кількість вхідних змінних логічної функції може бути різною. У найпростішому випадку це може бути лише одна змінна.

Різноманітні логічні функції можна утворювати за допомогою трьох основних логічних операцій або елементарних логічних функцій: логічного заперечення (інверсії), логічного множення (кон’юнкції) та логічного додавання (диз’юнкції).

Операція інверсії позначається горизонтальною рискою над відповідною змінною:

(1)

Вираз (1) означає, що коли x = 1, то y = 0, і навпаки, якщо x = 0, то y = 1. Іншими словами, можна сказати, що значення y – це не значення x. Тому інверсію часто називають операцією «НЕ».

Логічне множення (кон’юнкція) n змінних x₁, x₂,..., x_n – така логічна функція, яка приймає значення, що дорівнює одиниці лише в тому випадку, коли всі змінні одночасно дорівнюють одиниці. У всіх інших випадках значення функції дорівнює нулеві. Позначають кон'юнкцію знаком , який читають як «І», тому часто кон’юнкцію називають операцією «І»:

y = x₁  x₂ ... x_n (2)

Часто знак  опускають і записують y = x₁ x₂ ... x_n. Зауважимо, що у випадку n змінних можлива кількість різних комбінацій значень цих змінних дорівнює 2ⁿ.

Логічне додавання (диз'юнкція) n змінних x₁, x₂,..., x_n – така логічна функція, яка приймає значення, що дорівнює одиниці, якщо хоча б одна змінна дорівнює одиниці. Нулеві ця функція дорівнює лише тоді, коли всі змінні одночасно дорівнюють нулеві. Позначають диз'юнкцію знаком , який читають як «АБО», тому часто диз'юнкцію називають операцією «АБО»:

y = x₁  x₂ ... x_n (3)

Часто знак  заміняють знаком + і записують y = x₁ + x₂ + ... + x_n.

Аксіоми та теореми алгебри логіки

Для розглянутих раніше логічних операцій справедливий ряд ак­сіом та теорем, які наводяться нижче.

Аксіоми алгебри логіки.

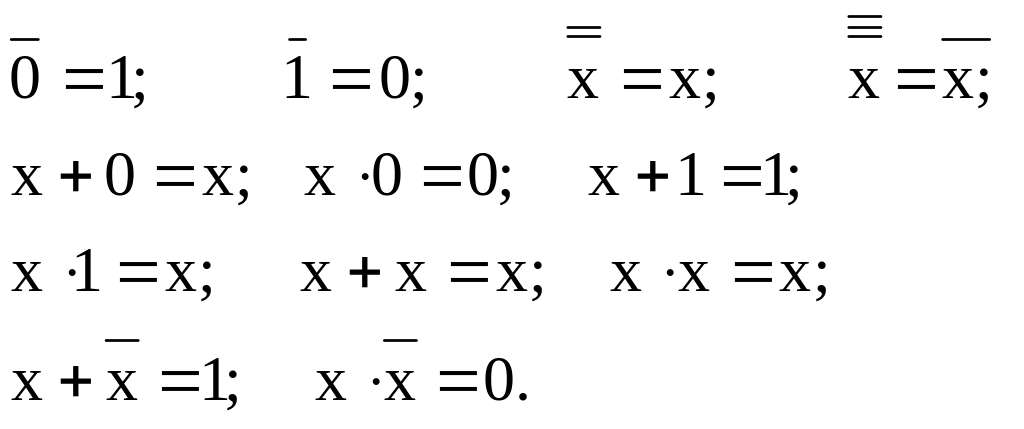
Закони алгебри логіки

Комутативний
Асоціативний
Дистрибутивний
Склеювання
Поглинання
де-Моргана

Наведені аксіоми та закони алгебри логіки дозволяють перевіряти справедливість тих чи інших логічних функцій, перетворювати та спрощувати їх.

Способи представлення логічних функцій

Відомі такі способи представлення логічних функцій: словесна, таблична, графічна та аналітична (алгебраїчна).

Табличною формою представлення логічної функції є таблиці істинності. Таблицею істинності називається таблиця, в якій записують всі можливі комбінації вхідних логічних змінних і значення логічної функції для кожної вхідної комбінації. Враховуючи, що із n логічних змінних x₁ ,x₂, ..., x_n можна утворити 2ⁿ різних комбінацій (вхідних наборів), таблиця істинності логічної функції y = f(x₁, x₂,…, x_n), буде мати 2ⁿ рядків та n+1 стовпець. Нижче наводимо таблиці істинності логічних функцій «НЕ» та «I», «АБО» для двох змінних (табл. 1).

Таблиця 1

Функція «НЕ»			Функція «І»				Функція «АБО»
x	y		x2	x1	y		x2	x1	y
0	1		0	0	0		0	0	0
1	0		0	1	0		0	1	1
-	-		1	0	0		1	0	1
-	-		1	1	1		1	1	1

Якщо логічна функція набуває конкретних значень (0 або 1) для кожної з вхідних комбінацій, то вона вважається повністю визначеною. У випадку, коли для деяких комбінацій функція не визначена, то вона називається частково визначеною.

Поняття про логічний базис та логічні елементи

Функціонально повним набором або логічним базисом називається набір логічних операцій, з допомогою яких можна утворити будь-яку логічну функцію. Прикладом такого набору є сукупність операцій диз'юнкції, кон'юнкції та інверсії.

Мінімальний логічний базис утворюють операції «І-НЕ» або «АБО-НЕ». Операція «І-НЕ» отримала назву штриха Шеффера а операція «АБО-НЕ» стрілки Пірса . Таблиці істинності логічних функцій «І-НЕ» та «АБО-НЕ» для двох змінних мають вигляд (табл. 2, 3):

Таблиця 2 Таблиця 3

Функція «І-НЕ»				Функція «АБО-НЕ»
х2	х1	у		х2	х1	у
0	0	1		0	0	1
0	1	1		0	1	0
1	0	1		1	0	0
1	1	0		1	1	0

Схеми, які реалізують одну з елементарних логічних операцій, називають логічними елементами (ЛЕ). Логічний елемент, який реалізує операцію диз'юнкції, називається диз'юнктором; операцію кон'юнкції - кон'юнктором; операцію інверсії - інвертором; операцію «АБО-НЕ» - елементом Пірса; операцію «І-НЕ» - елементом Шеффера.

Часові діаграми сигналів на входах та виходах найпростіших ЛЕ зображені на рис. 1, а їх схемні позначення наведені на рис. 2.

Реальні ЛЕ мають ряд особливостей, які відрізняють їх від ідеальних:

- кількість входів ЛЕ є обмеженою, що може призвести до необхідності додаткового перетворення синтезованих логічних функцій;

- навантажувальна здатність реальних ЛЕ скінченна, тобто до їх виходів можна під'єднувати обмежену кількість входів інших ЛЕ;

- кожний реальний ЛЕ характеризується певним часом затримки  передавання сигналу, що необхідно враховувати при проектуванні цифрових пристроїв.

Покажемо, що набором елементів І-НЕ (АБО-НЕ) можна реалізувати основні логічні функції НЕ, I, АБО. Цим буде доведено, що кожний такий набір являється мінімальним функціонально повним набором (мінімальним логічним базисом), так як базисом являється сукупність елементів НЕ, I, АБО. Для цього запишемо функцію, яку необхідно реалізувати і перетворимо її так, щоби у кінцевий результат входила кон’юнкція та інверсія (при використанні елементів І-НЕ) або диз’юнкція та інверсія (при використанні елементів АБО-НЕ) – табл.4.

Таблиця 4

Елемент	Логічні операції
	«НЕ»	«І»	«АБО»
«І-НЕ»
«АБО-НЕ»

При записуванні правих частин наведених функцій враховано:

для у₁ – тотожність х х... х = х, для у₄ – тотожність х + х+...+ х = х, для у₂ і у₆ – тотожність , для у₃ і у₅ – теорема де-Моргана. Отже, у відповідності з правою частиною наведених рівностей операції НЕ, I, АБО можуть бути виконані елементами І-НЕ, а також елементами АБО-НЕ (рис. 3).

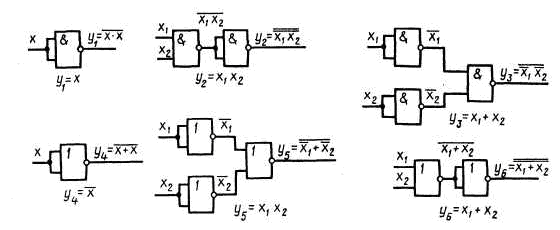
Рис. 3. Схемна реалізація основних логічних операцій

в базисах І-НЕ та АБО-НЕ

Логічні пристрої, реалізовані в мінімальному логічному базисі І-НЕ (АБО-НЕ), мають переваги у порівнянні з пристроями, реалізованими в базисі І, АБО, НЕ. Одна перевага заключається в зменшенні номенклатури елементів одного типу, що спрощує компоновку пристрою, його ремонт; інша пов’язана з наявністю в кожному елементі інвертора (підсилювача), який компенсує затухання потенціалів при передачі їх через кон’юнктор або диз’юнктор елемента. Завдяки цьому не нагромаджується затухання сигналу при його проходженні через ряд послідовно ввімкнених елементів, що могло б викликати зниження рівня U¹ (логічної 1) до рівня U⁰ (логічного 0). Крім того, інвертор збільшує навантажувальну здатність елемента: під’єднання допустимого числа інших елементів до його виходу не викликає помітного зменшення на ньому рівнів потенціалів (що особливо важливо для U¹), а наявність ємності навантаження на виході не викликає тривалого перехідного процесу при зміні потенціалів.