- •Содержание
- •Введение
- •1 Основная часть
- •1.1 Понятие математической модели. Виды моделей
- •1.2 Задача линейного программирования
- •1.3 Каноническая форма модели злп
- •1.4 Симплекс – метод решения злп
- •1.6 Решение злп в ms Excel
- •2 Практическая часть
- •2.1 Составление математической модели
- •2.2 Нахождение максимального дохода
- •2.3 Решение злп в ms Excel
- •Заключение
- •Список используемой литературы
- •Лист замечаний Рецензия преподавателя
2.2 Нахождение максимального дохода
Для решения задачи симплекс – методом приведем математическую модель к канонической форме:
f(x) =
9
+20
+15
+30
+0 +
0
+
0
 +
0
+
0
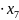 +
0
+
0
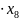 + 0
+ 0
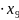 – M
– M
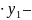 M
M
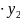 → max
→ max
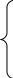 +
+
+
+
+
+
+
+
 = 50
= 50
+
2
+
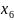 = 38
= 38
3
+
+
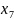 = 18
= 18
+ +
+
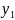 = 34
= 34
+
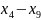 +
+
 =
6
=
6
≥ 0; i = 1÷9
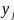 ≥ 0; j
= 1÷2
≥ 0; j
= 1÷2
На основании канонической формы построим начальный базисный план задачи (Таблица 2 – 6).
Таблица 2 - Итерация 0
базис |
1 |
0 |
9 |
20 |
15 |
30 |
0 |
0 |
С |
В |
|
|
|
|
|
|
|
|
0 |
50 |
1 |
1 |
1 |
1 |
0 |
0 |
|
0 |
38 |
1 |
2 |
0 |
0 |
0 |
0 |
|
0 |
18 |
0 |
0 |
3 |
1 |
0 |
0 |
|
M |
34 |
1 |
0 |
1 |
0 |
1 |
0 |
|
M |
6 |
0 |
1 |
0 |
1 |
0 |
1 |
|
∆i |
40М |
М 9 |
М 20 |
М 15 |
М 30 |
М |
М |
f(x) = ( 1 0) + (0 50) + (0 38) + (0 18) + ( М 34) + ( М 6) = 40М
∆1 = ( 1 9) + (0 1) + (0 1) + (0 0) + ( М 1) + ( М 0) = М 9
∆2 = ( 1 20) + (0 1) + (0 2) + (0 0) + ( М 0) + ( М 1) = М 20
∆3 = ( 1 15) + (0 1) + (0 0) + (0 3) + ( М 1) + ( М 0) = М 15
∆4 = ( 1 30) + (0 1) + (0 0) + (0 1) + ( М 0) + ( М 1) = М 30
∆5 = ( 1 0) + (0 0) + (0 0) + (0 0) + ( М 1) + ( М 0) = М
∆6
= (
1
0) + (0
0) + (0
0) + (0
0) + (
М
 )
+ (
М
1)
= М
)
+ (
М
1)
= М
Задача не решена, так как в базисе имеются искусственные переменные и в целевой функции относительные оценки отрицательны. Переходим к следующей итерации.
Таблица 3 – Итерация 1
-
базис
1
0
9
20
15
0
0
С
В
0
44
1
0
1
0
0
0
38
1
2
0
0
0
0
12
0
1
3
0
0
М
34
1
0
1
1
0
30
6
0
1
0
0
1
∆i
34М+180
М 9
10
М 15
М
30
Целевая функция и относительные оценки рассчитываются так же, как и в Итерации 0. Задача не решена, так как в базисе имеются искусственные переменные и в целевой функции относительные оценки отрицательные. Переходим к следующей итерации.
Таблица 4 – Итерация 2
-
базис
1
0
9
20
0
0
0
С
В
0
40
1
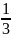

0
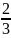
0
38
1
2
0
0
0
15
4
0
0
М
30
1
1
30
6
0
1
0
0
-1
∆i
30M+240
M 9


M
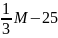
Целевая функция и относительные оценки рассчитываются так же, как и в Итерации 0. Задача не решена, так как в базисе имеются искусственные переменные и в целевой функции относительные оценки отрицательные. Переходим к следующей итерации.
Таблица 5 – Итерация 3
-
базис
1
0
20
0
0
0
С
В
0
10
0
0
1
1
0
8
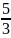
1
15
4
0
9
30
1
30
6
1
0
0
1
∆i
510
8
2
9
28
Целевая функция и относительные оценки рассчитываются так же, как и в Итерации 0. Задача не решена, в целевой функции относительные оценки отрицательные. Переходим к следующей итерации.
Таблица 6 – Итерация 4
-
базис
1
0
20
0
0
0
С
В
0
10
0
0
1
1
0
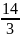
15
9
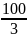
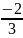
30
16
1
0
1
1
∆i
790
8
2
19
28
Целевая функция и относительные оценки рассчитываются так же, как и в Итерации 0. Задача решена, в базисе нет искусственных переменных и в целевой функции нет отрицательных относительных оценок.
Таким образом 33 изделия вида И1 изготовила бригада Б1 и 16 изделий вида И2 изготовила бригада Б2.