1.4 Симплекс – метод решения злп

Графический метод решения на плоскости x₁ 0 x₂ идеально подходит для решения ЗЛП с двумя переменными. Его можно применять и для решения задач с тремя переменными, но уже с большими трудностями построения.

Для решения задач, у которых количество переменных более трех, этот метод уже не применим. По этому для решения задач такой сложности разработаны специальные методы решения, одним из которых является симплекс-метод, или метод последовательного улучшения плана.

Графический метод более наглядный, симплекс-метод не обладает наглядностью, им можно решать ЗЛП с любым количеством переменных.

Известно, что оптимальные решения ЗЛП связана с угловыми точками многогранника решений.

Количество угловых точек (при n>2), называемых крайними равно количеству ограничений в ММ задачи.

Количество угловых точек равно количеству базисных решений, при чем для каждого базисного решения однозначно определяется значение целевой функции.

При решении задач на max целевая функция возрастает, на min – убывает. Уменьшение или возрастание значения целевой функции при поиске extr при беспорядочном переборе всех базисных решений может происходить не монотонно.

Необходим такой переход от одного базисного решения к другому, в результате которого в невырожденных задачах целевая функция монотонно возрастает или монотонно убывает.

Симплекс-метод решения ЗЛП реализует именно такой процесс решения, которые продолжается до получения оптимального решения или до установления факта его отсутствия.

Если ЗЛП вырожденное, то при переходе от одного базисного решения удругому значение целевой функции может не изменяться. Переход от одного базисного решения к другому называется итерацией симплекс-метода.

Критерии разрешимости ЗЛП.

Для того чтобы задача линейного программирования имела оптимальное решение необходимо и достаточно:

1. Чтобы ограничение задачи были совместимы

2. Целевая функция должна быть ограничена при поиске max сверху, при поиске min снизу.

Симплекс-метод геометрически может быть интерпретирован как движение по соседним угловым точкам многогранника решений.

Для решения ЗЛП симплекс-методом применяют симплекс-таблицы. ММ задачи приводят к канонической форме, на основании которой заполняют исходную симплекс-таблицу, таблица 1.

f(x) = → max

=

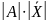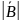
x_i≥ 0; 0 ≥ i ≤ n+m

Таблица 1 - Общий вид симплекс-таблицы

Базис	-1	0	С1	С2	…..	Сn
	С	В	X1	X2	…..	Xn
Xn+1	0	b1	a11	a21	…..	a1n
Xn+2	0	b2	a21	a22	…..	a2n
…..	…..	…..	…..	…..	…..	…..
Xn+m	0	bm	an+m,1	an+m,2	…..	an+m,n
	∆i	f(x)	∆1	∆i	…..	∆n

Значение целевой функции f(x) вычисляется как сумма парных произведений элементов С и В. Числа ∆i называются относительными оценками и вычисляются как сумма парных произведений элементов столбца С и столбца соответствующего выбранной перемененной x_i.

Алгоритм решения ЗЛП симплекс-методом

1. Привести ММ к канонической форме. Заполнить по ней симплекс-таблицу и найти значение целевой функции и относительных оценок.

2. Если все относительные оценки не отрицательные и среди базисных переменных нет искусственных, то план оптимален и решением являются значения находящиеся в столбце В.

x_n+1 = b₁

…..

x_n+m= b_m

Если все относительные оценки не отрицательные и среди них есть равные нулю, а в базисе нет искусственных, то задача имеет множество решений, одно из которых вышло в базис В.

Если все относительные оценки не отрицательные и в базисе остались искусственные переменные, то решений нет.

Если среди относительных оценок имеются отрицательные, то данный план не оптимален и необходим переход к следующему базисному плану.

3. Из всех отрицательных относительных оценок выбирается наибольшее по модулю. Столбец соответствующий ей называется главным. Для нахождения главной строки надо поэлементно разделить столбец В на главный столбец (на 0 и отрицательные элементы главного столбца не делят). Из получившихся частных выбираем наименьшее, которое соответствует главной строке. На пересечении главного столбца и главной строки лежит главный элемент симплекс-таблицы – он только положительный. Далее необходимо произвести перерасчет таблицы.

4. В новой таблице переменные главной строки и главного столбца меняются местами, коэффициенты при них также меняются местами, остальные переменные и их коэффициенты переписываются без изменений.

Вместо главного элемента записывается обратное ему число.

Элементы главного столбца старой таблицы делят на ( главнй элемент) и результат записывают в новую таблицу.

Элементы главной строки старой таблицы делят на главный элемент и результат записывают в новую таблицу.

Все остальные элементы пересчитывают по правилу прямоугольника: из произведения элементов главной диагонали проходящей через главный элемент, вычитают произведение побочной диагонали, делят эту разницу на главный элемент и записывают результат в соответствующую клетку новой симплекс-таблицы.

Если в главной строке или главном столбце есть нуль, то элементы соответствующих этим нулям столбца и строки переписываются без изменения в новую таблицу.

5. В новой таблице вычисляют значения целевой функции и относительных оценок.

1.5 М – метод решения ЗЛП

Все перемененные в математической модели делятся на:

1. Базисные переменные, которые могут быть выражены через все остальные. Переменная называется базисной, если она входит только в одно из уравнений системы ограничений, при чем с коэффициентом равным единице.

2. Все остальные переменные не базисные.

Частное решение, то есть нахождение базисных переменных при приравнивании не базисных переменных к нулю (x_i = 0), называется базисным. Базисное решение называется вырожденным, если хотя бы одна из базисных переменных равна 0, в противном случае задача считается невырожденной.

В первом случае базисное решение является x_n+1 = b₁ … x_n+m = b_m

x_n+1 = b₁ … x_n+m = b_m – это не допустимое решение, т.к. противоречит условию не отрицательности переменных.

По этому дл выделения базисных переменных и нахождения допустимого решения в подобных случаях используют метод искусственного базиса заключающийся в следующем:

1. Каждое ограничение вида ≥ или = вводят искусственную неотрицательную переменную y₁ … y_n.

2. В целевую функцию искусственные входят с коэффициентом ( М), где М – очень большое положительное число.

После ввода искусственных переменных задача f(x) = c₁x₁ + c₂x₂ + …+ c_nx_n → min

a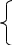 ₁₁x₁ + a₁₂x₂ + … + a_1nx_n b₁

…..

a_m1x₁ + a_m2x₂ + … + a_mnx_n ≥ b_m

x_i≥ 0; i =1 n

b_j ≥ 0; j =1 m будет иметь окончательный вид КФ:

f(x) = (c₁x₁ + … + c_nx_n) + 0 x_n+1 + 0 x_n+2 + … + 0 x_n+m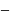 M y₁ … M y_m → max

a ₁₁x₁ + a₁₂x₂ + … + a_1nx_n x_n+1 + y₁= b₁

…..

a_m1x₁ + a_m2x₂ + … + a_mnx_n x_n+m+ y_m= b_m

x_i≥ 0; i =1 m+n

b_j ≥ 0; y_j ≥ 0; j =1 m

MM КФ

≤ + x_n+1 = b₁

≥ x_n+1 + y₁ = b₂

= + y₂ = b₃

Набор искусственных переменных y₁ … y_m в М-методе образует искусственный базис. Искусственные переменные вводятся только для получения исходного базисного плана при решении ЗЛП симплекс-методом. В ходе решения задачи они друг за другом должны выходить из базиса.