10.4 Анализ связи между атрибутивными признаками

Использование регрессионного и корреляционного анализа требует, чтобы все признаки были количественно измеренными. Методы КРА, основанные на использовании количественных параметров распределения (средние величины, дисперсия), называют параметрическими методами.

Вместе с тем в статистике, особенно при проведении социологических исследований, возникает потребность оценки тесноты связи между качественными (атрибутивными) признаками. Проблему оценки тесноты связи между атрибутивными признаками решают непараметрические методы. Сфера их использования значительно шире в сравнении с параметрическими методами, потому что не требует использования условия нормального распределения результативной переменной, не ставится задача представления зависимости между атрибутивными признаками соответствующим уравнением. Здесь речь идет только о наличии установления связи и измерения его тесноты.

Взаимосвязь между атрибутивными признаками анализируется посредством таблиц взаимной сопряженности. Они описывают комбинационные распределения совокупности по факторному признаку х и результативному у.

Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.

Занятия родителей	Число детей, занятых в				Всего
	промышлен- ности и стро- ительстве	сельском хозяйстве	сфере обслужи- вания	сфере интел- лектуального труда
1. Промышленность и строительство	40	5	7	39	91
2. Сельское хозяйство	34	29	13	12	88
3. Сфера обслуживания	16	6	15	19	56
4. Сфера интеллектульного труда	24	5	9	72	110
Всего	114	45	44	142	345

Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.

Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.

Однако важно получить обобщающие показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях.

При наличии стохастической связи оценка ее тесноты базируется на отклонениях фактических частот f_ij от F_ij, пропорциональных итоговым частотам:

,

где f_i0-суммарные частоты по признаку х; f_0j - суммарные частоты по признаку у; n – объем совокупности.

Абсолютную величину отклонений фактических частот f_ij от пропорциональных F_ij (f_ij - F_ij) характеризуют статистическим критерием .

.

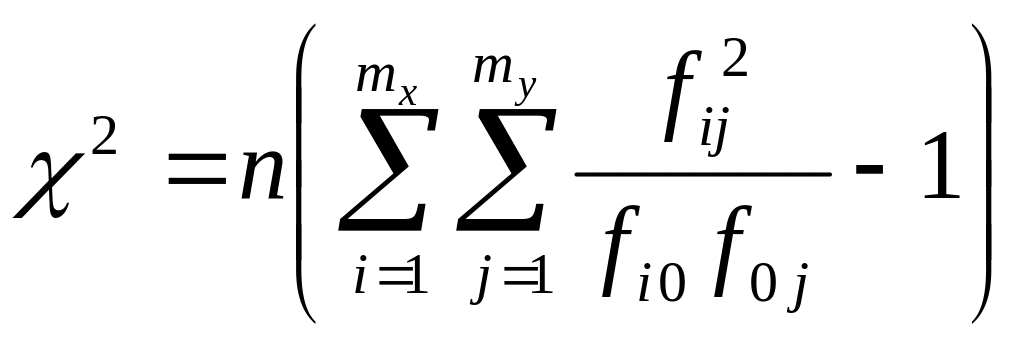При отсутствии стохастической связи =0. Для вывода о тесноте связи теоретическое значение сравнивают с табличным и делают вывод о наличии тесной связи между признаками х и у.

Относительной мерой тесноты стохастической связи между признаками служат также:

- коэффициент взаимной сопряженности Чупрова

;

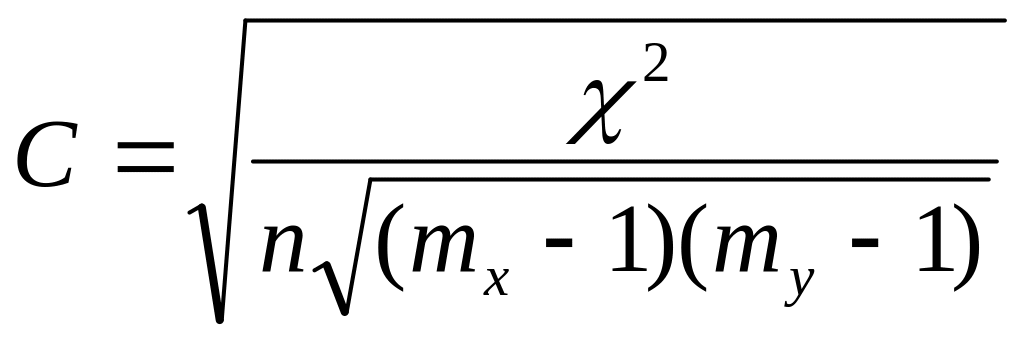- коэффициент взаимной сопряженности Крамера (при m_x m_y).

,

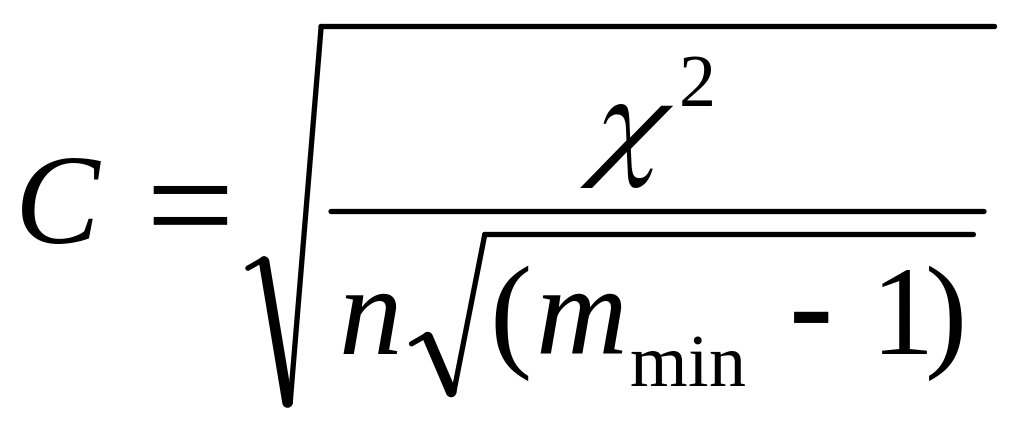где m_min – минимальное число групп (m_x или m_y).

Значение коэффициент С колеблется от 0 до 1 и теснота связи тем сильнее, чем более близко С к 1.

Достаточно часто в практике статистических исследований анализируются связи между альтернативными признаками, которые представлены группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценивать посредством коэффициента ассоциации Д.Юла и коэффициента контингенции К.Пирсона.

Для расчета указанных коэффициентов измерения тесноты связи между альтернативными признаками используется таблица взаимной сопряженности в виде корреляционной таблицы, которая носит название «четырехклеточной таблицы».

Таблица 10.1 - Таблица взаимной сопряженности

a	b	a+d
c	d	c+d
a+c	b+d	a+b+c+d

При использовании таблицы 10.1 с частотами a,b,c,d коэффициент ассоциации (К_а) вычисляется по формуле:

При К_а>0,3 между изучаемыми качественными признаками существует корреляционная связь.

В случаях, когда один из показателей четерехклеточной таблицы отсутствует, величина коэффициента ассоциации будет равняться единице, что дает завышенную оценку тесноты связи между признаками. В этом случае необходимо рассчитывать коэффициент контингенции (К_k):

Коэффициент контингенции находится в диапазоне от -1 к +1. Чем более близок K_k к (+1) или (-1), тем теснее связь между изучаемыми признаками. Коэффициент контингенции всегда меньше коэффициента ассоциации.

Для определения связи как между количественными, так и между качественными признаками при условии, что значения этих признаков упорядочены по степени уменьшения или увеличения (ранжированные), может быть использован коэффициент корреляции рангов Спирмена. Рангами называют числа натурального ряда, которые представляются в баллах по определенным критериям элементов совокупности. При этом ранжирование проводится по каждому признаку отдельно: первый ранг предоставляется наименьшему значению признака, последний – наибольшему. Количество рангов равняется объему совокупности. Преимуществом этого подхода является то, что при отсутствии требования нормального распределения ранговые оценки тесноты связи целесообразно использовать для совокупности небольшого объема.

Показатель ранговой корреляции – коэффициент корреляции рангов Спирмена – рассчитывается по формуле:

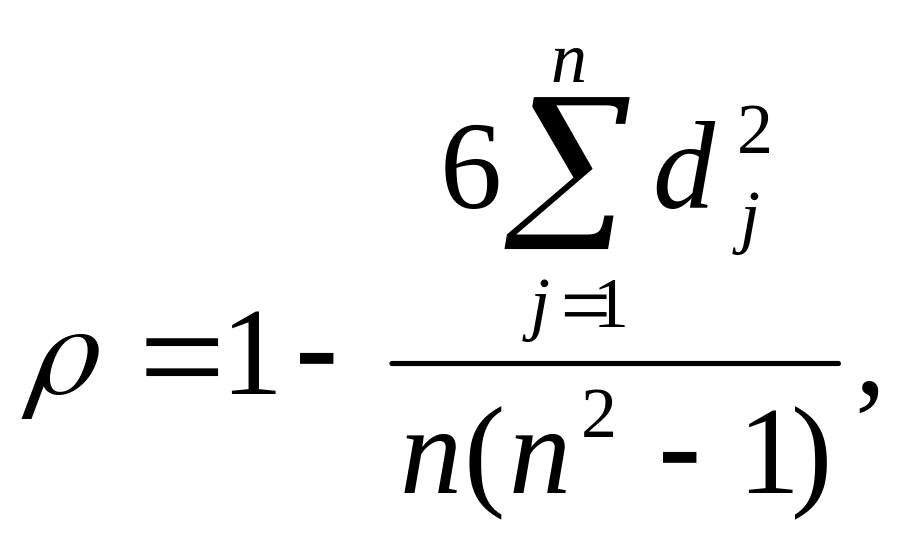
где - разность между рангами по одному и другому признаку ( );

n – количество единиц в ряду.

Если =0, то - существует тесная прямая связь. Если первому рангу по размеру одного признака соответствует последний ранг по размеру второго признака, второму рангу – предпоследний ранг второго признака и т.п., то и существует тесная обратная связь. Если значение близко к нулю, то связь слабая или ее вообще нет.

Упражнения и задачи

Задача 10.1

Рассчитайте параметры линейного уравнения парной регрессии, которое будет характеризовать зависимость между недельным розничным товарооборотом (д.е.) на душу населения и доходами населения (д.е.), и проведите анализ параметров регрессии по данным таблицы 10.1.

Таблица 10.1 – Исходные данные

Доходы населения	18	20	21	22	24	25	27	28	29	31
Розничный товарооборот	17	18	19	20	21	23	24	25	26	27

Задача 10.2

По данным задачи 10.1 оцените тесноту и значимость связи между признаками. Сделайте выводы.

Задача 10.3

Оцените тесноту связи между атрибутивными признаками рабочих предприятия по данным таблицы 10.2.

Таблица 10.2 – Распределение мнений по оценке содержания работы

Работа	Мужчины	Женщины	Итого
Интересная	300 (а)	200 (b)	500 (a + b)
Неинтересная	129 (с)	251 (d)	380 (c + d)
Всего	429 (а + с)	451 (b + d)	880 ( a + b + c + d)

Задача 10.4

Требуется доказать, влияет ли увеличение дозы внесения минеральных удобрений на урожайность зерновых культур.

Результаты опыта приведены в таблице 10.3.

Таблица 10.3 – Результаты опыта

Варианты опыта по внесению удобрений, ц/га	Урожайность по повторностям, Y1
	I	II	III	IV	V	VI	гр
Контроль	18	18	14	17	19	16	17
1,5	15	21	18	19	19	16	18
2,0	22	20	19	19	23	17	20
2,5	20	25	19	21	23	18	21

Задача 10.5

20 явлений сгруппированы в четыре группы по 5 явлений в каждой группе. Общая сумма квадратов отклонений от общей средней равны 160. Средние значения изучаемого признака по группам равны: 17, 20, 21, 18. С помощью дисперсионного метода доказать, что различия между средними по группам не случайные, а вызваны влиянием изучаемого фактора. Табличное значение F-критерия с вероятностью p=0,95 равно F_табл=3,5.

Задача 10.6

По следующим данным (табл. 10.4) с помощью критерия при 5% уровне значимости проверьте гипотезу о том, что «наследственность» является фактором возникновения гипертонической болезни.

Оцените тесноту связи между заболеваемостью и наследственностью с помощью:

С – коэффициента взаимной сопряжённости Пирсона;

С’– нормированного коэффициента Пирсона;

Т – коэффициента взаимной сопряжённости Чупрова.

Таблица 10.4 – Исходные данные

Родители больны гипертонией	Обследовано на заводе «Электосигнал», чел.
	Всего	Больные гипертонией	Здоровые
Да	17	15	2
Нет	73	30	43
Итого	90	45	45

Задача 10.7

По ряду районов Закарпатья определены: среднесуточное количество йода в воде и пище и пораженность населения заболеванием щитовидной железы.

Номер района	Количество йода в воде и пище (усл.ед.)	Пораженность населения заболеванием щитовидной железы, %
1	201	0,2
2	178	0,6
3	155	1,1
4	154	0,8
5	126	2,5
6	81	4,4
7	71	16,9

Для оценки тесноты связи пораженности заболеванием щитовидной железы с количеством йода в воде и пище определите коэффициенты корреляции рангов Спирмена, Кэнделла и Фехнера.

Контрольные вопросы

1. Почему возникает необходимость в установлении связи между признаками явлений?

2. Какие признаки называются факторными, результативными?

3. Какую связь между признаками называют функциональной? Приведите примеры?

4. Какую связь между признаками называют стохастической? Приведите примеры.

5. Какую связь между признаками называют корреляционной? Приведите примеры.

6. Что представляет собой уравнение регрессии?

7. Что представляет собой корреляционно-регрессионный анализ?

8. Суть регрессионного анализа.

9. Какие уравнения регрессии называют парными, а какие множественными?

10. Суть корреляционного анализа.

11. Какие виды уравнений парной регрессии наиболее распространены при характеристике социально-экономических явлений? Какие линии регрессии они описывают?

12. Приведите примеры использования линейной, параболической, гиперболической, степенной зависимости парной регрессии. Объясните структуру и вид зависимости.

13. Объясните понятие тесноты и значимости связи между признаками.

14. Характеристики тесноты связи: коэффициент детерминации; коэффициент корреляции.

15. Статистические критерии значимости связи между признаками: F-критерий Фишера; t-критерий Стьюдента.

16. Как оценивается теснота связи между атрибутивными признаками?