Практическая работа №1 вариация признаков качества и её измерения

Цель: ознакомится с основными методами статистического контроля качества, научится практически определять качество процессов, при помощи оценки основных статистических характеристик.

Вопросы для обсуждения:

1. Что такое «статистические методы и инструменты»?

2. Каковы области применения статистических методов в управлении качеством продукции?

3. Какие статистические методы контроля и анализа вы знаете?

4. Расскажите об основных этапах сбора данных при заполнении контрольного листка.

5. Какие символы используют при заполнении контрольных листков?

Темы докладов:

1. Основные этапы развития методов статистического контроля качества.

2. Ведущие специалисты в области управления качеством в Украине.

3. Основные теории в области управления качеством за рубежом.

Вопросы для самостоятельной работы:

1. Дайте основные определения понятия «качество» и «управление качеством»

2. Затраты на качество

3. Методы определения затрат на оценку и управление качеством.

4. Статистические методы при оценке качества продукции.

5. Что такое контрольный листок и для чего он предназначен?

6. Какие виды контрольных листков вы знаете?

1. Теоретические данные

Чрезвычайно важной характеристикой любого явления или процесса является его вариация. Вариация это природное рассеивание индивидуальных значений признака. Вариация существует во всех явлениях и процессах. Она возникает из-за действия многочисленных причин, которые либо усиливают, либо уменьшают вариацию, от нее невозможно избавиться, поскольку вариабельность является внутренней составляющей всего существующего, но ее возможно оценивать и контролировать путем осуществления определенных действий. Вариация находит •свое проявление лишь в массовых явлениях, и поэтому изучается статистикой, как наукою о массовых явлениях и процессах. Вариация признаков, которые изучаются является одним из основных статистических понятий и играет чрезвычайно большую роль в характеристике объекта исследования. В статистике существует ряд показателей, посредством которых возможно предоставить количественного выражения мере вариации определенного признака. Эти показатели обобщают отклонение индивидуальных значений от среднего значения исследуемой характеристики, то есть являются средними из индивидуальных отклонений.

Самым простым показателем, который характеризует вариацию признаков имеется размах вариации (R), который представляет собой разницу между максимальным и минимальным значением признака:

Он показывает, в каких границах варьирует признак. Но как мера вариации этот показатель не всегда надежен, поскольку зависит от случайных колебаний крайних значений признака.

Более точную характеристику меры вариации может давать показатель который учитывает все индивидуальные отклонения . Поскольку , при расчете среднего отклонения необходимо избавиться от знаков отклонения. Для этого необходимо взять либо абсолютные (без учета знаков) отклонения, либо возвести отклонение в квадрат.

Средняя из абсолютных отклонений называется средним линейным отклонением (d), которое, аналогично средним величинам, бывает простым и взвешенным. Простое среднее линейное отклонение используется в тех случаях, когда расчет ведется по не сгруппированным данным:

Среднее линейное отклонение взвешенное используется в тех случаях, когда данные, по которым ведется расчет, сгруппированные:

где f - частота повторяемости признака.

Средняя из квадратов отклонений называется дисперсией ( ) и рассчитывается по следующей формулой:

простая

взвешенная

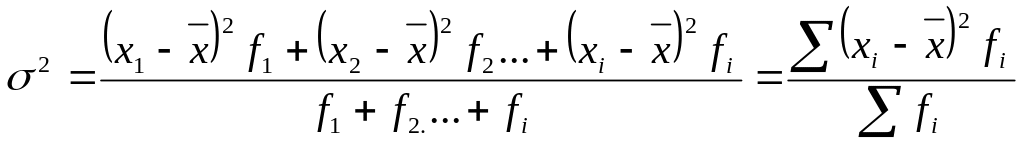
Для того, чтобы дать характеристику вариации в тех же единицах измерения, что и исследуемый признак, нужно из дисперсии добыть квадратный корень. Полученный в результате показатель имеет название средне­го квадратичного отклонения и рассчитывается как:

Среднее квадратичное отклонение (взвешенное):

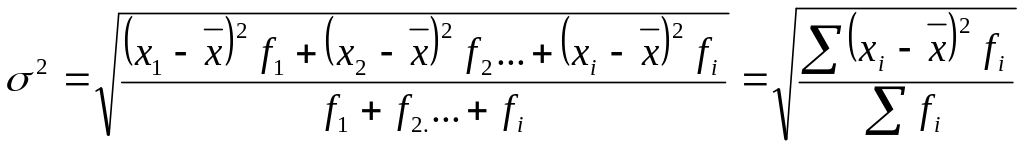
Среднее квадратичное отклонение еще имеет название стандартное отклонение и показывает, на сколько единиц в среднем индивидуальные значения признаки отклоняются от среднего значения. Дальше оба термина будем использовать как синонимы.

Если нужно определить меру вариации не в единицах измерения признака качества, а в процентах к среднему значению, тогда используем показатель, который имеет название коэффициент вариации, и который определяется по формуле:

или:

Коэффициент вариации показывает, на сколько процентов в среднем индивидуальные значения признака отличаются от среднего значения признака.

Для альтернативного признака, когда р - часть элементов с определенным признаком в совокупности, дисперсия определяется как:

Действительно, если пометим р = 1, а , - частота, которая отвечает части р, тогда средняя альтернативного признака будет равняться:

Средний квадрат отклонений определяется по обычной формуле:

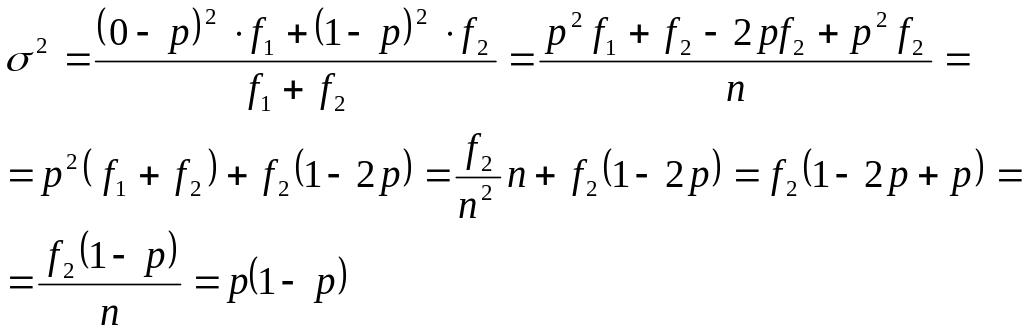
Пример 1. Производитель батарей формата АА исследует время работы батарей. Проведено 10 намерений длительности работы, результаты которых приведено ниже (в часах):

Таблица 1

Результаты измерений длительности работы батареек

№	1	2	3	4	5	6	7	8	9	10
Время работы	25,5	26,8	24,2	25,0	27,3	26,1	23,2	28,4	27,8	25,7

Руководству нужно знать вариацию времени работы батарей.

Решение. По этим данным размах вариации составляет:

Для нахождения среднего квадратичного отклонения сначала нужно определить среднее время работы:

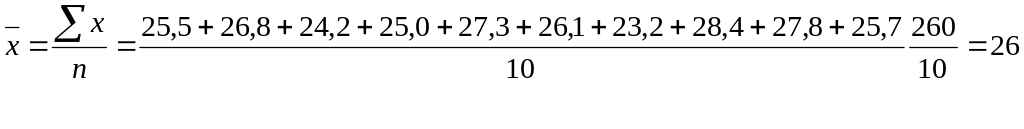
Дальше определяем среднее квадратичное отклонение:

Таблица 2

Расчеты для определения вариации длительности работы батарей

№ з/п
1	25,5	-0,50	0,25
2	26,8	0,80	0,64
3	24,2	-1,80	3,24
4	25,0	-1,00	1,00
5	27,3	1,30	1,69
6	26,1	0,10	0,01
7	23,2	-2,80	7,84
8	28,4	2,40	5,76
9	27,8	1,80	3,24
10	25,7	-0,30	0,09
Всего		-	23,76

Подставив сумму квадратов отклонений индивидуальных значений признака от средней величины в формулу среднего квадратичного отклонения, получим:

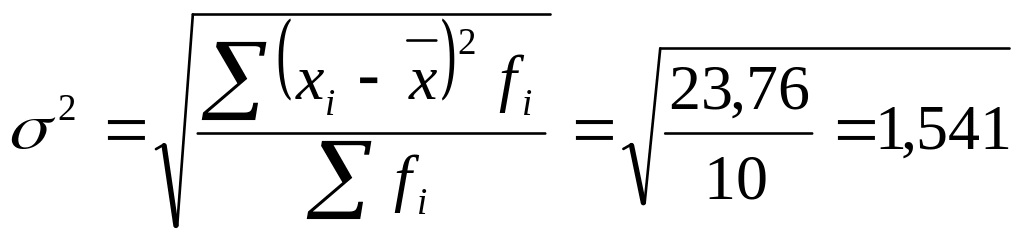
Следовательно, в среднем время работы батареи отличается от среднего времени работы в 26 часов на 1,54 часа.

Пример 2. На предприятии было проведенный исследование содержания определенного вещества в конечном продукте в зависимости от температурных режимов обработки. Нужно определить, при каком температурном ре­жиме содержание вещества в продукте является более стойким. Результаты наблюдений приведены в табл. 2.

Таблица 3

Содержание вещества (%) при разных температурных режимах

Температурный режим (град.)	Наблюдения
	1	2	3	4	5	6
125	2,7	2,6	4,6	3,2	3,0	3,8
160	4,6	4,9	5,0	4,2	3,6	4,2
200	4,6	2,9	3,4	3,5	4,1	5,1

Содержание вещества в продукте будет более стойким для того темпера­турного режима, у которого среднее квадратичное отклонение или коэффициент вариации является наименьшим, поскольку стабильность, то есть отсутствие, отклонений это понятие противоположное вариабельности.

Следовательно, нам нужно определить коэффициенты вариации для каждого температурного режима обработки и осуществить их сравнение. Средние значения будут следующие:

Дальше для каждого температурного режима найдем соответствующее среднеквадратическое отклонение. Для большего удобства расчеты лучше выполнять в таблицах, а в формулу подставлять лишь суммы.

Следовательно, имеем следующее:

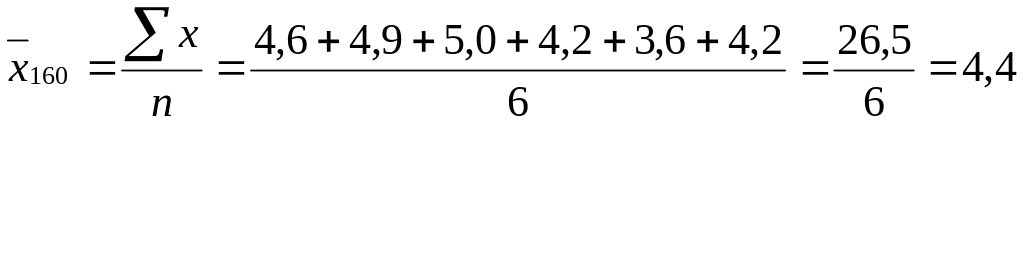
Таблица 3

Исходные данные		Расчетные показатели
№ исследования	Состав вещества %
1	2,7	-0,62	0,3844
2	2,6	-0,72	0,5184
3	4,6	1,28	1,6384
4	3,2	-0,12	0,0144
5	3,0	-0,32	0,1024
6	3,8	0,48	0,2304
Всего	-	-	2,8884

Таблица 4

№ исследования	Состав вещества %
1	4,6	0,18	0,03
2	4,9	0,48	0,23
3	5	0,58	0,34
4	4,22	-0,22	0,05
5	3,6	-0,82	0,67
6	4,2	-0,22	0,05
Всего	26,52	-	1,37

Таблица 5

№ исследования	Состав вещества %
1	4,6	0,67	0,44
2	2,9	-1,03	1,07
3	3,4	-0,53	0,28
4	3,5	-0,43	0,19
5	4,1	0,17	0,03
6	5,1	1,17	1,36
Всего	23,6	-	3,37

Следовательно, наибольшее среднее квадратичное отклонение имеет температурный режим в 200 градусов, а менее всего -у 160.

Таким образом, именно при этом режиме содержание вещества является наиболее стойким.

Пример 3. По результатам проверки изготовленных деталей на предприятии получены следующие результаты:

Таблица 6

Результата наблюдений размера изготовленных деталей

№ исследования	Размер изделия, мм.	Количество деталей, шт.
1	10,000 – 10,004	8
2	10,005-10,009	12
3	10,010 -10,014	7
4	10,015 – 10,020	3

Нужно определить среднее квадратичное отклонение размера деталей.

Решение. Поскольку каждая варианта представлена в виде интервалов, определим серединные варианты. Каждая варианта встречается определенное число раз, поэтому используем взвешенную формулу для определения среднего квадратичного отклонения:

Таблица 7

Исходные данные			Расчетные показатели
№ исследования	Размер изделий, мм.	Количество деталей, шт.
1	10,002	8	-0,00583	0,000034	0,000272
2	10,007	12	-0,00083	0,000001	0,000008
3	10,012	7	0,004167	0,000017	0,000122
4	10,017	3	0,009167	0,00084	0,000252
Всего		30		0,000136	0,000654

Используя результаты расчетов, приведенные в таблице 7 имеем: