83

4. Введення в математичний аналіз

Математичний аналіз (аналіз нескінченно малих) вивчає функції і їх узагальнення методом нескінченно малих величин.

У природі і техніці усюди спостерігаються рухи і процеси, що є проявом взаємодії між фізичними тілами або середовищами. Математичною моделлю рухів (тобто змінних величин) є функції, які виражають зміни одних величин зі зміною інших. Звідси слідує важливість математичного аналізу в прикладній математиці.

Основними розділами математичного аналізу є: диференціальне і інтегральне числення.

4.1. Дійсні числа

Поняття дійсних чисел було розглянуте раннє в розділі "Узагальнення поняття величини".

Сукупність раціональних і ірраціональних чисел утворює множину дійсних чисел.

Ірраціональні числа представляються нескінченним неперіодичним десятковим дробом. Наприклад, числа =1,414213., π = 3,141592., е = 2,718281. - є ірраціональними числами.

В той час, як раціональні числа, тобто числа виду представляються нескінченним періодичним десятковим дробом. Наприклад, 2 = 2,(0) = 1,(9), 1/3 = 0,(3), 13/7 = 1,(857142).

Множина дійсних чисел або числова пряма позначаються як R = { r }. Відмітимо деякі властивості цієї нескінченної множини чисел.

Передусім, R усюди щільно і утворює числовий континуум. Числова пряма R "подібна" до геометричної прямої, тобто між числами з R і точками на прямій можна встановити взаємно однозначну відповідність зі збереженням впорядкованості. Найважливішою властивістю числової прямої є її безперервність. Саме ця безперервність лежить в основі математичного аналізу і складає основу теорії границь.

Відмітимо також і іншу особливість числової множини R, яка взагалі характерна для багатьох нескінченних множин. Розглянемо поняття потужності нескінченної множини R , це поняття еквівалентно поняттю кількості членів кінцевої множини. Потужності нескінченних множин можуть бути різними, наприклад, множина натуральних чисел N, яка є підмножиною дійсних чисел (N R) має потужність рахункової множини, тоді як R має потужність континуальної множини. Покажемо, що потужність числового відрізку від нуля до одиниці має таку ж потужність, як і уся пів нескінченна числова пряма (від нуля до плюс нескінченність), тобто частина по потужності дорівнює цілому. Проведемо наступні міркування. Виділимо на пів нескінченній числовій осі одиничний відрізок. Поставимо у взаємно однозначну відповідність точки одиничного відрізку ОА з точками пів нескінченної прямої, таким чином (див. рис 4.1) :

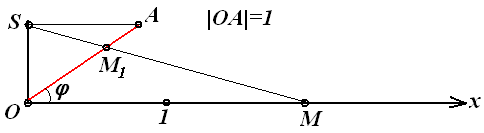
Рис.4.1.

• початковій точці О піввісі Ox побудуємо одиничний відрізок OA під деяким кутом φ до півосі;

• проведемо перпендикуляр до числової осі з точки О;

• з кінця А одиничного відрізку OA проводиться лінія паралельна числовій осі;

• точку перетину цієї лінії з перпендикуляром позначимо як S і назвемо її проектором;

• проводиться промінь (довільним чином) з проектора S на числову піввісь. Він перетинає одиничний відрізок в точці М₁, а піввісь Ox в точці М .

Таким чином, встановлена взаємно-однозначна відповідність між точками одиничного відрізку ОА і точками півосі Ох. Кожній точці М₁ відрізку ОА за допомогою променя проектора відповідає точка М осі х, і навпаки. Точці О відрізу відповідає точка О вісі, а точка А відрізка відповідає нескінченно видалена точка осі. Отже потужність числової множині півосі дорівнює потужності числової підмножині одиничного відрізку.

Ці дві властивості множин дійсних чисел (властивість безперервності і властивість континуальності) дозволяють надалі проводити математичний аналіз безперервних змінних величин на будь-якому проміжку.

Помітимо, що кінцевий числовий відрізок еквівалентний по потужності одиничному відрізку, якщо зробити заміну змінною , .

Розглянемо далі деякі, числові множини, які часто використовуються.