28

2. Основи лінійної алгебри

Однієї з основних задач лінійної алгебри є розв‘язання систем лінійних алгебраїчних рівнянь. До таких систем зводяться багато задач математичного моделювання фізичних і технологічних процесів при їх дискретизації, тобто представлення відповідних диференціальних рівнянь через кінцеві різниці або кінцеві елементи. Використовуючи алгебру матриць, система лінійних рівнянь алгебри представляється в найбільш простий і компактній формі

А X = B, (2.1)

де А – матриця коефіцієнтів системи рівнянь (основна матриця), X – матриця-стовпець невідомих, В – матриця-стовпець вільних членів. Тому зручно проводити дослідження вирішень системи (2.1), використовуючи мову матриць.

2.1. Поняття матриці

Визначення 2.1. Матрицею називається прямокутна таблиця з n × m чисел, яка містить m рядків і n стовпців.

Позначення: або . (2.2)

Або коротко [а _ij ] ( i = 1,2,…, n ; j = 1,2,..,m ) . В цьому випадку мається на увазі, що матриця має розмірність n × m. Матриці позначають заголовними латинськими буквами А, В, С, D ... Числа a_ij називаються елементами матриці, де перший індекс i означає номер рядка, а другий _j - номер стовпця.

Якщо в квадратній матриці всі елементи головної діагоналі дорівнюють одиниці, а всі інші дорівнюють нулю, то її називають одиничною матрицею. Вона позначається буквою Е і має вигляд

. (2.3)

Визначення 2.2. Дві матриці А і В називаються рівними, якщо вони мають однакову кількість рядків і стовпців і відповідні елементи яких збігаються.

Матриця, в якій всі елементи дорівнюють нулю, називається нуль-матрицею або нульовою. Її позначають буквою О.

Якщо матриця складається лише з одного рядка, то вона називається матрицею-рядком. Матриця, що складається з одного стовпця називається матрицею-стовпцем.

Якщо в матриці А поміняти рядки на стовпці, а стовпці – на відповідні рядки, то отриману матрицю називають транспонованою і позначають А^T .

2.2. Дії над матрицями

Додавання.

Операція додавання матриць вводиться лише для матриць однакових розмірів.

Визначення 2.3. Сумою двох матриць і називаєть-ся матриця така, що

Приклад

+ = .

Аналогічно визначається різниця матриць.

Множення на число

Визначення 2.4. Добутком матриці на число k називається матриця така, що

Приклад

А = , k = 2, A∙k = .

Різницю матриць А – В можна визначити так: А – В = А +(–1)∙В.

Операції додавання і множення матриці на число мають наступні властивості:;

1. А + (В + С) = (А + В) + С; 6. α ∙(А + В)= α ∙А + α ∙В;

2. А + О = А ; 7. (α + β)∙А = α ∙А + β ∙А;

3. А – А = О; 8. α ∙ ( β ∙ А) = (α ∙ β) ∙ А ,

де А, В, С – матриці, α, β – числа.

Добуток матриць.

Операція множення двох матриць уводиться тільки для випадку, коли число стовпців першої матриці дорівнює числу рядків другої матриці.

Визначення 2.5. Добутком матриці на матрицю називається матриця така, що

,

тобто елемент i-ої рядка й k-го стовпця матриці добутку С дорівнює сумі добутків елементів i-ого рядка матриці А на відповідні елементи k-го стовпця матриці В.

Одержання елемента схематично зображується так:

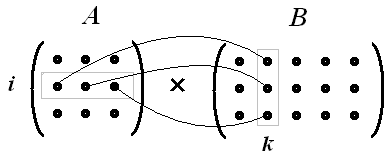
Якщо матриці А і В квадратні одного розміру, то добуток А В і В А завжди існують. Легко показати, що А Е = Е А = А , де А - квадратна матриця, Е - одинична матриця того ж розміру.

Приклад

, . Тоді добуток матриць А В визначається в таким чином:

А В = ∙ = = .

При цьому добуток В А не визначено, тому що число стовпців матриці В(3) не збіжиться із числом рядків матриці А(2).

Матриці А і В називаються переставними, якщо АВ = ВА.

Множення матриць має наступні властивості:

1. А ∙ (В ∙ С) = (А ∙ В) ∙ С; 3. (А + В) ∙ С = А∙С + В∙С ;

2. А ∙ (В + С) = А∙В + А∙С ; 4. α ∙ (А ∙ В) = (α∙А) ∙ В ,

якщо, звичайно, написані суми й добутки матриць мають сенс.

Для операції транспонування вірні властивості:

1. (А+В)^Т = А^Т + В^Т; 2. (А∙В)^Т = А^Т ∙ В^Т.