3.3.2. Аналітична геометрія на площині

Загальне рівняння прямої А х + В у + С = 0. (3.35)

Рівняння прямої з кутовим коефіцієнтом y = k ∙x + b . (3.36)

Рівняння прямої, що проходить через дві точки М₁(х₁,у₁) і М₂(х₂,у₂)

. (3.37)

Рівняння прямої у відрізках . (3.38)

Кут між двома прямими 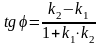. (3.39)

Умова паралельності двох прямих k₂ = k₁ . (3.40)

Умова перпендикулярності двох прямих k₁ ∙ k₂ = - 1. (3.41)

Відстань від точки М₀(х₀,у₀) до прямої d = . (3.42)

Приклади

1). Знайти кут між площиною 3x − 2 y + z + 4 = 0 і прямою .

Розв’язування. Рівняння прямої приведено до канонічного вигляду. Із першого рівняння знаходимо 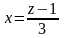, а з другого рівняння , значить канонічний вид рівняння прямої буде . Таким чином, направляючий вектор прямої = (1; 2; 3) , а нормальний вектор площини = (A,B,C) = (3, -2, 1).

Тепер за формулою (3.32) знаходимо синус кута між прямою і площиною

.

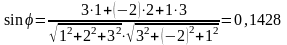2). Записати рівняння площини, що проходить через точки M₁ ( 8; 3;1 ) і

M₂ ( 4;7 ;2 ) і перпендикулярна до площини 3x + 5 y −7z + 21 = 0 .

Розв’язування. Тому що площина проходить через точку М₁ ( 8; 3;1 ) , то її

rоординати задовольняють рівняння (3.20), тобто

A( x − 8 ) + B( y + 3 ) + C( z − 1 ) = 0 . (*)

Аналогічно, площина проходить і через точку M₂ ( 4;7 ;2 ) , то

її координати задовольняють рівнянню (2.79), тобто

A( 4 − 8 ) + B( 7 + 3 ) + C( 2 − 1 ) = 0 .

Використаємо умову перпендикулярності (3.25) для площини

(*) і заданої площини 3x + 5y -7z + 21= 0, тобто 3A + 5B - 7C = 0. Для

Знаходження А, В, С маємо систему двох рівнянь з трьома невідомими, а

саме . З даної системи знаходимо A і B через C , тобто

, і підставляємо одержані значення в рівняння (*):

. Зробивши спрощення в останньому рівнянні , одержуємо шукане рівняння площини 3x + y + 2z – 23 = 0.

3). Знайти довжину бісектриси АЕ і площу трикутника АВС, якщо

і .

Знайдемо площу трикутника. S = кв. од. Використовуючи властивість бісектриси , знайдемо відношення , у якому точ­ка Е поділяє відрізок СВ; . Знайдемо координати точки : .

Отже, .

4). Скласти рівняння бісектрис кутів, утворених двома прямими

і .

Бісектриса є множиною точок, рівновіддалених від сторін кута. Нехай

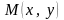— одна з точок цієї множини. Тоді, прирівнюючи відстані від цієї

точки до прямих, маємо:

.

З останнього рівняння маємо рівняння двох бісектрис у вигляді:

і . Слід зазначити, що бісектриси взаємно перпендикулярні: .

5). Дано трикутник 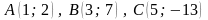. Знайти відстань від вершини В

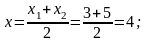
до медіани, що проходить через точку А. Знайдемо координати основи медіани: . Запишемо рівняння медіани як прямої, що проходить через дві задані точки: , або .

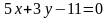Відстань від точки до медіани знайдемо за формулою:

.