77

3. Векторна алгебра і аналітична геометрія

3.1. Основні поняття і формули векторної алгебри

Вектор AB є спрямований відрізок прямої, у якого один кінець (точка А) називається початком вектору, а інший кінець (точка В) - кінцем вектора.

Використовуючи координатний метод всякий вектор в заданій просторовій декартовій системі координат представляється алгебраїчним об'єктом у вигляді впорядкованої трійки чисел (x, y, z), де x, y, z - координати радіус-вектора AB (точка А - початок координат), або координати кінця В вектора AB.

Довжиною (модулем) вектора називається відстань між початком і кінцем вектора.

, (3.1)

де координати точок А(0,0,0) - початок координат (початок вектора), а точка В (кінець вектора) має координати x, y, z , отже В(x, y, z).

Напрям вектора визначається так званими направляючими косинусами

де , , відповідно кути між осями координат x, y, z і вектором .

Якщо відомі координати початку А(х₁,у₁,z₁) і кінця В(х₂,у₂,z₂) в ектора AB,

те довжина цього вектора дорівнює

d = | AB | = . (3.3)

Орт вектора AB, якій має одиничну довжину і напрям якого співпадає з вектором AB, визначається відношенням

Дії над векторами

Сума векторів. Хай 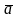і два довільні вектори. Візьмемо довільну точку О і побудуємо вектор . Від точки А (кінець вектора ) відкладемо вектор . Вектор, який сполучає початок першого вектору з кінцем другого, називається сумою векторів і : (див. рис. 3.1 і рис 32).

Це правило складання векторів називають правилом трикутника.

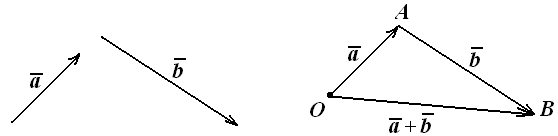
Рис. 3.1. Складання векторів за правилом трикутників

Суму двох векторів можна побудувати також за правилом паралелограма

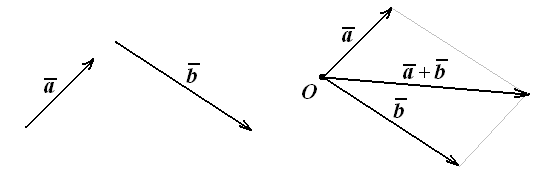
Рис. 3.2. Складання векторів за правилом паралелограма.

Різниця векторів. Під різницею векторів і розуміється вектор такий, що 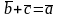(рис. 3.3)

Рис. 3.3. Різниця векторів.

Якщо вектори і задані своїми координатами (a_x, a_y, a_z), (b_x, b_y, b_z), то координати суми (різниці) векторів визначаються по формулах

с_x = a_x ± b_x , с_y = a_y ± b_y, с_z= a_z ± b_z . (3.5)

Добутком k вектору на число k називається вектор, колінеарний вектору , модуль його рівний |k||a|, а напрям, співпадає з напрямом при k > 0 і протилежний при k < 0.

В координатній формі, якщо (a_x, a_y, a_z), тоді вектор k -

k =(ka_x,k a_y,k a_z). (3.6)

Проекція вектора на вісь. Проекцією вектора АВ на вісь х називається довжина вектора А₁В₁, узята зі знаком "+", якщо напрям А₁В₁ співпадає з напрямом осі х, зі знаком "-", якщо напрям А₁В₁ протилежний напряму осі х (рис.3.4).

Пр_х АВ = ± | А₁В₁ |. (3.7)

Рис. 3.4. Проекція вектора АВ на вісь х

Скалярний добуток. Скалярним добутком, двох векторів називається добуток їх довжин і косинуса кута між ними.

Скалярний добуток двох векторів а і b позначаємо символом a∙b. Відповідно до визначення

a ∙ b = | a | | b | cos(a ^ b). (3.8)

Кут між векторами визначається як

cos(a ^ b) = . (3.9)

Звідки витікає, що умова ортогональності двох векторів(а _┴ b)

a ∙ b = 0. (3.10)

Скалярний добуток через координати векторів визначається за формулою

∙ = a_x b_x + a_y b_y + a_z b_z . (3.11)

Проекція вектора (a_x, a_y, a_z) на вектор (b_x, b_y, b_z)

. (3.12)

Векторний добуток. Векторний добуток двох векторів і є вектор , модуль якого дорівнює добутку модулів векторів - співмножників, перпенди-кулярний площині цих векторів і спрямований так, що з його кінця видно поворот від до по найкоротшому шляху, проти ходу годинникової стрілки.

= , (3.13)

Тобто вектор задовольняє наступним умовам

1. | | = | | = | | | | sin( ^ ) ;

2. _┴ , _┴ ;

3.

Рис. 3.5. Векторний добуток [ ].

Умова паралельності. Якщо вектори і колінеарні ( || ), то їх векторний добуток дорівнює нулю

[ ] = 0. (3.14)

Векторний добуток через координати векторів визначається за формулою

= . (3.15)

Мішаний добуток. Скалярний добуток вектора на векторний добуток векторів і називається мішаним добутком векторів , і . Таким чином, мішаний добуток векторів є вираз

∙ ( ) (3.16)

і є скаляр (число).

Якщо вектори задані своїми координатами в деякій декартовій прямокутній системі координат (a_x , a_y , a_z) , (b_x , b_y , b_z), (c_x , c_y , c_z) , тому

вектор

∙ ( ) = . (3.17)

Якщо три вектори , і компланарні (знаходяться в однієї площині), то їх мішаний добуток дорівнює нулю

∙ ( ) = 0 (3.18)

Приклади

1). Дано три послідовні вершини паралелограма:

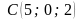. Знайти його четверту вершину.

Нехай шукана вершина має координати . З умови колінеарності векторів і маємо: , або 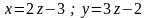. Згідно з властивостями паралелограма 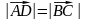або . Отже

.

2). Знайти площу паралелограма, діагоналями якого є вектори і

, де і — одиничні вектори, а кут між ними дорівнює 45.

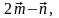
Позначимо через сторони паралелограма, тоді 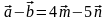, звідки . Площу паралелограма знайдемо як модуль векторного добутку . Отже, .

3). Знайти площу і висоту трикутника, вершинами якого є:

.

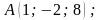
Знайдемо вектори і . Модуль їх векторного

добутку буде дорівнювати подвоєній площі трикутника: звідки .

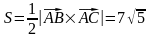Знайдемо висоту трикутника: .

4). Дано вершини трикутника А(−1, −2, 4); В(−4, −2, 0); С(3, −2, 1).

Визначити його внутрішній кут φ при вершині B.

Знайдемо вектори BA= (3, 0, 4), BC = (7, 0, 1) та їх довжини:

BA = = 5, BC = = .

За формулою (3.9) обчислимо косинус кута φ між векторами

cos(a ^ b) = = ,

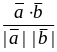отже φ = 45⁰ .

5). Дано три вектори =(1, −3, 4), =(3, −4, 2), = (−1,1, 4).

Знайти

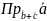
Введемо вектор = = (2, − 3, 6) , та обчислимо його довжину

| d |= = 7

За формулою (3.12) знайдемо проекцію вектора на вектор

.
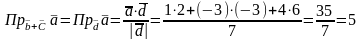