29

2. Основы линейной алгебры

Одной из основных задач линейной алгебры является решение систем линейных алгебраических уравнений. К таким системам сводятся многие задачи математического моделирования физических и технологических процессов при их дискретизации, т.е. представления соответствующих дифференциальных уравнений через конечные разности или конечные элементы. Используя алгебру матриц, система линейных алгебраических уравнений представляется в наиболее простой и компактной форме

А X = B, (2.1)

где А – матрица коэффициентов системы уравнений (основная матрица), X – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Поэтому удобно проводить исследование решений системы (2.1), используя язык матриц. Рассмотрим элементы алгебры матриц.

2.1. Понятие матрицы

Определение 2.1. Матрицей называется прямоугольная таблица из n × m чисел, которая содержит m строк и n столбцов.

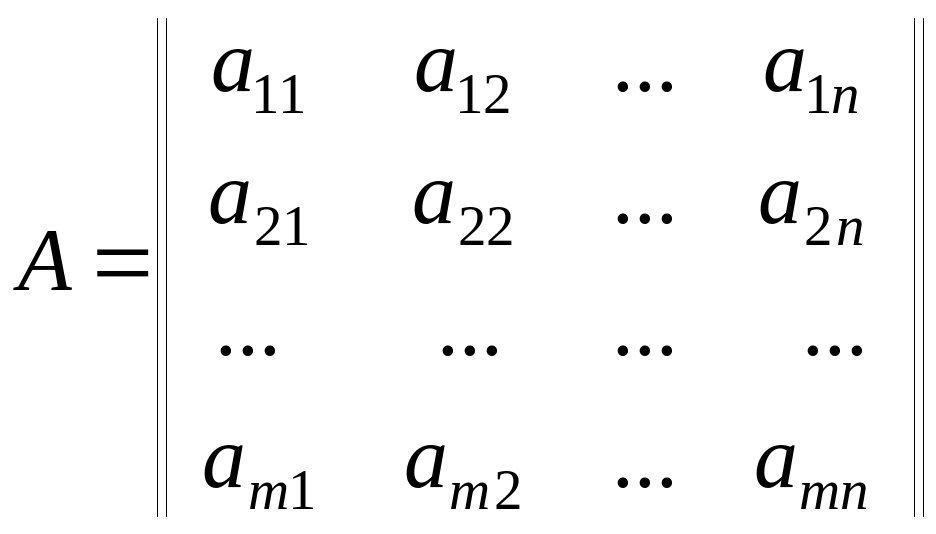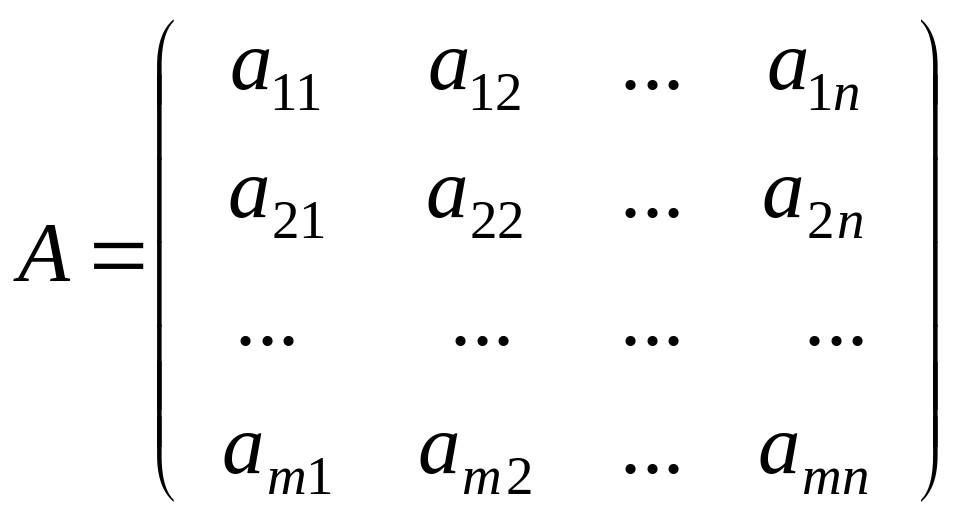Обозначения: или . (2.2)

Либо кратко [а _ij ] ( i = 1,2,…, n ; j = 1,2,..,m ). В этом случае имеется в виду, что матрица имеет размерность n × m . Матрицы обозначают заглавными латинскими буквами А, В, С, Е, ... Числа a_ij называются элементами матрицы, где первый индекс i означает номер строки, а второй j - номер столбца.

Если в квадратной матрице все элементы главной диагонали равны единице, а все остальные равны нулю, то её называют единичной матрицей. Она обозначается буквой Е и имеет вид

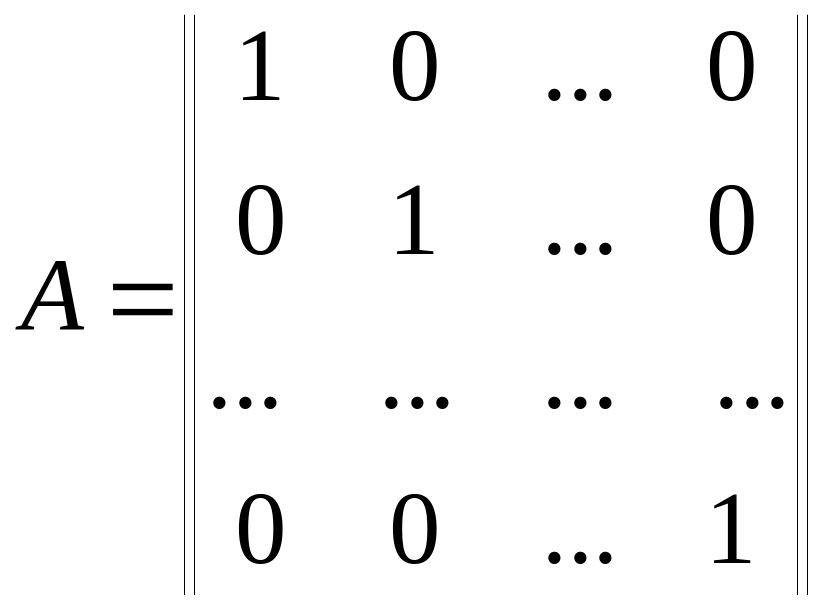. (2.3)

Определение 2.2. Две матрицы А и В называются равными, если они имеют одинаковое количество строк и столбцов и соответствующие элементы которых совпадают.

Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Её обозначают буквой О.

Если матрица состоит только из одной строки, то она называется матрицей-строкой. Матрица, состоящая из одного столбца называется матрицей-столбцом.

Если в матрице А поменять строки на столбцы, а столбцы – на соот-ветствующие строки, то полученную матрицу называют транспонированной и обозначают А^T.

2.2. Действия над матрицами

Сложение.

Операция сложения матриц вводится только для матриц одинаковых размеров.

Определение 2.3. Суммой двух матриц и называется матрица такая, что .

Пример

+ = .

Аналогично определяется разность матриц.

Умножение на число

Определение 2.4. Произведеним матрицы на число k называется матрица такая, что

Пример

А = , k = 2, A∙k = .

Разность матриц А – В можно определить так: А – В = А +(– В).

Операции сложения и умножения матрицы на число обладают следующими свойствами:

1. А + В = В + А; 5. 1 ∙ А =А;

2. А + (В + С) = (А + В) + С; 6. α ∙(А + В)= α ∙А + α ∙В;

3. А + О = А ; 7. (α + β)∙А = α ∙А + β ∙А;

4. А – А = О; 8. α ∙ ( β ∙ А) = (α ∙ β) ∙ А ,

где А, В, С – матрицы, α, β – числа.

Произведение матриц.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Определение 2.5. Произведением матрицы на матрицу называется матрица такая, что

,

т.е. элемент i-ой строки и k го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Получение элемента схематично изображается так:

Если матрицы А и В квадратные одного размера, то произведение А∙В и В∙А всегда существуют. Легко показать, что А∙Е = Е∙А=А , где А – квадратная матрица, Е – единичная матрица того же размера.

Пример

, . Тогда произведение матриц А В определяется следующим образом:

А В = ∙ = = .

При этом произведение В А не определено, так как число столбцов матрицы В(3) не совпадет с числом строк матрицы А(2).

Матрицы А и В называются перестановочными, если АВ = ВА.

Умножение матриц обладает следующими свойствами

1. А ∙ (В ∙ С) = (А ∙ В) ∙ С; 3. (А + В) ∙ С = А∙С + В∙С ;

2. А ∙ (В + С) = А∙В + А∙С ; 4. α ∙ (А ∙ В) = (α∙А) ∙ В ,

если, конечно, написанные суммы и произведения матриц имеют смысл.

Для операции транспонирования верны свойства:

1. (А+В)^Т = А^Т + В^Т; 2. (А∙В)^Т = А^Т ∙ В^Т.