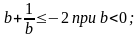Неравенства

1. Свойства неравенств:

а) при умножении или делении неравенства на положительное число

смысл неравенства не меняется;

б) при умножении или делении неравенства на отрицательное число

смысл неравенства меняется на противоположный;

в) прибавление или вычитание одного и того же числа к каждой части

неравенства не меняет смысла неравенства;

г) замена деления умножением при нулевой правой части:

если , то A∙B < 0;

если , то A∙B > 0;

2. Квадратные неравенства a∙x² + b∙x + c < 0 или > 0 при a > 0.

а) D = b² − 4∙a∙c > 0;

x_м , x_б – корни квадратного трехчлена a∙x² + b∙x + c = 0;

если a∙x² + b∙x + c < 0, то одно решение: x_м < x < x_б;

если a∙x² + b∙x + c > 0, то два решения: x < x_м и x > x_б;

б) D = b² − 4∙a∙c < 0;

нет корней;

если a∙x² + b∙x + c < 0, то нет решения, т.е. x Ø;

если a∙x² + b∙x + c > 0, то решение: −∞ < x < +∞;

3. Логарифмирование неравенств

если M < N, то

при a > 1 log_aM < log_aN; (смысл неравенства не меняется)

при 0 < a < 1 log_aM > log_aN; (смысл неравенства меняется

на противоположный)

4. Потенцирование неравенств (избавление от логарифмов)

если log_aM < log_aN, то

при a > 1 0 < M < N; (смысл неравенства не меняется)

при 0 < a < 1 M > N > 0; (смысл неравенства меняется

на противоположный)

5. Показательные неравенства

если a^M < a^N, то (обязательно a = const;)

при a > 1 M < N (смысл неравенства не меняется)

при 0 < a < 1 M > N (смысл неравенства меняется

на противоположный)

6. Модули

если │A│ < 5, то −5 < A < 5;

если │A│ > 7, то A > 7 или A < −7;

если │A│ > −3, то −∞ < A < +∞;

если │A│ < −2, то неравенство не имеет смысла, т.е. A Ø;

= ;

= ;

7. Возведение в квадрат возможно только тогда, когда обе части

неравенства положительны.

8. Возведение в куб возможно всегда.

9. График квадратного трёхчлена:

парабола y = a∙x² + b∙x + c;

вершина параболы: точка A(x₀ , y₀)

x₀ = −

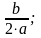
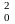y₀ = a∙x + b∙x + c; (подставляем x₀ в уравнение параболы)

направление ветвей параболы:

при a > 0 вверх;

при a < 0 вниз;

точка пересечения с осью oy: при x = 0 y = c;

точки пересечения с осью ox: корни x₁ и x₂;

10. График гиперболы (обязательно должно быть m ≠ 0) :

вертикальная асимптота: m∙x + n = 0; x = −

горизонтальная асимптота: y =

точка пересечения с осью oy: при x = 0 y = 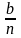; (при n ≠ 0)

если встречается случай n = 0, то гипербола не пересекает ось oy;

точка пересечения с осью ox: a∙x + b = 0; x = − (при a ≠ 0)

если a = 0, то гипербола не пересекает ось ox.

11. Разложение квадратного трёхчлена на множители

a∙x² + b∙x + c = a∙(x – x₁)∙(x – x₂),

где x₁ и x₂ – корни трёхчлена;

12. Некоторые классические неравенства: