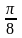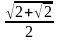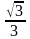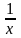Математика
Конспект
для абитуриентов
Киев - 1981 Оглавление
Логарифмы……………………….3
Степени…………………………...4
Квадратные уравнения…………..5
Модули………………………..….6
Тригонометрия…………………...7
Неравенства…………… ……….17
Планиметрия…………………….21
Стереометрия…………………....26
Графики………………………….30
10. Производная……………………..41
11. Интеграл………………………….46
12. Векторы и координаты……….....51
13. Разное…………………………….56
14. Теория вероятностей и
математической статистики…….62
Логарифмы
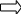
Определение: log a N = k ak = N ; N > 0 , a > 0 , a ≠ 1;
log c (a∙b) = log c a + log c b ;
log c
 =
log c
a
− log c
b
;
=
log c
a
− log c
b
;
log c an = n∙log c a ;

 − основное
логарифмическое тождество
− основное
логарифмическое тождествоlog c a =
 ;
− формула перехода
;
− формула переходаl og b a∙log a b = 1 ; log b a =
 ;
;

9. log a a = 1 ;
10. log a 1 = 0 ;
11.


Логарифмы бывают трёх видов:
1) общего вида log a b ;
2) десятичные логарифмы lg x = log 10 x ;
3) натуральные логарифмы ln x = log e x ,
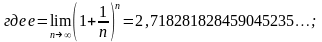
Степени
am ∙ an = am+n;
 = am
− n;
= am
− n; = am∙n;
= am∙n;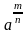 =
=
 ;
;a–n =
 ;
;a0 = 1 при a ≠ 0; (00 – смысла не имеет)
 =
=
 ;
;an ∙ bn = (a ∙ b)n;
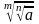 =
=
 ;
; =
;
=
;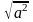 =
=
 ;
; =
=
 ;
;
Квадратные уравнения
a∙x2 + b∙x + c = 0; b − нечетное;
D = b2
− 4∙a∙c; x1,2
=
 ;
;
a∙x2 + b∙x + c = 0; b − чётное;
D =
 − a∙c; x1,2
=
− a∙c; x1,2
=
 ;
;
x2 + p∙x + q = 0; p − чётное;
D =
 − q; x1,2
= −
− q; x1,2
= − ;
;
Теорема Виета для квадратного уравнения:
x2 + p∙x + q = 0;
x1 + x2 = −p;
x1 ∙ x2 = q;
Модули
Определение модуля:
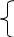 a
при a
≥ 0;
a
при a
≥ 0;
│a│ =
–a при a < 0;
Если │A│ = 5, то A = 5 или A = −5;
Если │A│ = −2, то равенство не имеет смысла, т.е. A
 Ø;
Ø;Если │A│ = 0, то A = 0;
= ;

Если │A│ < 5, то −5 < A < 5;
Если │A│ > 7, то A > 7 или A < −7;
Если │A│ > −3, то −∞ < A < +∞;
Если │A│ < −2, то неравенство не имеет смысла, т.е. A Ø;
Тригонометрия
Единицы измерения углов:
градус −
 часть окружности;
часть окружности;
минута −
 часть градуса;
часть градуса;
секунда − часть минуты;
радиан − центральный угол, длина дуги которого равна его радиусу;
1 радиан =
 57°17´44,806˝;
57°17´44,806˝;
π радиан = 180°;
1° =
 0,017 453 292 519 943 радиана;
0,017 453 292 519 943 радиана;
π =
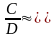 3,14 159 265 358 979 323 846 264…
3,14 159 265 358 979 323 846 264…
Знаки по четвертям
sinα ; cosecα cosα ; secα tgα ; ctgα
+ + − + − +
− − − + + −
Периоды тригонометрических функций
sin(x + 2∙k∙π) = sin x; T = 2∙π;
cos(x + 2∙k∙π) = cos x; T = 2∙π;
tg(x + k∙π) = tg x; T = π;
ctg(x + k∙π) = ctg x; T = π;
Основные соотношения между функциями одного и того же аргумента
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
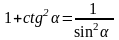 ;
;
Изменение знака аргумента
(чётность и нечётность функций)
sin(−x) = −sin x; нечётная
cos(−x) = cos x; чётная
tg(−x) = −tg x; нечётная
ctg(−x) = −ctg x; нечётная
sec(−x) = sec x; чётная
cosec(−x) = −cosec x; нечётная
6. Формулы приведения
1) номер четверти;
2) знак функции в этой четверти;
3) “негритянское” правило:
π или 2∙π (горизонтальная ось−нет) − не менять на кофункцию;
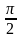 или
или
 (вертикальная ось−да) − менять на
кофункцию;
(вертикальная ось−да) − менять на
кофункцию;
7. Обратные тригонометрические функции
y = arcsin x y = arccos x


−1
≤ x ≤ 1
 ≤ arcsin x ≤
0 ≤ arcos x ≤ π
≤ arcsin x ≤
0 ≤ arcos x ≤ π
y = arctg x

y = arcctg x

−∞ < x < +∞ < arctg x < 0 < arcctg x < π
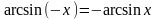 ;
;
 ;
;
 ;
;
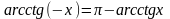 ;
;
 при −1 ≤ x
≤ 1;
при −1 ≤ x
≤ 1;
 при −1 ≤ x
≤ 1;
при −1 ≤ x
≤ 1;
 при
−∞ < x
< +∞;
при
−∞ < x
< +∞;
 при
−∞ < x
< +∞;
при
−∞ < x
< +∞;
 при
при
 ;
;
 при
при
 ;
;
 при
при
 ;
;
 при
при
 ;
;
 при −1 ≤ x
≤ 1;
при −1 ≤ x
≤ 1;
 при
−∞ < x
< +∞;
при
−∞ < x
< +∞;
8. Таблица значений тригонометрических функций для некоторых
значений аргумента
α градусы |
0° |
15° |
22°30´ |
30° |
45° |
60° |
67°30´ |
75° |
90° |
α радианы |
0 |
|
|
|
|
|
|
|
|
sinα |
0 |
|
|
|
|
|
|
|
1 |
cosα |
1 |
|
|
|
|
|
|
|
0 |
tgα |
0 |
|
|
|
1 |
|
|
|
не сущ. |
ctgα |
не сущ. |
|
|
|
1 |
|
|
|
0 |
9. Решение простейших тригонометрических уравнений
Общие формулы:
1)

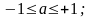
 k
Z
;
k
Z
;
2)

 k
Z
;
k
Z
;
3)


 k
Z
;
k
Z
;
4)
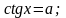
 k
Z
;
k
Z
;
Частные случаи:

 k
Z
;
k
Z
;

 k
Z
;
k
Z
;
 k
Z
;
k
Z
;

 k
Z
;
k
Z
;

 k
Z
;
k
Z
;

 k
Z
;
k
Z
;

 k
Z
;
k
Z
;

 k
Z
;
k
Z
;

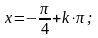 k
Z
;
k
Z
;
10. Формулы суммы и разности двух аргументов








11. Формулы двойного аргумента




12. Формулы тройного аргумента
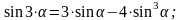



13. Формулы половинного аргумента




14. Выражение через тангенс половинного аргумента
Если
 , то
, то




15. Преобразование суммы в произведение


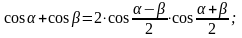






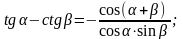








16. Преобразование произведения в сумму




 формулы
формулы
 понижения
степени
понижения
степени
17. Выражение произведения через сумму
1)
если
 , то
, то

2)
если
 , то
, то

18. Формулы тройного аргумента




19. Некоторые числовые значения

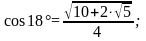






Вывод
этих формул:
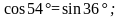


сокращаем далее на cos18° и т.д.
20. Вычисление прямых функций от обратных
обратные прямые |
arcsin x |
arccos x |
arctg x |
arcctg x |
sin |
x |
|
|
|
cos |
|
x |
|
|
tg |
|
|
x |
|
ctg |
|
|
|
x |
21. Геометрическая интерпретация тригонометрических функций