РГР№1. Чечулина

Министерство образования и науки РФ

Уфимский Государственный Авиационный Технический Университет

Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1

«РАСЧЕТ ЛИНЕЙНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА»

Выполнил:

Студент группы

Приняла:

Уфа 2005.

Вариант 128307 - 2

R1=30	R2=30	R3=90
R4=40	R5=50	R6=20
Е1=-250	Е2=0
Е3=0	Е4=0
Е5=0	Е6=200
IК1=0	IК2= - 8
IК3= 0

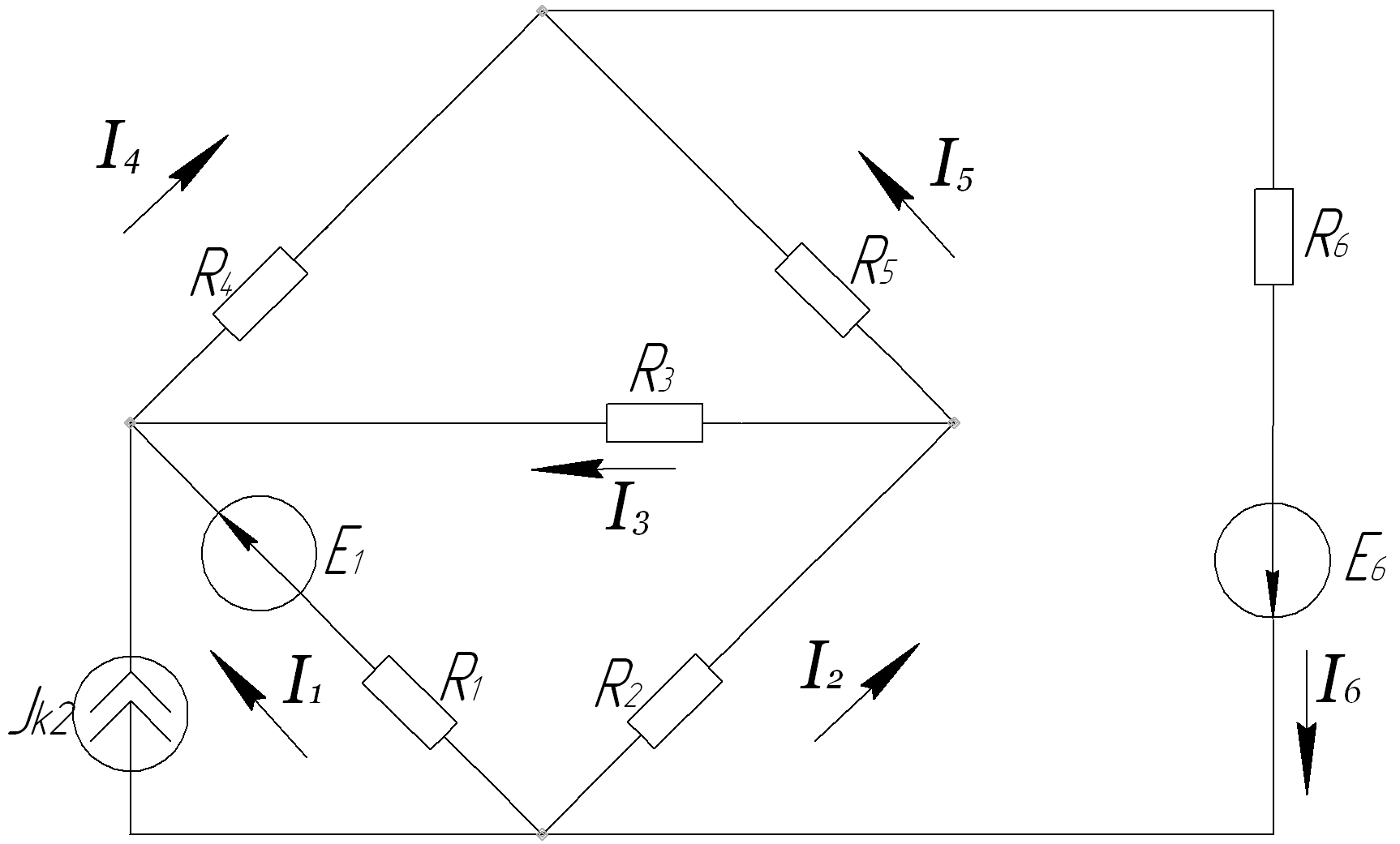
1. Расчёт цепи методом контурных токов

Введём контурные токи I₁₁,I₂₂,I₃₃, I₄₄, причём контурный ток I₁₁ является известным и равным току источника тока IК₂:

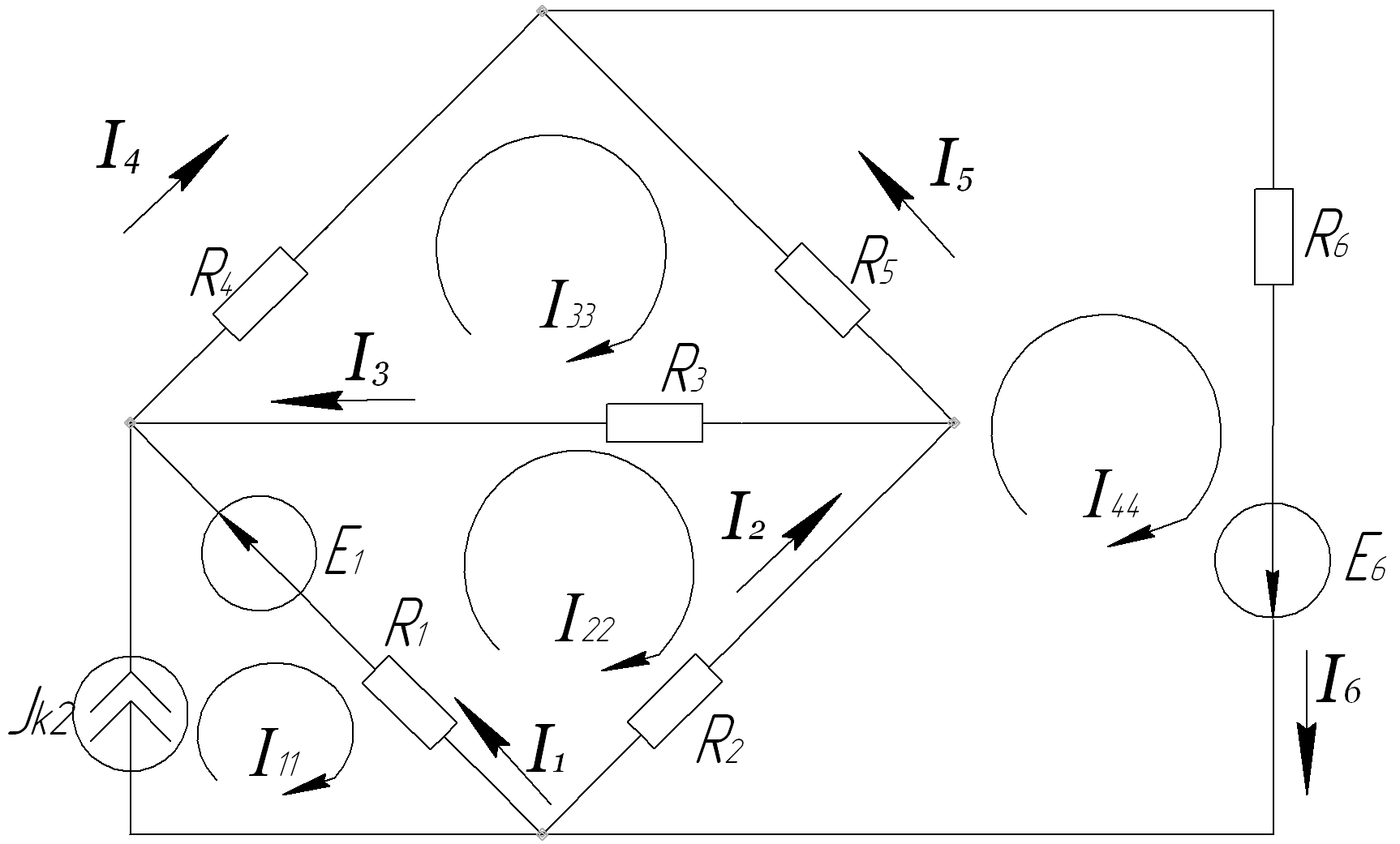I₁= I₂₂ – I₁₁

I₂= I₄₄ – I₂₂

I₃= I₃₃ – I₂₂

I₄= I₃₃

I₅= I₄₄ – I₃₃

I₆= I₄₄

Запишем уравнения по методу контурных токов:

I₁₁ = IК₂

R₂₁ I₁₁ + R₂₂ I₂₂ + R₂₃ I₃₃ + R₂₄ I₄₄ = E₂₂

R₃₁ I₁₁ + R₃₂ I₂₂ + R₃₃ I₃₃ + R₃₄ I₄₄ = E₃₃

R₄₁ I₁₁ + R₄₂ I₂₂ + R₄₃ I₃₃ + R₄₄ I₄₄ = E₄₄

I₁₁ = IК₂

–R₁ I₁₁ + (R₂+R₃+R₁)I₂₂ – R₃ I₃₃ – R₂I₄₄ = E₁

0 I₁₁ – R₃ I₂₂ + (R₄+R₅+R₃)I₃₃ – R₅I₄₄ = 0

0 I₁₁ – R₂ I₂₂ – R₅ I₃₃ + (R₂+R₅+R₆)I₄₄= E₆

(R₂+R₃+R₁)I₂₂ – R₃ I₃₃ – R₂I₄₄ = E₁ + R₁IК₂

R₃I₂₂ + (R₄+R₅+R₃)I₃₃ – R₅I₄₄ = 0

R₂I₂₂ – R₅ I₃₃ + (R₂+R₅+R₆)I₄₄= E₆

150I₂₂ – 90 I₃₃ – 30 I₄₄ = –250 + 30(–8)

–90I₂₂ + 180I₃₃ – 50 I₄₄ = 0

–30I₂₂ – 50 I₃₃ + 100I₄₄ = 200

Составим матрицу и найдём контурные токи:

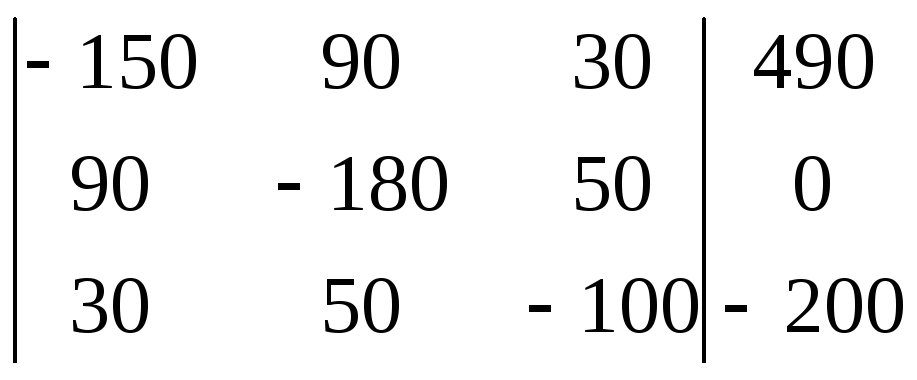
I₁₁ = –8А, I₂₂ = -5,185A, I₃₃ = -2,867A, I₄₄ = -0,9889A

Находим реальные токи

2. Расчёт цепи методом узловых потенциалов

Определяем количество необходимых уравнений n = У – 1 = 4 – 1 = 3.

Приняв потенциал точки 4 равным нулю, запишем систему уравнений

φ₁ G₁₁ + φ₂ G₁₂ + φ₃ G₁₃ = I₁₁

φ₁ G₂₁ + φ₂ G₂₂ + φ₃ G₂₃ = I₂₂

φ₁ G₃₁ + φ₂ G₃₂ + φ₃ G₃₃ = I₃₃

Определяем взаимную и собственную проводимости

Составим матрицу и найдём потенциалы точек

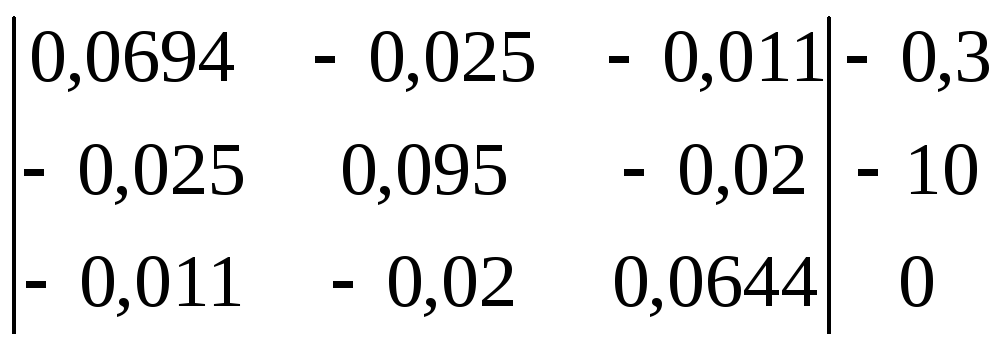
φ₁ = – 334,45 В φ₂ = – 248,44 В φ₃ = – 125,883 В φ₄ = 0 В

Пользуясь законом Ома, определяем токи во всех ветвях

Таблица токов

Токи	I1,А	I2,А	I3,А	I4,А	I5,А	I6,А
МКТ	2,815	4,1961	2,318	- 2,867	1,8781	- 0,9889
МУП	2,815	4,196	2,318	- 2,8674	1,878	- 0,9889

3. Проверка по законам Кирхгофа:

В схеме 4 узла, проверим первый закон Кирхгофа:

1: I₄ – I₃ – I₁ – Iк₂= –2,867–2,318 – 2,815 – (–8) = 0

2: – I₄ – I₅ + I₆ = 2,867 – 1,8781 – 0,9889 = 0

3: I₅ + I₃ – I₂ = 1,8781 +2,318 – 4,1961 = 0

4: I₁ + I₂ – I₆ + Iк₂= 2,815 + 4,1961 + 0,9889 – 8 = 0

Проверим второй закон Кирхгофа, в схеме 3 независимых контура, не содержащих источников тока:

1: I₃ R₃ + I₄ R₄ – I₅ R₅ = 0

208,62 – 114,68 – 93,905 = 0,00035 В≈ 0 В (выполняется)

2: I₁ R₁ – I₃ R₃ – I₂ R₂ = E₁

84,45 – 208,62 – 125,883 = – 250,053 В≈ –250 В (выполняется)

3: I₅ R₅ + I₆ R₆ + I₂ R₂ = E₆

93,905 – 19,778 + 125,883 = 200,01 В ≈ 200 В (выполняется)

Законы Кирхгофа выполняются, значит, токи найдены правильно.

4. Баланс мощностей

ΣP_ист = ΣP_пр.

ΣP_ист = ΣP_E + ΣP_J

ΣP_E = E₁ I₁ + E₆ I₆ = –250∙2,815 + 200∙(–0,9889) = –901,53 Вт

ΣP_J = U_Jk2 J_k2

Из второго закона Кирхгофа найдём U_Jk2

U_Jk2 +I₂R₂ + I₃R₃ = 0

U_Jk2 = –(I₂R₂ + I₃R₃) = –334,503 В

ΣP_J = U_Jk2 J_k2 = –334,503∙(–8) = 2676,024 Вт

ΣP_ист = ΣP_E + ΣP_J = 1774,494 Вт

ΣP_пр = R₁ I₁² + R₂ I₂² + R₃ I₃² + R₄ I₄² + R₅ I₅² + R₆ I₆² = 237,72675 + 528,2176563 + 483,58116 + +328,78756 + 93,905 + 19,5584642 = 1774,234571 Вт

ΣPист = 1774,494 ≈ 1774,234571 = ΣPпр

ΣPист ΣPпр

Баланс соблюдается.

5. Определение тока I₁ методом эквивалентного генератора

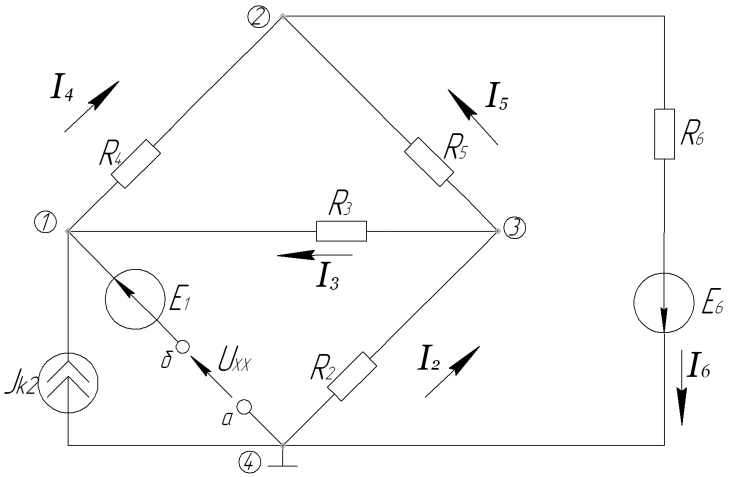
Сначала определим потенциалы 1-го узла в отсутствии сопротивлением R₁, приняв потенциал 4-го узла за ноль.

φ₁ G₁₁ + φ₂ G₁₂ + φ₃ G₁₃ = I₁₁

φ₁ G₂₁ + φ₂ G₂₂ + φ₃ G₂₃ = I₂₂

φ₁ G₃₁ + φ₂ G₃₂ + φ₃ G₃₃ = I₃₃

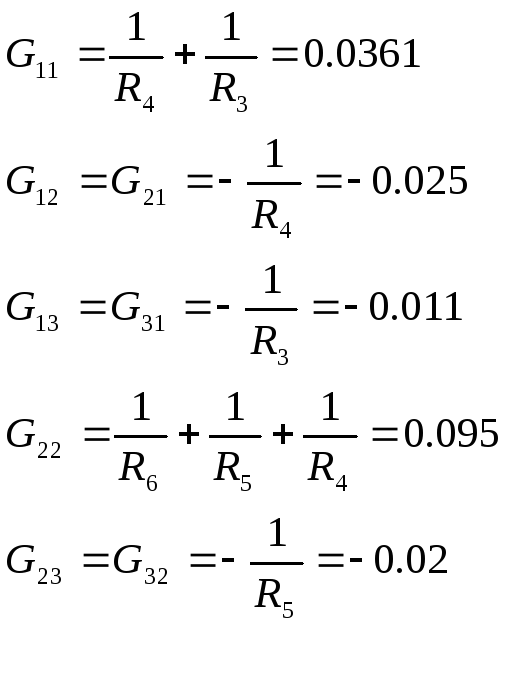
φ₁ = – 445,7591492 В; φ₂ = –255,2890572 В; φ₃ = –155,421301 В; φ₄ = 0 В

U₄₁ = φ₄ – φ₁

U₄₁ = Uxx – U_E1

Uxx = U₄₁ + U_E1= φ₄ – φ₁ + E₁ = 0 – (– 445,7591492) + (–250) = 195,7591492 В

Определим R_ВН эквивалентного генератора. Проведём преобразования схемы.

; ; ;

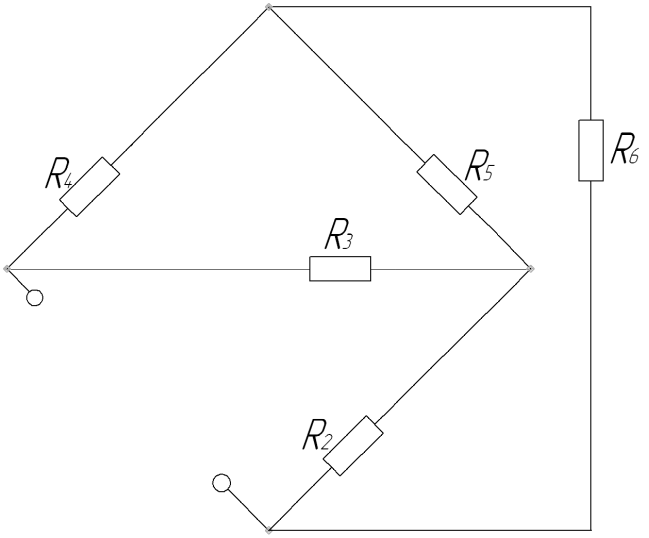
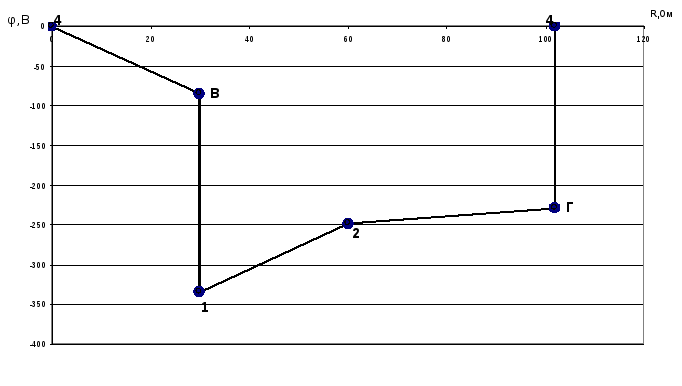
6. Потенциальная диаграмма для контура 1–2–4–1

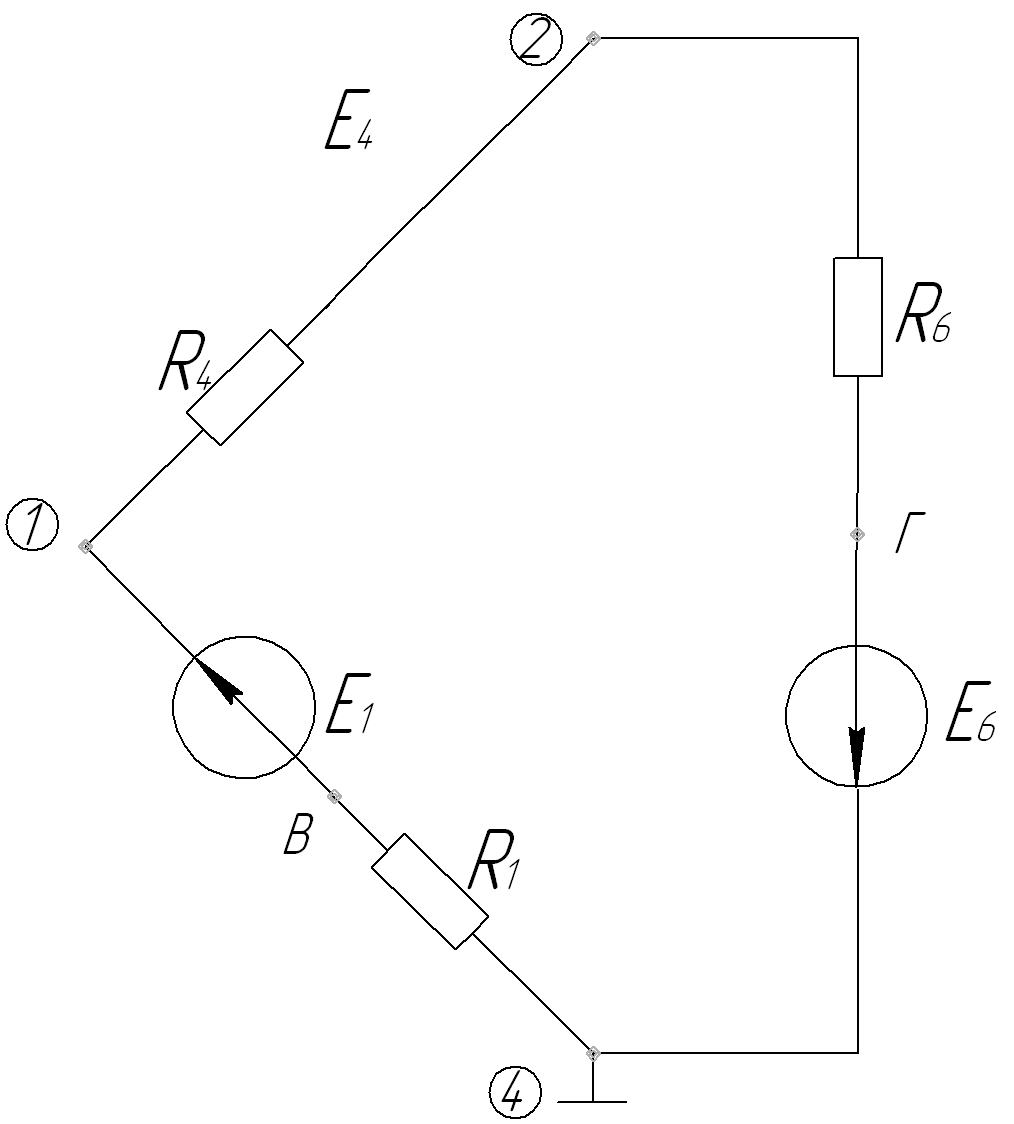
φ₄= 0 В

φ_B = –I₁∙R₁ = –84,45 В

φ₁ = – 334,45 В

φ₂ = – 248,44 В

φ_Г = φ₂ – I₆∙R₆ = –228,662 В